國立中央大學附屬中壢高級中學106學年度第1次教師甄選
一、填充題
解:$$A=\begin{bmatrix} 1 & a & b\\ 0 & 1 & a\\ 0 & 0 & 1\end{bmatrix}=\begin{bmatrix} 1 & 0 & 0\\ 0 & 1 &0\\ 0 & 0 & 1\end{bmatrix} +\begin{bmatrix} 0 & a & b\\ 0 & 0 & a\\ 0 & 0 & 0\end{bmatrix} \equiv I+B \Rightarrow \cases{I^n=I,n\in N\\B^k =0,k\ge 3,k\in Z\\ B^2=\begin{bmatrix} 0 & 0 & a^2\\ 0 & 0 & 0\\ 0 & 0 & 0\end{bmatrix} }\\ \Rightarrow A^{10} = (B+I)^{10} = \sum_{k=0}^{10}C^{10}_kB^kI^{10-k}= \sum_{k=0}^{2}C^{10}_kB^k I^{10-k}= I+10B+45B^2\\ =\begin{bmatrix} 1 & 0 & 0\\ 0 & 1 &0\\ 0 & 0 & 1\end{bmatrix}+\begin{bmatrix} 0 & 10a & 10b\\ 0 & 0 & 10a\\ 0 & 0 & 0\end{bmatrix}+ \begin{bmatrix} 0 & 0 & 45a^2\\ 0 & 0 & 0\\ 0 & 0 & 0\end{bmatrix} =\begin{bmatrix} 1 & 10a & 45a^2+10b\\ 0 & 1 & 10a\\ 0 & 0 & 1\end{bmatrix} \\=\begin{bmatrix} 1 & ka & pa^2+qb\\ 0 & 1 & ka\\ 0 & 0 & 1\end{bmatrix} \Rightarrow \cases{k=10\\ q=10 \\ p=45} \Rightarrow k+p+q=\bbox[red,2pt]{65}$$解:$$\alpha,\beta為x^2+2x-5=0的兩根\Rightarrow \cases{\alpha+\beta =-2\\ \alpha\beta=-5} \Rightarrow \alpha^2+\beta^2=(\alpha+\beta)^2 -2\alpha\beta=14\\ 因此(\alpha+1)(\alpha+2)(\beta +1) (\beta+2)(\alpha^3 +\beta^3) = [(\alpha+1)(\beta +1)][(\alpha+2)(\beta+2) ](\alpha^3 +\beta^3)\\ =(\alpha\beta+\alpha+\beta+1)(\alpha\beta+2(\alpha+\beta) +4)(\alpha+\beta) (\alpha^2-\alpha\beta+\beta^2) \\ =(-5-2+1)(-5-4+4)(-2)(14+5) =(-6)(-5)(-2)(19) = \bbox[red,2pt]{-1140}$$
解:
$$z^5+z-1=0 \Rightarrow z^5=1-z \Rightarrow |z^5|=|1-z| \Rightarrow |1-z|=1\\ 兩式\cases{|z|=1\\ |1-z|=1}之交集,相當於兩圓\cases{x^2+y^2=1\\ (x-1)^2+y^2=1}之交集,即上圖之z_1,z_2\\ \Rightarrow \cases{z_1=\cos { \pi \over 3}+i\sin {\pi\over 3} \\z_2=\cos { -\pi \over 3}+i\sin {-\pi\over 3}} \Rightarrow z=\bbox[red,2pt]{{1\over 2}\pm {\sqrt 3\over 2}i}$$
解:$$\cases{44-8=4(11-2) = 4\cdot 9=2^2\cdot 3^2 = 6^2\\ 4444-88=44(101-2)= 44\cdot 99=2^2\cdot 11^2\cdot 3^2=66^2 \\ 444444-888=444(1001-2) =444\cdot 999 =2^2\cdot 111^2\cdot 3^2 = 666^2\\ \cdots \\\overbrace{4\cdots 4}^{2n個}-\overbrace{8\cdots 8}^{n個} =\overbrace{4\cdots 4}^{n個}(10\cdots 01-2)= \overbrace{4\cdots 4}^{n個}\cdot \overbrace{9\cdots 9}^{n個} =2^2\cdot (1\cdots 1)^2\cdot 3^2 = (\overbrace{6\cdots 6}^{n個})^2} \\ \Rightarrow \sum_{k=1}^n a_k= 6+66 + \cdots + \overbrace{6\cdots 6}^{n個}={6\over 9}(9+99+\cdots + \overbrace{9\cdots 9}^{n個}) ={6\over 9}\left(10 + 10^2+\cdots + 10^n-n\right) \\ ={6\over 9}\left({10^{n+1}-10 \over 9} -n\right) ={2\over 27}10^{n+1}-{6\over 9}n-{20\over 27} ={2\over 27}\left[10^{n+1}-9n-10 \right] \equiv {a\over 27}[10^{n+1}+bn+c]\\ \Rightarrow (a,b,c)= \bbox[red,2pt]{(2,-9,-10)}$$
解:$$\cases{O(0,0)\\ A(4,0)\\ B(0,3)\\ C(2,0)} \Rightarrow \cases{圓\Gamma:(x-2)^2+y^2=4\\ 直線L_1=\overleftrightarrow{AB}:y= -{3\over 4}x+3 \\ 直線L_2= \overleftrightarrow{BC}: y=-{3\over 2}x+3} \Rightarrow \Gamma 與L_1相交於P({36\over 25},{48\over 25}) \\ \Rightarrow L_3=\overleftrightarrow{OP}:y={4\over 3}x \Rightarrow L_2與L_3交於Q({18\over 17},{24\over 17})\Rightarrow \overline{PQ}= \bbox[red,2pt]{54\over 85}$$
解:$$圖形y=x^3+x+1的對稱點為(0,1),又\overline{AB}=\overline{BC} \Rightarrow \cases{B=(0,1)\\ A、C互為對稱點} \\ \Rightarrow L經過B \Rightarrow L: y=mx+1 \Rightarrow A(a,ma+1)\Rightarrow \cases{A在y=x^3+x+1上\\ \overline{AB}=\sqrt 5} \\ \Rightarrow \cases{ma+1=a^3+a+1\\ \sqrt{a^2+(ma)^2}=\sqrt 5} \Rightarrow \cases{m=a^2+1\cdots(1) \\a^2(1+m^2)=5 \cdots(2)} ,將(1)代入(2) \Rightarrow a^6+2a^4+2a^2-5=0 \\ \Rightarrow a^6+2a^4+2a^2-5=(a^2-1)(a^4+3a^2+5)=0 \Rightarrow a^2=1 \Rightarrow m=2 \\ \Rightarrow L:\bbox[red,2pt]{y=2x+1}$$
解:$$\cases{{\sqrt 3\over 2}x^2+{1\over \sqrt 3}y^2 \ge 2\sqrt{{1\over 2}x^2y^2} =\sqrt 2xy \\ {1\over 2\sqrt 3}y^2+{\sqrt 3\over 2}z^2 \ge 2\sqrt{{1\over 4}y^2z^2}=yz},兩式相加 \Rightarrow {\sqrt 3\over 2}(x^2+y^2+z^2) \ge \sqrt 2xy +yz\\ \Rightarrow {\sqrt 3\over 2} \ge \sqrt 2xy+yz \Rightarrow \sqrt 2xy+yz最大值為\bbox[red,2pt]{\sqrt 3\over 2}$$
解:$$三中線為邊長的\triangle 面積={3\over 4}\triangle ABC(公式證明:\href{https://chu246.blogspot.com/2018/10/blog-post.html}{按這裡})={3\over 4}\times 3\sqrt{15}= {9\over 4}\sqrt{15}\\假設三中線長度為3,6,a,令s=(3+6+a)\div 2={a+9\over 2} \\\Rightarrow 三中線為邊長的\triangle 面積= \sqrt{s(s-3)(s-6)(s-a)} = \sqrt{{a+9\over 2} \cdot {a+3\over 2} \cdot {a-3\over 2} \cdot {9-a\over 2}} \\= {1\over 4}\sqrt{(81-a^2)(a^2-9)} ={9\over 4}\sqrt{15} \Rightarrow (81-a^2)(a^2-9)=81\times 15 \Rightarrow a^4-90a^2+1944=0 \\ \Rightarrow \cases{a^2=54\\ a^2=36} \Rightarrow 最大的a= \bbox[red,2pt]{3\sqrt 6}(\because 3\sqrt 6\gt 6) $$
解:$$由於圖形的對稱性,我們可以假設\cases{E[A_1\to A_6]=E_1\\ E[A_4\to A_6]=E_1\\ E[A_2\to A_6]=E_2 \\ E[A_3\to A_6]=E_3 \\E[A_5\to A_6]=E_3} ;\\因此\cases{E_3 = {1\over 4}((E[A_1\to A_6]+1) +(E[A_2\to A_6]+1) + (E[A_5\to A_6]+1)+ 1) \\ E_2= {1\over 4}((E[A_1\to A_6]+1) +(E[A_3\to A_6]+1) +(E[A_4\to A_6]+1) +(E[A_5\to A_6]+1)) \\ E_1={1\over 2}((E[A_2\to A_6]+1) +(E[A_3\to A_6]+1))} \\ \Rightarrow \cases{E_3={1\over 4}(E_1+E_2+E_3)+1\cdots(1) \\ E_2={1\over 4}(E_1+E_3+E_1+ E_3+4)={1\over 2}(E_1+E_3)+1 \cdots(2)\\ E_1={1\over 2}(E_2+ E_3)+1\cdots(3)}\\ 將(2)代入(1)及(3) \Rightarrow \cases{E_3={3\over 5}E_1+2\\ E_3=E_1-2} \Rightarrow {3\over 5}E_1+2 =E_1-2 \Rightarrow {2\over 5}E_1=4 \Rightarrow E_1= \bbox[red,2pt]{10}$$
解:$$(\sqrt 2+\sqrt 3)^{2016} =((\sqrt 2+\sqrt 3)^2)^{1008} = (5+2\sqrt 6)^{1008}\\ 令\cases{a=5+2\sqrt 6\\ b=5-2\sqrt 6}
\Rightarrow \cases{a+b=10\\ ab=1} \Rightarrow a^2+b^2=(a+b)^2-2ab=98\\ a^n+b^n=(a+b)(a^{n-1}+b^{n-1})-ab(a^{n-2}+b^{n-2}) =10(a^{n-1}+b^{n-1})-(a^{n-2}+b^{n-2}) \\ \Rightarrow (a^n+b^n) \mod 10= -(a^{n-2}+b^{n-2}) \mod 10 \\ \Rightarrow \cases{(a+b) \mod 10=0\\ (a^2+b^2) \mod 10= -2=8\\ (a^3+b^3) \mod 10=0 \\ (a^4+b^4) \mod 10=-8 =2 \\ (a^5+b^5) \mod 10=0\\ \cdots } \Rightarrow \cases{(a^{4k}+b^{4k}) \mod 4=2\\ (a^{4k+1}+b^{4k+1}) \mod 4=0\\(a^{4k+2}+b^{4k+2}) \mod 4=8\\ (a^{4k+3}+b^{4k+3}) \mod 4=0},k=0,1,2,...\\ \Rightarrow (a^{1008}+b^{1008}) \mod 10 =(a^{4\cdot 252}+b^{4\cdot 252}) \mod 10 = 2 \\ \Rightarrow ((5+2\sqrt 6)^{1008} +(5-2\sqrt 6)^{1008}) \mod 10 =2 \\ 由於(5-2\sqrt 6)^{1008}近乎0,但不為0,因此(5+2\sqrt 6)^{1008}的個位數為1,小數點第1位為9\\,即(a,b)=\bbox[red,2pt]{(1,9)}$$
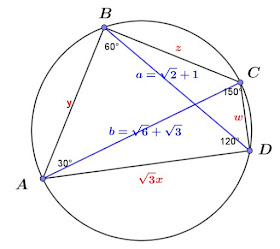
$$\cases{3x^2+y^2-3xy=3+2\sqrt 2 =(\sqrt 2+1)^2 \equiv a^2\\ y^2+ z^2-yz=9 +6 \sqrt 2= (\sqrt 6+\sqrt 3)^2\equiv b^2 \\ z^2+w^2+\sqrt 3zw =3+2\sqrt 2=(\sqrt 2+1)^2 \equiv a^2\\ w^2+3x^2+\sqrt 3wx =9+6\sqrt 2= (\sqrt 6+\sqrt 2)^2\equiv b^2} \\ \Rightarrow \cases{{(\sqrt 3x)^2+y^2-a^2 \over 2\sqrt 3xy} ={\sqrt 3\over 2} =\cos 30^\circ \\ { y^2+z^2-b^2 \over 2yz} ={1\over 2} =\cos 60^\circ \\ {z^2+w^2-a^2\over 2zw}=-{\sqrt 3\over 2} =\cos 150^\circ \\ {w^2+(\sqrt 3x)^2-b^2\over 2\sqrt 3wx}=-{1\over 2} =\cos 120^\circ},剛好\cases{30^\circ +60^\circ + 150^\circ + 120^\circ=360^\circ \\ 30^\circ + 150^\circ= 60^\circ+120^\circ =180^\circ}$$
$$因此我們可以假設有一圓內接矩形,其邊長分別為\sqrt 3x、y、z、w,兩對角線長為a及b;\\矩形各頂點角度就是30^\circ,60^\circ, 150^\circ,120^\circ ,如上圖;\\由托勒密定理(\href{https://chu246.blogspot.com/2020/11/ptolemys-theorem.html}{按這裡}): 圓內接矩形,兩對角線長之積 =兩對邊積之和;\\ 也就是\sqrt 3xz +yw = ab = (\sqrt 2+1)(\sqrt 6+\sqrt 3) = \bbox[red,2pt]{3\sqrt 3+2\sqrt 6}$$二、 計算證明題
解:$$\log_{0.5}(x^2-2x-15) > \log_{0.25}(x+13)^2 = \log_{0.5}(x+13) \Rightarrow x^2-2x-15 < x+13 \\ \Rightarrow x^2-3x-28 < 0 \Rightarrow (x-7)(x+4) < 0 \Rightarrow -4 < x < 7 \cdots(1)\\ 又x^2-2x-15 > 0 \Rightarrow (x-5)(x+3) > 0 \Rightarrow x > 5或 x< -3 \cdots(2)\\再加上\cos 2x \ge 0 \Rightarrow -\pi/2 \pm 2k\pi \le 2x \le \pi/2 \pm 2k\pi \Rightarrow -\pi/4\pm k\pi \le x \le \pi/4 \pm k\pi\cdots(3)\\ 條件(1) \cap 條件(2) \cap 條件(3) \Rightarrow \bbox[red,2pt]{-5\pi/4 \le x < -3或 7\pi/4 \le x < 7}$$解:
(1)$$\cases{y^2=-x\\ y=k(x+1)},求交集\Rightarrow y^2=-({y\over k}-1) \Rightarrow y^2+{1\over k}y-1=0 \Rightarrow \cases{y_1+y_2= -1/k \\ y_1y_2=1}\\ \Rightarrow 兩交點為\cases{A(-y_1^2,y_1)\\ B(-y_2^2,y_2)} \Rightarrow \overrightarrow{OA} \cdot \overrightarrow{OB} =y_1^2y_2^2 +y_1y_2 =1-1=0 \Rightarrow \overline{OA} \bot \overline{OB},\bbox[red, 2pt]{故得證}$$(2)$$\triangle OAB = {1\over 2}\overline{OA}\cdot \overline{OB}= \sqrt{10} \Rightarrow \sqrt{y_1^4+y_1^2} \cdot \sqrt{y_2^4+y_2^2} =\sqrt{40} \\ \Rightarrow (y_1y_2)^4+ y_1^2y_2^2(y_1^2+y_2^2) +(y_1y_2)^2 =40 \Rightarrow 2+({1\over k^2}+2)=40 \Rightarrow {1\over k^2}=36 \\ \Rightarrow k=\bbox[red,2pt]{\pm {1\over 6}}\\ 註: y_1^2+y_2^2 =(y_1+y_2)^2-2y_1y_2= {1\over k^2}+2$$
解:$$將\cases{x+y+z=3 \\ x^3+y^3+z^3=3}\text{代入 } x^3+y^3+z^3-3xyz =(x+y+z)((x+y+z)^2 -3(xy+yz+zx))\\ \Rightarrow 3-3xyz= 3(9-3(xy+yz+zx)) \Rightarrow xyz-3(xy+yz+zx) =-8 \\ \Rightarrow xyz-3(xy+yz+zx)+ \color{blue}{9(x+y+z)-27} =-8 \Rightarrow (x-3)(y-3)(z-3)=-8\\ 因此我們有\cases{(x-3) +(y-3)+(z-3) =-6 \\ (x-3)(y-3)(z-3)=-8},由於x,y,z皆為整數,符合該二條件的解只有:\\ (x-3,y-3,z-3) =(-2,-2,-2) 或 (1,1,-8)的排列\\ \Rightarrow (x,y,z)=(4,4,-5)的排列 ((1,1,1)不合題意)\\ \Rightarrow x^2+y^2+z^2 =4^2+4^2 +5^2= \bbox[red,2pt]{57}$$
解:$$將\cases{x+y+z=3 \\ x^3+y^3+z^3=3}\text{代入 } x^3+y^3+z^3-3xyz =(x+y+z)((x+y+z)^2 -3(xy+yz+zx))\\ \Rightarrow 3-3xyz= 3(9-3(xy+yz+zx)) \Rightarrow xyz-3(xy+yz+zx) =-8 \\ \Rightarrow xyz-3(xy+yz+zx)+ \color{blue}{9(x+y+z)-27} =-8 \Rightarrow (x-3)(y-3)(z-3)=-8\\ 因此我們有\cases{(x-3) +(y-3)+(z-3) =-6 \\ (x-3)(y-3)(z-3)=-8},由於x,y,z皆為整數,符合該二條件的解只有:\\ (x-3,y-3,z-3) =(-2,-2,-2) 或 (1,1,-8)的排列\\ \Rightarrow (x,y,z)=(4,4,-5)的排列 ((1,1,1)不合題意)\\ \Rightarrow x^2+y^2+z^2 =4^2+4^2 +5^2= \bbox[red,2pt]{57}$$





你好:請問a=6為什麼不符合兩邊和大於第三邊呢?
回覆刪除已修訂,謝謝指正!
刪除