解： 直線L:y=−14x+7⇒斜率=−14、x截距=28、7+4×7≠28，故選(B)。
解： x=4y2+8y⇒(y+1)2=14(x+4)⇒頂點在(−4,−1)，故選(B)。
解： \left( A \right) \sin { 885° } =\sin { \left( 885°-360\times 2 \right) } =\sin { 165° } =\sin { 15° } \\ \left( B \right) \cos { \left( -430° \right) } =\cos { \left( -430°+360\times 2 \right) } =\cos { 290° } =\cos { 70° } \\ \left( C \right) \tan { 131° } =-\tan { 49° } <-1\\ \left( D \right) \sin { \left( -2010° \right) } =\sin { \left( -2010°+360\times 6 \right) } =\sin { 150° } =\sin { 30° } ，故選\bbox[red,2pt]{(C)} 。
解： 令A=(0,0)\Rightarrow B=(4,8)、D=(1,4)、C=(4+1,8+4)=(5,12)\\ \Rightarrow \left|\overrightarrow{AC}\right| +\left|\overrightarrow{BD}\right| =\sqrt{5^2+12^2}+ \sqrt{3^2+4^2}=13+5=18，故選\bbox[red,2pt]{(B)} 。
解：\begin{cases} L_{ 1 }:x+3y-2=0 \\ L_{ 2 }:3x+y+2=0 \end{cases}\Rightarrow \begin{cases} 3x+9y-6=0 \\ 3x+y+2=0 \end{cases}\Rightarrow 8y-8=0\Rightarrow y=1,x=-1\\ L_{ 3 }:x-y-2=0斜率=1\Rightarrow 過A(-1,1)且斜率為1的直線:x-y+2=0\\ \Rightarrow 不通過第四象限 ，故選\bbox[red,2pt]{(D)} 。
解：圓C:{ \left( x+1 \right) }^{ 2 }+{ \left( y-2 \right) }^{ 2 }={ 3 }^{ 2 }\Rightarrow 圓心(-1,2),半徑3\\ 圓心至直線L:3x+4y+5=0的距離=\left| \frac { -3+8+5 }{ \sqrt { { 3 }^{ 2 }+{ 4 }^{ 2 } } } \right| =2=b\\ 圓心至直線L的距離小於半徑\Rightarrow 圓與直線交點=2=a ，故選\bbox[red,2pt]{(C)} 。
解：\log _{ 9 }{ \left( 10{ x }^{ 2 }-6x+5 \right) } -\log _{ 3 }{ x } -1=0\Rightarrow \log _{ 9 }{ \left( 10{ x }^{ 2 }-6x+5 \right) } -\log _{ 9 }{ x^{ 2 } } -\log _{ 9 }{ 9 } =0\\ \Rightarrow \log _{ 9 }{ \frac { 10{ x }^{ 2 }-6x+5 }{ 9x^{ 2 } } } =0\Rightarrow \frac { 10{ x }^{ 2 }-6x+5 }{ 9x^{ 2 } } =1\Rightarrow { x }^{ 2 }-6x+5\Rightarrow (x-5)(x-1)=0\\ \Rightarrow p+q=5+1=6\Rightarrow \frac { 1 }{ p+q } =\frac { 1 }{ 6 } ，故選\bbox[red,2pt]{(A)} 。
解： 前鋒4人選2人有C_2^4種選法、中鋒3人選1人有C_1^3種選法、\\後衛有5人選2人有C_2^5種選法，共有C_2^4\times C_1^3\times C_2^5 = 6\times 3\times 10=180，\\故選\bbox[red,2pt]{(C)} 。
解： 假設全校有a人\Rightarrow 各年級分別有0.4a、0.32a及0.28a人\\ \Rightarrow 各年級女生人數分別為0.4a\times 0.5、0.32a\times 0.4及0.28a\times 0.6\\ \Rightarrow 女生共有0.2a+0.128a+0.168a =0.496a人\\ \Rightarrow 任取一人為女生的機率=\frac{0.496}{a}=49.6 \%，故選\bbox[red,2pt]{(D)} 。
解：
解： x+y\ge10不含原點，所以該區域在A及B\\x-y\le1 包含原點，所以該區在B、C\\ \Rightarrow 兩區域取交集，故選\bbox[red,2pt]{(B)} 。
解： (C)應該是\int _{ a }^{ c }{ f\left( x \right) dx } =\int _{ a }^{ b }{ f\left( x \right) dx } +\int _{ b }^{ c }{ f\left( x \right) dx } ，故選\bbox[red,2pt]{(C)} 。
解： 投骰子不是出現奇數就是偶數點，因此出現奇數的機率為\frac{2}{3}，出現偶數的機率為\frac{1}{3}，\\出現奇數的期望值=10\times\frac{2}{3}=\frac{20}{3}\\出現偶數的期望值=40\times\frac{1}{3}=\frac{40}{3}\\兩期望值之和=\frac{60}{3}=20，故選\bbox[red,2pt]{(B)}。
解： 已知\triangle 三邊長分別a,b,c且令s=(a+b+c)\div 2，則其外接圓半徑\\r=\frac{abc}{4\sqrt{s(s-a)(s-b)(s-c)}}=\frac{4\times 6\times 8}{4\sqrt{9\times 5\times 3\times 1}} =\frac{48}{\sqrt{135}}\\ =\frac{16}{\sqrt{15}}\Rightarrow 圓面積=\frac{256}{15}\pi，故選\bbox[red,2pt]{(A)} 。
解：\left( A \right) f\left( x \right) =\left( 4x+5 \right) \left( 6x+7 \right) \Rightarrow f^{ ' }\left( x \right) =4\left( 6x+7 \right) +6\left( 4x+5 \right) =48x+58\\ \left( B \right) f\left( x \right) =\sqrt [ 3 ]{ { x }^{ 7 } } +4x={ x }^{ \frac { 7 }{ 3 } }+4x\Rightarrow f^{ ' }\left( x \right) =\frac { 7 }{ 3 } { x }^{ \frac { 4 }{ 3 } }+4\\ \left( C \right) f\left( x \right) ={ \left( 4x+5 \right) }^{ 2 }\Rightarrow f^{ ' }\left( x \right) =2\left( 4x+5 \right) \times 4=8\left( 4x+5 \right) \\ \left( D \right) f\left( x \right) =\frac { 4x+4 }{ x+1 } =\frac { 4(x+1) }{ x+1 } =4\Rightarrow f^{ ' }\left( x \right) =0 ，\\故選\bbox[red,2pt]{(B)} 。
解：\left( A \right) \lim _{ n\rightarrow \infty }{ \frac { { 3 }^{ n }-{ 2 }^{ n } }{ { 5 }^{ n } } } =\lim _{ n\rightarrow \infty }{ \left[ { \left( \frac { 3 }{ 5 } \right) }^{ n }-{ \left( \frac { 2 }{ 5 } \right) }^{ n } \right] } =0\\ \left( C \right) \lim _{ n\rightarrow \infty }{ \frac { 0.01n }{ 5n-1 } } =\frac { 0.01 }{ 5 } \\ \left( D \right) \lim _{ n\rightarrow \infty }{ \left( n-\sqrt { { n }^{ 2 }-1 } \right) } =\lim _{ n\rightarrow \infty }{ \left( \frac { \left( n-\sqrt { { n }^{ 2 }-1 } \right) \left( n+\sqrt { { n }^{ 2 }-1 } \right) }{ n+\sqrt { { n }^{ 2 }-1 } } \right) } \\=\lim _{ n\rightarrow \infty }{ \left( \frac { 1 }{ n+\sqrt { { n }^{ 2 }-1 } } \right) } =0 ，\\故選\bbox[red,2pt]{(B)} 。
解： f\left( x \right) =a{ x }^{ 3 }+b{ x }^{ 2 }+cx+d=p(x)\left( { x }^{ 2 }-1 \right) =q(x)\left( x-2 \right) +6\\ \begin{cases} f\left( 1 \right) =0\Rightarrow a+b+c+d=0 \\ f\left( -1 \right) =0\Rightarrow -a+b-c+d=0 \end{cases}\Rightarrow \begin{cases} b+d=0 \\ a+c=0 \end{cases}\\ f\left( 2 \right) =6\Rightarrow 8a+4b+2c+d=6\Rightarrow 6a+2(a+c)+3b+(b+d)=6\\ \Rightarrow 6a+3b=6\Rightarrow 3(2a+b)=6\Rightarrow 2a+b=2，故選\bbox[red,2pt]{(C)} 。
解： 2{ \left( 1+i \right) }^{ 2 }+k(1+i)+6+2i=0\Rightarrow 4i+k(1+i)+6+2i=0\\ \Rightarrow 6(1+i)+k(1+i)=0\Rightarrow k=-6，故選\bbox[red,2pt]{(A)} 。
解： S=1+\frac { 1 }{ 3 } +\frac { 1 }{ { 2 }^{ 2 } } +\frac { 1 }{ { 3 }^{ 3 } } +\frac { 1 }{ { 2 }^{ 4 } } +\frac { 1 }{ { 3 }^{ 5 } } +\cdots +\frac { 1 }{ { 2 }^{ 2k } } +\frac { 1 }{ { 3 }^{ 2k+1 } } +\cdots \\ =\left[ 1+\frac { 1 }{ { 2 }^{ 2 } } +\frac { 1 }{ { 2 }^{ 4 } } +\cdots +\frac { 1 }{ { 2 }^{ 2k } } +\cdots \right] +\left[ \frac { 1 }{ 3 } +\frac { 1 }{ { 3 }^{ 3 } } +\frac { 1 }{ { 3 }^{ 5 } } +\cdots +\frac { 1 }{ { 3 }^{ 2k+1 } } +\cdots \right] \\ =\left[ \frac { 1 }{ 1-\frac { 1 }{ { 2 }^{ 2 } } } \right] +\left[ \frac { \frac { 1 }{ 3 } }{ 1-\frac { 1 }{ { 3 }^{ 2 } } } \right] =\frac { 4 }{ 3 } +\frac { 3 }{ 8 } =\frac { 41 }{ 24 } ，故選\bbox[red,2pt]{(A)} 。
解： { 5 }^{ r }=4{ \left( \sqrt [ 3 ]{ 40 } +\frac { \sqrt [ 3 ]{ 5 } }{ 2 } \right) }^{ 2 }\Rightarrow \frac { { 5 }^{ r } }{ 4 } ={ \left( \sqrt [ 3 ]{ 40 } +\frac { \sqrt [ 3 ]{ 5 } }{ 2 } \right) }^{ 2 }\\ \Rightarrow \log { \left( \frac { { 5 }^{ r } }{ 4 } \right) } =2\log { { \left( \sqrt [ 3 ]{ 40 } +\frac { \sqrt [ 3 ]{ 5 } }{ 2 } \right) } } =2\log { { \left( 2\sqrt [ 3 ]{ 5 } +\frac { \sqrt [ 3 ]{ 5 } }{ 2 } \right) } } =2\log { { \left( \frac { 5 }{ 2 } \sqrt [ 3 ]{ 5 } \right) } } \\ \Rightarrow r\log { 5 } -2\log { 2 } =2\log { { \left( { 5 }^{ \frac { 4 }{ 3 } } \right) } } -2\log { 2 } =\frac { 8 }{ 3 } \log { 5 } -2\log { 2 } \Rightarrow r=\frac { 8 }{ 3 } ，故選\bbox[red,2pt]{(A)} 。
解：
解：
解： 令A=(0,0),B=(x_{ b },y_{ b }),C=(x_{ c },y_{ c }),則D=\left( \frac { x_{ b }+x_{ c } }{ 2 } ,\frac { y_{ b }+y_{ c } }{ 2 } \right) \\ \overrightarrow { AD } \cdot \overrightarrow { BC } =\left( \frac { x_{ b }+x_{ c } }{ 2 } ,\frac { y_{ b }+y_{ c } }{ 2 } \right) \cdot \left( x_{ c }-x_{ b },y_{ c }-y_{ b } \right) \\ =\frac { 1 }{ 2 } \left( x_{ b }+x_{ c } \right) \left( x_{ c }-x_{ b } \right) +\frac { 1 }{ 2 } \left( y_{ b }+y_{ c } \right) \left( y_{ c }-y_{ b } \right) \\ =\frac { 1 }{ 2 } \left( x_{ c }^{ 2 }-x_{ b }^{ 2 } \right) +\frac { 1 }{ 2 } \left( y_{ c }^{ 2 }-y_{ b }^{ 2 } \right) =\frac { 1 }{ 2 } \left[ \left( x_{ c }^{ 2 }+y_{ c }^{ 2 } \right) -\left( x_{ b }^{ 2 }+y_{ b }^{ 2 } \right) \right] \\ =\frac { 1 }{ 2 } \left[ { \overline { AC } }^{ 2 }-{ \overline { AB } }^{ 2 } \right] =\frac { 1 }{ 2 } \left( 25-81 \right) =-28，故選\bbox[red,2pt]{(A)} 。
解： 1+i為f之一根，1-i亦是另一根，因此1,1+i,1-i為f之三根\\ \Rightarrow f(x)=a(x-1)(x^2-x+2)又 f(0)>0\Rightarrow a\times(-1)\times 2>0\Rightarrow a<0\\(A)f(-2)=-24a>0 \\(B)f(2)=4a<0 \\(C)f(4)=42a<0 \\(D)f(6)=160a<0，\\故選\bbox[red,2pt]{(C)} 。
解： f\left( x \right) =\left( \cos { x } +3\sin { x } \right) \left( \cos { x } -\sin { x } \right) =\cos ^{ 2 }{ x } +2\sin { x } \cos { x } -3\sin ^{ 2 }{ x } \\ =\cos ^{ 2 }{ x } +2\sin { x } \cos { x } -3\left( 1-\cos ^{ 2 }{ x } \right) =4\cos ^{ 2 }{ x } +2\sin { x } \cos { x } -3\\ =2\left( 2\cos ^{ 2 }{ x } -1 \right) +2\sin { x } \cos { x } -1=2\cos { 2x } +\sin { 2x } -1\\ =\sqrt { 5 } \left( \frac { 2 }{ \sqrt { 5 } } \cos { 2x } +\frac { 1 }{ \sqrt { 5 } } \sin { 2x } \right) -1=\sqrt { 5 } \left( \sin { \alpha } \cos { 2x } +\cos { \alpha } \sin { 2x } \right) -1\\ =\sqrt { 5 } \sin { \left( \alpha +2x \right) } -1\Rightarrow -\sqrt { 5 } -1\le f\left( x \right) \le \sqrt { 5 } -1，故選\bbox[red,2pt]{(D)} 。
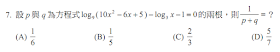
12. (D) n ≠ -1
回覆刪除