105年特種考試地方政府公務人員考試--微積分詳解

105年特種考試地方政府公務人員考試

等 別： 四等考試
類 科：天文
科 目：微積分

微積分 詳解

解：
(一)$$\lim _{ x\to 1^{ + } }{ \left( \frac { 1 }{ \ln { x }  } -\frac { 1 }{ x-1 }  \right)  } =\lim _{ x\to 1^{ + } }{ \left( \frac { x-\ln { x-1 }  }{ \left( x-1 \right) \ln { x }  }  \right)  } =\lim _{ x\to 1^{ + } }{ \left( \frac { 1-\frac { 1 }{ x }  }{ \ln { x } +\frac { x-1 }{ x }  }  \right)  } \\ =\lim _{ x\to 1^{ + } }{ \left( \frac { 1-\frac { 1 }{ x }  }{ \ln { x } +1-\frac { 1 }{ x }  }  \right)  } =\lim _{ x\to 1^{ + } }{ \left( \frac { \frac { 1 }{ x^{ 2 } }  }{ \frac { 1 }{ x } +\frac { 1 }{ x^{ 2 } }  }  \right)  } =\frac { 1 }{ 1+1 } =\bbox[red,2pt]{\frac { 1 }{ 2 }} $$
(二)$$\frac { d^{ 3 } }{ dx } \ln { \left| 2x+1 \right|  } =\frac { d^{ 2 } }{ dx } \frac { 2 }{ 2x+1 } =\frac { d }{ dx } \frac { -4 }{ \left( 2x+1 \right) ^{ 2 } } =\bbox[red,2pt]{\frac { 16 }{ \left( 2x+1 \right) ^{ 3 } } }$$

---

解：

(一)$$\frac { 5x^{ 2 }+20x+6 }{ x^{ 3 }+2x^{ 2 }+x } =\frac { 5x^{ 2 }+20x+6 }{ x\left( x+1 \right) ^{ 2 } } =\frac { A }{ x } +\frac { B }{ x+1 } +\frac { C }{ \left( x+1 \right) ^{ 2 } } \\ \Rightarrow A\left( x+1 \right) ^{ 2 }+Bx\left( x+1 \right) +Cx=5x^{ 2 }+20x+6\\ \begin{cases} x=0 \\ x=-1 \\ x=1 \end{cases}\Rightarrow \begin{cases} A=6 \\ C=9 \\ 4A+2B+C=31 \end{cases}\Rightarrow \begin{cases} A=6 \\ C=9 \\ B=-1 \end{cases}\\ \Rightarrow \int { \frac { 5x^{ 2 }+20x+6 }{ x^{ 3 }+2x^{ 2 }+x } dx } =\int { \frac { 6 }{ x } dx } -\int { \frac { 1 }{ x+1 } dx } +\int { \frac { 9 }{ \left( x+1 \right) ^{ 2 } } dx } \\ =\bbox[red,2pt]{6\ln { \left| x \right|  } -\ln { \left| x+1 \right|  } -\frac { 9 }{ x+1 } +C}$$
(二)$$\int _{ 0 }^{ \pi  }{ \int _{ 0 }^{ \sin { x }  }{ \left( 1+\cos { x }  \right)  } dydx } =\int _{ 0 }^{ \pi  }{ \sin { x } \left( 1+\cos { x }  \right) dx } =\int _{ 0 }^{ \pi  }{ \left( \sin { x } +\sin { x\cos { x }  }  \right) dx } \\ =\int _{ 0 }^{ \pi  }{ \left( \sin { x } +\frac { 1 }{ 2 } \sin { 2x }  \right) dx } =\left. \left[ -\cos { x } -\frac { 1 }{ 4 } \cos { 2x }  \right]  \right| ^{ \pi  }_{ 0 }=\left( 1-\frac { 1 }{ 4 }  \right) -\left( -1-\frac { 1 }{ 4 }  \right) \\ =\frac { 3 }{ 4 } +\frac { 5 }{ 4 } =\bbox[red,2pt]{2}$$

---

解：

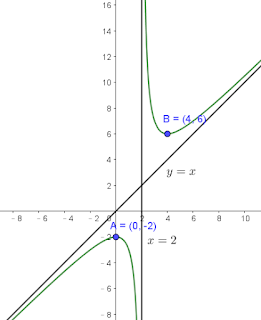
$$f\left( x \right) =\frac { x^{ 2 }-2x+4 }{ x-2 } =x+\frac { 4 }{ x-2 } \Rightarrow \begin{cases} y=x為斜漸近線 \\ x=2為垂直漸近線 \end{cases}\\ 令f'\left( x \right) =0\Rightarrow 1-\frac { 4 }{ { \left( x-2 \right)  }^{ 2 } } =\frac { x\left( x-4 \right)  }{ { \left( x-2 \right)  }^{ 2 } } =0\Rightarrow x=0,x=4\\ f''\left( x \right) =\frac { 8 }{ { \left( x-2 \right)  }^{ 3 } } \Rightarrow \begin{cases} f''\left( 0 \right) =-1<0 \\ f''\left( 4 \right) =1>0 \end{cases}\Rightarrow \begin{cases} f\left( 0 \right) =-2為極大值 \\ f\left( 4 \right) =6為極小值 \end{cases}$$答：極大點為A(0,-2)、極小點為B(4,6)、沒有反曲點，漸近線有兩條，分別為y=x及x=2，圖形如上。

---

解：
$$f\left( x,y \right) =-x^{ 3 }-2y^{ 2 }+4xy+1\Rightarrow \begin{cases} f_{ x }=-3x^{ 2 }+4y \\ f_{ y }=-4y+4x \\ f_{ xx }=-6x \\ f_{ yy }=-4 \\ f_{ xy }=4 \end{cases}\\ \begin{cases} f_{ x }=0 \\ f_{ y }=0 \end{cases}\Rightarrow \begin{cases} -3x^{ 2 }+4y=0 \\ -4y+4x=0 \end{cases}\Rightarrow \left( x,y \right) =\left( 0,0 \right) ,\left( \frac { 4 }{ 3 } ,\frac { 4 }{ 3 }  \right) \\ d=f_{ xx }f_{ yy }-f^{ 2 }_{ xy }=24x-16\Rightarrow \begin{cases} d\left( 0,0 \right) =-16<0 \\ d\left( \frac { 4 }{ 3 } ,\frac { 4 }{ 3 }  \right) =16>0 \\ f_{ xx }\left( \frac { 4 }{ 3 } ,\frac { 4 }{ 3 }  \right) =-8<0 \end{cases}\Rightarrow \begin{cases}\bbox[red,2pt]{\left( 0,0 \right) 為鞍點 }\\\bbox[red,2pt]{ \left( \frac { 4 }{ 3 } ,\frac { 4 }{ 3 }  \right) 為極大點} \end{cases}$$

---

考選部未公布答案，解題僅供參考