103 年高中高職特色招生考試數學科參考題本
由於\(\overset { \frown }{ AB } =\overset { \frown }{ BC } =\overset { \frown }{ CD } =\overset { \frown }{ DE } =\overset { \frown }{ EA } \),所以五邊形ABCDE是一個正五邊形,經過圓心及頂點的直線都是對稱軸,故選\(\bbox[red,2pt]{(A)}\)
解:
$$-\left( x+4 \right) +15\ge 3x-9\Rightarrow -x-4+15\ge 3x-9\Rightarrow -x+11\ge 3x-9\\ \Rightarrow 11+9\ge3x+x\Rightarrow 20\ge4x\Rightarrow 5\ge x,故選\bbox[red,2pt]{(B)}$$
解:3號球有6顆,全部有8+7+6=21顆,因此抽中3號球的機率為\(\frac{6}{21}=\frac{2}{7}\),故選\(\bbox[red,2pt]{(C)}\)
解:$$4x^{ 2 }+3x-16=g\left( x \right) \left( x+2 \right) -6\Rightarrow g\left( x \right) \left( x+2 \right) =4x^{ 2 }+3x-10\\ \Rightarrow g\left( x \right) =\frac { 4x^{ 2 }+3x-10 }{ x+2 } =4x-5,故選\bbox[red,2pt]{(A)} $$
正方形木板的寬度為\(6\times 2=12\)公分,長方形的寬度需為12的因數,因此不可能為9公分,故選\(\bbox[red,2pt]{(C)}\)
解:$$27.6^{ 2 }-4\times 3.8^{ 2 }=27.6^{ 2 }-2^{ 2 }\times 3.8^{ 2 }=27.6^{ 2 }-\left( 2\times 3.8 \right) ^{ 2 }=27.6^{ 2 }-7.6^{ 2 }\\ =\left( 27.6+7.6 \right) \left( 27.6-7.6 \right) =35.2\times 20=704 ,故選\bbox[red,2pt]{(D)}$$
解:$$\overset { { \frown } }{ ABC } +\overset { { \frown } }{ ADC } =7\pi +11\pi =18\pi =圓周長\\ \angle BAD=80°\Rightarrow \angle BCD=180°-80°=100°\Rightarrow \overset { { \frown } }{ BAD } =\frac { 100° }{ 180° } \times 18\pi =10\pi ,故選\bbox[red,2pt]{(C)}$$
解:$$4.3^2=18.49,4.4^2=19.36,故選\bbox[red,2pt]{(B)}$$
解:$$x^{ 2 }+ax-16=\left( x-\alpha \right) \left( x-\beta \right) \Rightarrow \begin{cases} \alpha \beta =-16 \\ \alpha +\beta =-a \end{cases}\\ a是2位數\Rightarrow \alpha ,\beta 其中之一是2位數\Rightarrow 16=16\times 1\left( 16的因數中只有16是2位數 \right) \\ \Rightarrow x^{ 2 }+ax-16=\left( x+1 \right) \left( x-16 \right) \Rightarrow a=-15\Rightarrow 個位數與十位數相差5-1=4,故選\bbox[red,2pt]{(C)}$$
解:
以社團人數取代原比例數字,表(一)變成下表:
舞蹈社 溜冰社 魔術社
上學期 3/12 4/12 5/12
下學期 4/9 3/9 2/9
因此溜冰社: 4/12=1/3=3/9 不變、舞蹈社 3/12=0.25→4/9=0.44 人數變多,故選\(\bbox[red,2pt]{(D)}\)
解:
作\(\overline{FG}\bot\overline{BC}\),及\(\overline{FH}\bot\overline{AE}\),如上圖。
由於\(\overline{EF}\)是\(\angle AEC\)的角平分線,所以\(\triangle FEH\)與\(\triangle FEG\)全等。
令\(\overline{FD}=a\Rightarrow \overline{GC}=a\Rightarrow \overline{EG}=8-a=\overline{EH}\);
又直角\(\triangle ABE\)中: \({\overline{AE}}^2={\overline{AB}}^2+{\overline{BE}}^2 = 6^2+8^2=100 \Rightarrow \overline{AE}=10\),因此\(\overline{AH}=\overline{AE}- \overline{HE} = 10-(8-a)= 2+a\);
又直角\(\triangle AHF\)中: \({\overline{AF}}^2={\overline{AH}}^2+{\overline{HF}}^2 \Rightarrow (16-a)^2=(a+2)^2+6^2 \Rightarrow a=6\),故選\(\bbox[red,2pt]{(C)}\)
解:
\(\triangle ABC\)與\(\triangle EDB\)全等,理由如下:
\(\overline{AC}=\overline{EB}=9, \overline{AB}=\overline{ED}=7, \overline{BC}=\overline{DB}=6\),符合SSS條件,所以兩三角形全等;
因此\(\angle A=\angle E=\alpha\)且\(\angle ACB=\angle DBC=\beta\),在\(\triangle ABC\)中,\(\angle ABD = 180^\circ-\angle A-\angle ACB-\angle DBC=180^\circ - \alpha-\beta-\beta = 180^\circ-\alpha-2\beta\),故選\(\bbox[red,2pt]{(D)}\)
解:
兩底面積和為16\(\Rightarrow\)上下底面積各為8\(\Rightarrow 8h=24\Rightarrow h=3\);
四個側面面積和為45\(\Rightarrow (a+b+c+d)h=45\Rightarrow a+b+c+d=45/3=15\),所有邊長和為\(2(a+b+c+d)+4h=2\times 15+4\times 3=30+12=42\),故選\(\bbox[red,2pt]{(C)}\)
解:
假設漱口水容量為A、瓶蓋容量為B,依題意\(A-\frac{B}{2}\times 10=\frac{3A}{4}\Rightarrow B=\frac{A}{20}\),剩下的漱口水還可以正確使用\(\frac{3A/4}{A/20/3}=45\)次,故選\(\bbox[red,2pt]{(B)}\)
解:
先算八位朋友的平均值, 八人體重與50的差距為 -4+-3+-1+0+2+3+5+6=8,因此8人體重的平均為 50+8/8=50+1=51;假設小傑體重為a,由於9人體重平均小於50,即\((51\times 8+a)/9 <50 \Rightarrow 408+a<450\Rightarrow a<42\),也就是說:小傑體重最輕;因此中位數就是排名第五的50公斤,全距>(56-42)=14,故選\(\bbox[red,2pt]{(A)}\)
解:
兩邊之和大於第三邊,所M在\(\overline{XY}\)上;又\(\overline{AX}>\overline{AY}\)及\(\overline{AY}+\overline{YM}=\overline{AX}+\overline{XM}\) 可推導出\(\overline{YM}>\overline{XM}\),也就是M離X較近,故選\(\bbox[red,2pt]{(C)}\)
解:
若a及b均為正值,其相對位置如上圖,只有選項(D)符合要求,故選\(\bbox[red,2pt]{(D)}\)
解:$$2009\times \left( -\frac { 2009 }{ 2008 } \right) =-2009\times \left( \frac { 2009 }{ 2008 } \right) =-2009\times \left( 1+\frac { 1 }{ 2008 } \right) =-\left( 2009+\frac { 2009 }{ 2008 } \right) \\ =-\left( 2009+1+\frac { 1 }{ 2008 } \right) =-\left( 2010+\frac { 1 }{ 2008 } \right) =-2010-\frac { 1 }{ 2008 } ,故選\bbox[red,2pt]{(C)}$$
解:$$\frac { 乙+丙 }{ 甲+乙+丙=全 } =\frac { (7+3)^{ 2 } }{ (7+3+2)^{ 2 } } =\frac { 100 }{ 144 } =\frac { 50 }{ 72 } \Rightarrow 乙+丙=\frac { 50 }{ 72 } 全\Rightarrow 甲=\frac { 22 }{ 72 } 全\\ \frac { 乙 }{ 乙+丙 } =\frac { 7^{ 2 } }{ (7+3)^{ 2 } } =\frac { 49 }{ 100 } \Rightarrow 乙=\frac { 49 }{ 100 } \left( 乙+丙 \right) =\frac { 49 }{ 100 } \times \frac { 50 }{ 72 } 全=\frac { 24.5 }{ 72 } 全\\ 乙=\frac { 49 }{ 100 } \left( 乙+丙 \right) \Rightarrow 丙=\frac { 51 }{ 100 } \left( 乙+丙 \right) =\frac { 51 }{ 100 } \times \frac { 50 }{ 72 } 全=\frac { 25.5 }{ 72 } 全\\ 由\begin{cases} 甲=\frac { 22 }{ 72 } 全 \\ 乙=\frac { 24.5 }{ 72 } 全 \\ 丙=\frac { 25.5 }{ 72 } 全 \end{cases}\Rightarrow 丙>乙>甲,故選\bbox[red,2pt]{(D)}$$
解:
由圖(二)可知:甲花了50秒追上乙,而且速度差是等速度,也就是9/50(公尺/秒),因此甲的速度是乙的速度加上速度差,即1.5+9/50,40秒之後,甲走了\((1.5+9/50)\times 40=60+36/5 = 60+7.2 =67.2\),故選\(\bbox[red,2pt]{(C)}\)
解:
\(\overline{BC}=20\Rightarrow \overline{BD}\div 2=10=\)圓半徑\(\Rightarrow \overline{BC}\)的中點就是切點,因此\(\overline{BC}\)的中垂線會經過圓心,故選\(\bbox[red,2pt]{(D)}\)。
解:
假設甲裝了a公升的水,乙裝了b公升的水
若甲水全倒入乙:乙內的水量為a+b,剩餘容量為 y-(a+b)=20;
若乙水倒入甲:乙倒了(b-10)給甲,即b-10+a=x;因此$$\begin{cases} y=20+a+b \\ x=a+b-10 \end{cases}\Rightarrow x-y=-30\Rightarrow y=x+30,故選\bbox[red,2pt]{(D)}$$
解:
假設每個正方形攤位的長度為\(a\),左、右兩側各有\(\frac{42-2a}{a}\)個攤位,上、下各有\(\frac{90-2a}{a}\)個攤位;以面積來算攤位數,即\(720\div a^2\),因此$$\frac { 42-2a }{ a } \times 2+\frac { 90-2a }{ a } \times 2=\frac { 720 }{ a^{ 2 } } \Rightarrow a(132-4a)=360\Rightarrow 4a^{ 2 }-132a+360=0\\ \Rightarrow a^{ 2 }-33a+90=0\Rightarrow (a-3)(a-30)=0\Rightarrow a=3(若a=30,則42-2a<0不合)\\ \Rightarrow 攤位數\frac { 720 }{ a^{ 2 } } =\frac { 720 }{ 9 } =80,故選\bbox[red,2pt]{(D)}$$
解:
1~207拿走數字除以3餘1的牌,也就是拿走1、4、7、10、...、202、205,即3n+1, n=0~68,共拿走69張牌,剩下207-69=138張牌;
剩下的牌為2、3、5、6、...、204、206、207,現在一次拿走最小與最的牌,即(2, 207)、(3,206)、(5,204)...也就是拿走兩數和為209的頭尾兩張牌;
只有選項(C)的兩數字和為209(104+105),故選\(\bbox[red,2pt]{(C)}\)
解:
\(Q\)是\(\overline{PB}\)的中點、\(O\)是\(\overline{AB}\)的中點,所以\(R\)是\(\triangle PAB\)的重心,因此\(\overline{OR}=\frac{1}{3}\overline{OP}\),由於\(\overline{OP}\)為半徑,長度不變,因此\(\overline{OR}\)長度也不變,故選\(\bbox[red,2pt]{(A)}\)
解:
假設牧場長為\(a\),寬為\(b\),如上圖,則圍籬的長度為\(3a+2b-2=82\Rightarrow 3a+2b=84\),牧場的面積為\(ab\);因此$$3a+2b=84\Rightarrow b=(84-3a)\div 2\Rightarrow ab=a\left( 84-3a \right) \div 2=\left( -3a^{ 2 }+84a \right) \div 2\\ =\left( -3\left( a^{ 2 }-28a+14^{ 2 } \right) +3\times 14^{ 2 } \right) \div 2=\left( -3{ \left( a-14 \right) }^{ 2 }+588 \right) \div 2\\ \Rightarrow 當a=14時,牧場面積ab有極大值588\div 2=\bbox[red,2pt]{294}$$
解:
各三角形面積標示如上圖,即\(\triangle ADF=a, \triangle FEM=b, \triangle DFM=c,\triangle CDM=e\);
\(\overline{AE}//\overline{DM}\Rightarrow \triangle ADM\)與\(\triangle DEM\)面積相同 (兩三角形同底,且高相等,所以面積一樣),即\(a+c=b+c \Rightarrow a=b \Rightarrow e+c+a=e+c+b \Rightarrow \triangle AMC=\triangle CDE\);
由於\(\overline{BM}=\overline{MC}\Rightarrow \triangle AMC=\frac{1}{2}\triangle ABC\),因此 \(\triangle CDE\)的面積也是\(\triangle ABC\)面積的一半。








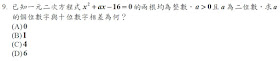























謝謝您,真是造福學子
回覆刪除教師節快樂
不客氣,希望大家可以不用補習.........
刪除