100 學年度國民中學運動成績優良學生
升學輔導甄試學科考試 數學科 試題
解:$$16\div 4\times(1+3)=16\div 4\times 4=4\times 4=16 ,故選\bbox[red,2pt]{(C)}$$
解:$$\sqrt{20}-5=\sqrt{5}a\Rightarrow a=\frac{\sqrt{20}-5}{\sqrt{5}}=\frac{(\sqrt{20}-5)\times \sqrt{5}}{\sqrt{5}\times\sqrt{5}}\\=\frac{10-5\sqrt{5}}{5}=2-\sqrt{5}\Rightarrow \begin{cases} m=2\\n=-1\end{cases}\Rightarrow m+n=2-1=1,故選\bbox[red,2pt]{(C)}$$
解:$$(1.2\times 10^{-7})\div(3\times 10^{-12}) = \frac{1.2\times 10^{-7}}{3\times 10^{-12}} =0.4\times 10^5 = 4\times 10^4,故選\bbox[red,2pt]{(A)}$$
解:$$假設第三邊長為a,若第三邊是斜邊,則a^2=(\sqrt{11})^2+5^2=36\Rightarrow a=6;\\若5是斜邊長,則5^2=(\sqrt{11})^2+a^2\Rightarrow a^2=14 \Rightarrow a=\sqrt{14};故選\bbox[red,2pt]{(D)}$$
解:$$\begin{cases} -\sqrt{24}=-2\sqrt{6}→不是 \\ \frac{\sqrt{27}}{11}=\frac{3\sqrt{3}}{11}→是\\\sqrt{18}=3\sqrt{2}→不是\\-\sqrt{120}=-4\sqrt{30}→不是\\\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}→是 \end{cases}\Rightarrow 有兩個和\sqrt{3}是同類方根,故選\bbox[red,2pt]{(B)}$$
解:$$\begin{cases} \frac{\sqrt{7}}{5}\\\frac{\sqrt{7}}{\sqrt{5}}=\frac{\sqrt{35}}{5} \\ \frac{7}{\sqrt{5}}=\frac{7\sqrt{5}}{5}\\\frac{7}{5} \end{cases}\Rightarrow 相同分母下取分子最大數,故選\bbox[red,2pt]{(C)}$$
解:$$\sqrt{(x-4)^2}+\sqrt{(y+3)^2}=0\Rightarrow \begin{cases}x-4=0\\y+3=0\end{cases} \Rightarrow \begin{cases}x=4\\y=-3\end{cases}\\\Rightarrow \sqrt{x+y}=\sqrt{1}=\pm 1,故選\bbox[red,2pt]{(C)}$$
解:$$1.5\times 10^{-7}\div 3\times 10^{-12}=\frac{1.5\times 10^{-7}}{3}\times 10^{-12} =0.5\times 10^{-7-12}=0.5\times 10^{-19}=5\times 10^{-20}\\,故選\bbox[red,2pt]{(D)}$$
解:$$\triangle ABC為直角三角形,非等腰三角形,因此\angle A之角平分線不會均分\overline{BC},故選\bbox[red,2pt]{(D)}$$
解:$$該路徑上所有的點至O點的距離皆相等,因此圖形為圓的一部份(弧),故選\bbox[red,2pt]{(A)}$$
解:
ABCDEFGH為正八邊形\(\Rightarrow \overline{AE}\)為直徑\(\Rightarrow \overline{AO} = \overline{OE}=\)半徑\(\Rightarrow \triangle AOD面積=\triangle ODC面積=\triangle ADE 面積\div 2 = 4\div 2 =2 \Rightarrow\) ABCDEFGH為正八邊形面積\(=\triangle ODC\times 8 = 2\times 8=16\),故選\(\bbox[red,2pt]{(A)}\)
解:$$假設第三邊長為a,若第三邊是斜邊,則a^2=(\sqrt{11})^2+5^2=36\Rightarrow a=6;\\若5是斜邊長,則5^2=(\sqrt{11})^2+a^2\Rightarrow a^2=14 \Rightarrow a=\sqrt{14};故選\bbox[red,2pt]{(D)}$$
解:$$\begin{cases} \frac{\sqrt{7}}{5}\\\frac{\sqrt{7}}{\sqrt{5}}=\frac{\sqrt{35}}{5} \\ \frac{7}{\sqrt{5}}=\frac{7\sqrt{5}}{5}\\\frac{7}{5} \end{cases}\Rightarrow 相同分母下取分子最大數,故選\bbox[red,2pt]{(C)}$$
解:$$\sqrt{(x-4)^2}+\sqrt{(y+3)^2}=0\Rightarrow \begin{cases}x-4=0\\y+3=0\end{cases} \Rightarrow \begin{cases}x=4\\y=-3\end{cases}\\\Rightarrow \sqrt{x+y}=\sqrt{1}=\pm 1,故選\bbox[red,2pt]{(C)}$$
解:$$1.5\times 10^{-7}\div 3\times 10^{-12}=\frac{1.5\times 10^{-7}}{3}\times 10^{-12} =0.5\times 10^{-7-12}=0.5\times 10^{-19}=5\times 10^{-20}\\,故選\bbox[red,2pt]{(D)}$$
解:$$\triangle ABC為直角三角形,非等腰三角形,因此\angle A之角平分線不會均分\overline{BC},故選\bbox[red,2pt]{(D)}$$
解:$$該路徑上所有的點至O點的距離皆相等,因此圖形為圓的一部份(弧),故選\bbox[red,2pt]{(A)}$$
解:
解:$$ x^2+2x-9408=0 \Rightarrow (x^2+2x+1)-9408-1=0 \Rightarrow (x+1)^2-9409=0 \\\Rightarrow x+1=97 \Rightarrow x=96,故選\bbox[red,2pt]{(A)}$$
解:$$\overline{AB}: \overline{BC}: \overline{CA} =\sqrt{3}:\sqrt{5}:\sqrt{7} \Rightarrow \overline{CA}>\overline{BC}>\overline{AB} \Rightarrow \angle B>\angle A>\angle C,故選\bbox[red,2pt]{(B)}$$
解:
解:
上圖之\(\triangle DBA\)與\(\triangle CBA\)符合SSA條件,但兩三角形並不全等,故選\(\bbox[red,2pt]{(C)}\)
解:
若圖形按實際比例應為上圖,若\(\overline{BP}\bot\overline{AC}\),則P點落在線段 \(\overline{AC}\)之外。因此若要符合P點在AC之間移動,則P=A時 \(\overline{AP} +\overline{BP} +\overline{CP}= \overline{AC}+\overline{AB}=5+5=10\)為最小值,故選\(\bbox[red,2pt]{(D)}\)
此題題目恐有疑義,在其他考試\(\overline{BC}=6\),P點就會落在A、C之間,則答案就是9.8,選項\(\bbox[red,2pt]{(C)}\)就是答案。
解:
作\(\overline{GH}\bot\overline{AB}\),見上圖。令圓半徑為\(r=\overline{AD}=\overline{AG}\),則\(\overline{GH}=\overline{FB}=r/2\);
因此在直角\(\triangle AGH\)中,\(\overline{GH}:\overline{AG}=1:2 \Rightarrow \angle AGH=60^\circ \Rightarrow \angle AGF=60^\circ + 90^\circ = 150^\circ\),故選\(\bbox[red,2pt]{(D)}\)
解:$$\angle A=90^\circ 且I為內心 \Rightarrow \angle IAB=45^\circ \Rightarrow 直線\overline{AI}的斜率為1\\斜率為1且經過(3/2,1)的直線方程式為 y-1=x-3/2 \Rightarrow 當x=0時,y-1=-3/2\\ \Rightarrow y=-1/2,故選\bbox[red,2pt]{(A)}$$
解:
$$ y=\frac{1}{3}x+2 \Rightarrow y-2=\frac{1}{3}x\Rightarrow x=3y-6\Rightarrow 小蓉蓉年齡是兒子的3倍少6歲\\,故選\bbox[red,2pt]{(D)}$$
解:
直線L經過\((0,b)及(b/100,0)\),見上圖,故選\(\bbox[red,2pt]{(A)}\)
解:$$\begin{cases} S_{ 10 }=100 \\ S_{ 20 }=50 \end{cases}\Rightarrow \begin{cases} \frac { \left( 2a_{ 1 }+9d \right) \times 10 }{ 2 } =100 \\ \frac { \left( 2a_{ 1 }+19d \right) \times 20 }{ 2 } =50 \end{cases}\Rightarrow \begin{cases} 2a_{ 1 }+9d=20 \\ 2a_{ 1 }+19d=5 \end{cases}\Rightarrow 10d=-15\Rightarrow d=-1.5\\ \Rightarrow 2a_{ 1 }-13.5=20\Rightarrow a_{ 1 }=16.75\Rightarrow S_{ 30 }=\frac { \left( 2a_{ 1 }+29d \right) \times 30 }{ 2 } =\left( 33.5-43.5 \right) \times 15=-150\\,故選\bbox[red,2pt]{(D)}$$
解:
解:$$ 2(2x-1)-x=7x \Rightarrow 4x-2-x=7x\Rightarrow -2=4x \Rightarrow x=-\frac{1}{2} ,故選\bbox[red,2pt]{(A)}$$
解:$$ax+by=1通過(0,1/b)及(1/a, 0),不通過第二象限\Rightarrow 1/a>0且1/b<0\\ \Rightarrow b<0, a>0 \Rightarrow (b,a )在第二象限,故選\bbox[red,2pt]{(B)}$$
解:$$\begin{cases}(A)a\div b\div c=\frac{a}{b}\div c=\frac{a}{bc}\\(B)a\times\frac{1}{c} \div b = \frac{a}{cb}\\(C)a\div\frac{1}{c\times b}=a\times c\times b\\ (D) a\div (c\times b)=\frac{a}{c\times b}\end{cases},故選\bbox[red,2pt]{(C)}$$
解:$$101\times\frac{101}{100}=\frac{(100+1)^2}{100}=\frac{100^2+2\times 100+1}{100}=100+2+\frac{1}{100}=102+\frac{1}{100},故選\bbox[red,2pt]{(C)}$$
解:$$\begin{cases} S_{ 35 }=158 \\ S_{ 12 }=66 \end{cases}\Rightarrow \begin{cases} \frac { \left( 2a_{ 1 }+34d \right) \times 35 }{ 2 } =158 \\ \frac { \left( 2a_{ 1 }+11d \right) \times 12 }{ 2 } =66 \end{cases}\Rightarrow \begin{cases} 2a_{ 1 }+34d=\frac { 316 }{ 35 } \\ 2a_{ 1 }+11d=11 \end{cases}\Rightarrow 23d=-\frac { 69 }{ 35 } \Rightarrow d=-\frac { 3 }{ 35 } \\ \Rightarrow 2a_{ 1 }-11\times \frac { 3 }{ 35 } =11\Rightarrow a_{ 1 }=\frac { 209 }{ 35 } \Rightarrow a_{ 24 }=a_{ 1 }+23d=\frac { 209 }{ 35 } -\frac { 3 }{ 35 } \times 23=\frac { 140 }{ 35 } =4\\,故選\bbox[red,2pt]{(A)}$$
解:$$f(0)+f(9)-f(4)=6+(-5)-7=-6,故選\bbox[red,2pt]{(A)}$$
解:$$(3x^2+5x+4)-(3x^2-5x+2)=10x+2,故選\bbox[red,2pt]{(C)}$$
解:
假設濃度為6%的食鹽水有\(x\)公克,則鹽占\(0.06x\)公克,白開水占\(0.94x\)公克;
加了白開水70公克後,濃度變為5%,即\(\frac{0.06x}{70+0.94x}=\frac{5}{100} \Rightarrow 70+0.94x=1.2x\);
再加70公克的白開水,濃度變為a%,即\(\frac{0.06x}{70+70+0.94x}=\frac{a}{100}\Rightarrow a=\frac{6x}{70+1.2x}=5-\frac{350}{70+1.2x}\);
由於\(0<\frac{350}{70+1.2x}<1\Rightarrow 4<a<5\),故選\(\bbox[red,2pt]{(D)}\)
解:$$\frac{3}{5}a=b+\frac{2}{5}a\Rightarrow \frac{1}{5}a=b\Rightarrow \frac{a}{b}=5,故選\bbox[red,2pt]{(D)}$$
解:
\(16+17\times 2=60\Rightarrow \)確定當選;
若有3個人的票都比小参多,則總票數至少是\(17\times 3+16=67\)超過總投票數60,故選\(\bbox[red,2pt]{(A)}\)
解:
解:$$\sqrt { \frac { a^{ 2 }+b^{ 2 } }{ 4 } +\frac { ab }{ 2 } } =\sqrt { { \left( \frac { a }{ 2 } \right) }^{ 2 }+2\cdot \frac { a }{ 2 } \cdot \frac { b }{ 2 } +{ \left( \frac { b }{ 2 } \right) }^{ 2 } } =\sqrt { { \left( \frac { a }{ 2 } +\frac { b }{ 2 } \right) }^{ 2 } } =\sqrt { { \left( \frac { a+b }{ 2 } \right) }^{ 2 } } \\ =\frac { a+b }{ 2 } =\frac { 19+13 }{ 2 } =\frac { 32 }{ 2 } =16,故選\bbox[red,2pt]{(C)}$$
解:
解:14與15互質,但都不是質數,故選\(\bbox[red,2pt]{(D)}\)
解:
$$令O_1半徑r_1,O_2半徑r_2=2, O_3半徑r_3=3,\\ 在\overline{DO_3}上找一點P,使得\overline{CP} // \overline{O_2O_3};並在\overline{CO_2}上找一點Q,使得\overline{BQ} // \overline{O_1O_2},見上圖\\ \triangle BCQ\sim \triangle CDP(AAA) \Rightarrow \frac{\overline{BQ}}{\overline{CQ}}=\frac{\overline{CD}}{\overline{DP}} \Rightarrow \frac{r_1+r_2}{r_2-r_1}=\frac{r_2+r_3}{r_3-r_2}\Rightarrow \frac{2+r_1}{2-r_1}=\frac{5}{1} \\ r_1=\frac{8}{6}=\frac{4}{3}\Rightarrow O_1直徑=2r_1=\bbox[red,2pt]{\frac{8}{3}}$$
解:
在四邊形中,\(\angle A+\angle B+\angle C=360^\circ-\angle 1\);同理\(\angle D+\angle E+\angle F=360^\circ-\angle 2\)及\(\angle G+\angle H+\angle I=360^\circ-\angle 3\);
因此\(\angle A+\angle B+\cdots+\angle I=360\times 3-(\angle 1+\angle 2+\angle 3)\) = \(1080^\circ -(\angle 1+\angle 2+\angle 3)\);
又\(\angle 1=\angle 4 \Rightarrow \angle A+\angle B+\cdots+\angle I=1080^\circ -(\angle 4+\angle 2+\angle 3)=1080^\circ-180^\circ = 900^\circ\),故選\(\bbox[red,2pt]{(C)} \)
解:
解:
--END--
解:$$\overline{AB}: \overline{BC}: \overline{CA} =\sqrt{3}:\sqrt{5}:\sqrt{7} \Rightarrow \overline{CA}>\overline{BC}>\overline{AB} \Rightarrow \angle B>\angle A>\angle C,故選\bbox[red,2pt]{(B)}$$
解:
內角加外角為180度,外角不可能是360度,故選\(\bbox[red,2pt]{(A)}\)
上圖之\(\triangle DBA\)與\(\triangle CBA\)符合SSA條件,但兩三角形並不全等,故選\(\bbox[red,2pt]{(C)}\)
此題題目恐有疑義,在其他考試\(\overline{BC}=6\),P點就會落在A、C之間,則答案就是9.8,選項\(\bbox[red,2pt]{(C)}\)就是答案。
解:
作\(\overline{GH}\bot\overline{AB}\),見上圖。令圓半徑為\(r=\overline{AD}=\overline{AG}\),則\(\overline{GH}=\overline{FB}=r/2\);
因此在直角\(\triangle AGH\)中,\(\overline{GH}:\overline{AG}=1:2 \Rightarrow \angle AGH=60^\circ \Rightarrow \angle AGF=60^\circ + 90^\circ = 150^\circ\),故選\(\bbox[red,2pt]{(D)}\)
解:$$\angle A=90^\circ 且I為內心 \Rightarrow \angle IAB=45^\circ \Rightarrow 直線\overline{AI}的斜率為1\\斜率為1且經過(3/2,1)的直線方程式為 y-1=x-3/2 \Rightarrow 當x=0時,y-1=-3/2\\ \Rightarrow y=-1/2,故選\bbox[red,2pt]{(A)}$$
解:
$$ y=\frac{1}{3}x+2 \Rightarrow y-2=\frac{1}{3}x\Rightarrow x=3y-6\Rightarrow 小蓉蓉年齡是兒子的3倍少6歲\\,故選\bbox[red,2pt]{(D)}$$
解:
直線L經過\((0,b)及(b/100,0)\),見上圖,故選\(\bbox[red,2pt]{(A)}\)
解:$$\begin{cases} S_{ 10 }=100 \\ S_{ 20 }=50 \end{cases}\Rightarrow \begin{cases} \frac { \left( 2a_{ 1 }+9d \right) \times 10 }{ 2 } =100 \\ \frac { \left( 2a_{ 1 }+19d \right) \times 20 }{ 2 } =50 \end{cases}\Rightarrow \begin{cases} 2a_{ 1 }+9d=20 \\ 2a_{ 1 }+19d=5 \end{cases}\Rightarrow 10d=-15\Rightarrow d=-1.5\\ \Rightarrow 2a_{ 1 }-13.5=20\Rightarrow a_{ 1 }=16.75\Rightarrow S_{ 30 }=\frac { \left( 2a_{ 1 }+29d \right) \times 30 }{ 2 } =\left( 33.5-43.5 \right) \times 15=-150\\,故選\bbox[red,2pt]{(D)}$$
解:
直走5步再向右轉45度,相當於在畫一個正n多邊形;45度的外角為180-45=135度,由$$\frac{(n-2)\times 180}{n}=135 \Rightarrow n=8$$因此機器人畫了一個正八邊形,故選\(\bbox[red,2pt]{(B)}\)
解:$$ 2(2x-1)-x=7x \Rightarrow 4x-2-x=7x\Rightarrow -2=4x \Rightarrow x=-\frac{1}{2} ,故選\bbox[red,2pt]{(A)}$$
解:$$ax+by=1通過(0,1/b)及(1/a, 0),不通過第二象限\Rightarrow 1/a>0且1/b<0\\ \Rightarrow b<0, a>0 \Rightarrow (b,a )在第二象限,故選\bbox[red,2pt]{(B)}$$
解:$$\begin{cases}(A)a\div b\div c=\frac{a}{b}\div c=\frac{a}{bc}\\(B)a\times\frac{1}{c} \div b = \frac{a}{cb}\\(C)a\div\frac{1}{c\times b}=a\times c\times b\\ (D) a\div (c\times b)=\frac{a}{c\times b}\end{cases},故選\bbox[red,2pt]{(C)}$$
解:$$101\times\frac{101}{100}=\frac{(100+1)^2}{100}=\frac{100^2+2\times 100+1}{100}=100+2+\frac{1}{100}=102+\frac{1}{100},故選\bbox[red,2pt]{(C)}$$
解:$$\begin{cases} S_{ 35 }=158 \\ S_{ 12 }=66 \end{cases}\Rightarrow \begin{cases} \frac { \left( 2a_{ 1 }+34d \right) \times 35 }{ 2 } =158 \\ \frac { \left( 2a_{ 1 }+11d \right) \times 12 }{ 2 } =66 \end{cases}\Rightarrow \begin{cases} 2a_{ 1 }+34d=\frac { 316 }{ 35 } \\ 2a_{ 1 }+11d=11 \end{cases}\Rightarrow 23d=-\frac { 69 }{ 35 } \Rightarrow d=-\frac { 3 }{ 35 } \\ \Rightarrow 2a_{ 1 }-11\times \frac { 3 }{ 35 } =11\Rightarrow a_{ 1 }=\frac { 209 }{ 35 } \Rightarrow a_{ 24 }=a_{ 1 }+23d=\frac { 209 }{ 35 } -\frac { 3 }{ 35 } \times 23=\frac { 140 }{ 35 } =4\\,故選\bbox[red,2pt]{(A)}$$
解:$$f(0)+f(9)-f(4)=6+(-5)-7=-6,故選\bbox[red,2pt]{(A)}$$
解:$$(3x^2+5x+4)-(3x^2-5x+2)=10x+2,故選\bbox[red,2pt]{(C)}$$
解:
加了白開水70公克後,濃度變為5%,即\(\frac{0.06x}{70+0.94x}=\frac{5}{100} \Rightarrow 70+0.94x=1.2x\);
再加70公克的白開水,濃度變為a%,即\(\frac{0.06x}{70+70+0.94x}=\frac{a}{100}\Rightarrow a=\frac{6x}{70+1.2x}=5-\frac{350}{70+1.2x}\);
解:$$\frac{3}{5}a=b+\frac{2}{5}a\Rightarrow \frac{1}{5}a=b\Rightarrow \frac{a}{b}=5,故選\bbox[red,2pt]{(D)}$$
若有3個人的票都比小参多,則總票數至少是\(17\times 3+16=67\)超過總投票數60,故選\(\bbox[red,2pt]{(A)}\)
解:
內角和定理:三角形三內角和為180度,故選\(\bbox[red,2pt]{(D)}\)
解:$$\sqrt { \frac { a^{ 2 }+b^{ 2 } }{ 4 } +\frac { ab }{ 2 } } =\sqrt { { \left( \frac { a }{ 2 } \right) }^{ 2 }+2\cdot \frac { a }{ 2 } \cdot \frac { b }{ 2 } +{ \left( \frac { b }{ 2 } \right) }^{ 2 } } =\sqrt { { \left( \frac { a }{ 2 } +\frac { b }{ 2 } \right) }^{ 2 } } =\sqrt { { \left( \frac { a+b }{ 2 } \right) }^{ 2 } } \\ =\frac { a+b }{ 2 } =\frac { 19+13 }{ 2 } =\frac { 32 }{ 2 } =16,故選\bbox[red,2pt]{(C)}$$
解:
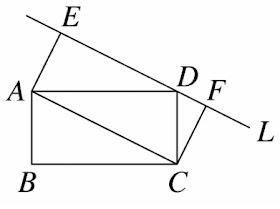
作\(\overline{DG}//\overline{FC}\),見上圖;$$\triangle CDF面積=\triangle DGC面積 且\triangle ADE面積=\triangle面積 ADG \\ \Rightarrow \triangle ADE+\triangle CDF=\triangle ADC=\triangle ABC \Rightarrow a=b\Rightarrow a:b=1:1,故選\bbox[red,2pt]{(D)}$$
解:14與15互質,但都不是質數,故選\(\bbox[red,2pt]{(D)}\)
解:
\(\bbox[red,2pt]{(無正確選項)}\)
解:
在四邊形中,\(\angle A+\angle B+\angle C=360^\circ-\angle 1\);同理\(\angle D+\angle E+\angle F=360^\circ-\angle 2\)及\(\angle G+\angle H+\angle I=360^\circ-\angle 3\);
因此\(\angle A+\angle B+\cdots+\angle I=360\times 3-(\angle 1+\angle 2+\angle 3)\) = \(1080^\circ -(\angle 1+\angle 2+\angle 3)\);
又\(\angle 1=\angle 4 \Rightarrow \angle A+\angle B+\cdots+\angle I=1080^\circ -(\angle 4+\angle 2+\angle 3)=1080^\circ-180^\circ = 900^\circ\),故選\(\bbox[red,2pt]{(C)} \)
解:
鈍角三角形的外心不在三角形內,故選\(\bbox[red,2pt]{(B)}\)
解:
0沒有倒數,故選\(\bbox[red,2pt]{(B)}\)
--END--





























沒有留言:
張貼留言