桃連區桃園市立內壢高級中等學校
108學年度高級中等學校特色招生考試
數學科詳解
解:
$$\sqrt { 12 } \times \left( \frac { 1 }{ \sqrt { 2 } } -\frac { 1 }{ \sqrt { 3 } } \right) =\sqrt { 12 } \times \left( \frac { \sqrt { 3 } -\sqrt { 2 } }{ \sqrt { 6 } } \right) =\sqrt { 2 } \times \left( \sqrt { 3 } -\sqrt { 2 } \right) \\ =\sqrt { 6 } -2,故選\bbox[red,2pt]{(A)}。$$
解:$$a=8051=90^{ 2 }-7^{ 2 }=\left( 90+7 \right) \left( 90-7 \right) =97\times 83(97,83皆為質數)\\ \left( A \right) 7不是因數\\ \left( B \right) 37不是因數\\ \left( C \right) 質因數只有兩個83及97\\ \left( D \right) 正因數的和=1+83+97+8051=8232\\,故選\bbox[red,2pt]{(D)}。$$
解:
由題意可知B坐標為(-4,4),因此直線AB的方程式為\(y=x/4+5\),故選\(\bbox[red,2pt]{(A)}\)。
解:
$$\begin{cases} 2020x+2019y=2021\cdots (1) \\ 2019x+2020y=2018\cdots (2) \end{cases}\xrightarrow { (1)+(2),(1)-(2) } \begin{cases} 4039x+4039y=4039 \\ x-y=3 \end{cases}\Rightarrow \begin{cases} x+y=1 \\ x-y=3 \end{cases}\\ \Rightarrow \begin{cases} x=a=2 \\ y=b=-1 \end{cases}\Rightarrow a+2b=2-2=0,故選\bbox[red,2pt]{(C)}。$$
解:
扇形AED面積=八分之一圓=\(4^2\pi\times\frac{1}{8}=2\pi\);
扇形FEG面積=四分之一圓=\(2^2\pi\times\frac{1}{4}=\pi\);
三角形FGA面積=\(2\times 2\div 2=2\);
封閉區域DGE=扇形AED-扇形FEG-三角形FGA=\(2\pi-\pi-2=\pi-2\),故選\(\bbox[red,2pt]{(D)}\)。
解:
$$x^{ 2 }-670x-2019=0\Rightarrow \left( x-673 \right) \left( x+3 \right) =0\Rightarrow a=673,b=-3,故選\bbox[red,2pt]{(B)}。$$
解:$$E在x+y=1上\Rightarrow p+q=1\Rightarrow \begin{cases} x=\frac{p}{p^2-q^2}=\frac{p}{(p+q)(p-q)} =\frac{p}{p-q} \\ y=\frac{q}{p^2-q^2}=\frac{q}{(p+q)(p-q)}=\frac{q}{p-q} \end{cases}\\\Rightarrow \frac{p}{p-q}-\frac{q}{p-q}=1\Rightarrow x-y=1,故選\bbox[red,2pt]{(D)}。$$
解:$$2x^{ 2 }+ax-2=(cx-1)(-2x+b)+2=-2cx^{ 2 }+(bc+2)x-b+2\\ \Rightarrow \begin{cases} -2c=2 \\ bc+2=a \\ -b+2=-2 \end{cases}\Rightarrow \begin{cases} c=-1 \\ a=-2 \\ b=4 \end{cases}\Rightarrow 2a+b+c=-4+4-1=-1,故選\bbox[red,2pt]{(B)}。$$
解:
解:$$(A)\times :若k=0,圖形經過(1,0)\\ (B)\times :y=x^{ 2 }-2x+1+k,開口向上\\ (C)\bigcirc :\begin{cases} a={ \left( 1-2019 \right) }^{ 2 }+k=2018^{ 2 }+k \\ b={ \left( 1-2020 \right) }^{ 2 }+k=2019^{ 2 }+k \end{cases}\Rightarrow b-a=2019^{ 2 }-2018^{ 2 }>0\\ (D)\times :開口向上有最低點\\,故選\bbox[red,2pt]{(C)}。$$
解:$$\begin{cases} 2a=3b \\ a:c=2:3 \end{cases}\Rightarrow \begin{cases} b=\frac { 2 }{ 3 } a \\ c=\frac { 3 }{ 2 } a \end{cases}\Rightarrow \frac { 4c-a }{ a+b } =\frac { 6a-a }{ a+\frac { 2 }{ 3 } a } =\frac { 5a }{ \frac { 5 }{ 3 } a } =3,故選\bbox[red,2pt]{(B)}。$$
解:
延長直線\(\overline{DC}\)與直線\(\overline{FB}\)相交於Q點,如上圖;$$\overline{AD}//\overline{BD}\Rightarrow \triangle QDF\sim\triangle QPB\Rightarrow \frac{\overline{QD}}{\overline{QC}} = \frac{\overline{FD}}{\overline{BC}}\Rightarrow \frac{\overline{QD}}{\overline{QD}+12m} = \frac{n}{\overline{4n}}\Rightarrow \overline{QD}=4m\\ \overline{DC}//\overline{AB}\Rightarrow \frac{\overline{CP}}{\overline{PE}} = \frac{\overline{QC}}{\overline{EB}} =\frac{4m+12m}{7m}=\frac{16}{7}=\frac{\triangle DPC}{\triangle DEP},故選\bbox[red,2pt]{(A)}$$
解:
(甲)\(\times: \)若公差\(d=-0.1\Rightarrow a_{10}=a_1+9d=1-0.9=0.1>0\),但\(a_{100}=a_1+99d=1-9.9<0\)
(乙)\(\bigcirc:a_{10}<0\Rightarrow a_1+9d<0\Rightarrow d<0\Rightarrow a_{100} = a_1+99d= a_1+9d+90d=a_{10}+90d<0\)
(丙)\(\bigcirc: a_{100}-a_{10}=a_1+99d-a_1-9d=90d=10\times 9d=10(a_1+9d-a_1)=10(a_{10}-a_1)\)
故選\(\bbox[red,2pt]{(B)}\)。
解:
解:
解:
(A), (B), (D) 皆對稱紅線,故選\(\bbox[red,2pt]{(C)}\)。
解:
$$y=x^2-6x+(9+\sqrt{3})=(x-3)^2+\sqrt{3}\Rightarrow 頂點P=(3,\sqrt{3}) \Rightarrow \begin{cases} \overline{PQ}=\sqrt{3} \\ \overline{BQ}=3 \\ \overline{PB}=2\sqrt{3} \end{cases} \\\Rightarrow \angle PBA=30^\circ \Rightarrow \angle ABC=60^\circ \\ 同理\angle CAB=60^\circ \Rightarrow \triangle ABC為正三角形\Rightarrow \triangle ABC面積=6\times 3\sqrt{3}\div 2 =9\sqrt{3},故選\bbox[red,2pt]{(A)}。$$
解:
\overline{OE}=\overline{OC}(都是正方形邊長)\Rightarrow \overline{OE}=\overline{OC}=\overline{OB}=\overline{OA}=r \\ \Rightarrow O是\triangle AEB的外接圓圓心也就是外心\\也是\triangle EBC的外接圓圓心也就是外心, 故選\bbox[red,2pt]{(C)}。$$
解:
解:
解:$$\frac{n}{n+4+6}=\frac{1}{3}\Rightarrow n+10=3n \Rightarrow n=5,故選\bbox[red,2pt]{(D)}。$$
解:
$$90分鐘=\frac{90}{60}=\frac{3}{2}小時,假設甲地至乙地花了t小時,則乙至丙花了\frac{3}{2}-t 小時\\ \Rightarrow 84t+96(\frac{3}{2}-t)=134 \Rightarrow 42t+72-48t=67 \Rightarrow t=\frac{5}{6}小時=\frac{5}{6}\times 60=50分鐘,故選\bbox[red,2pt]{(D)}。$$
解:
解:
$$平圴數為4\Rightarrow (4+8+1+5+6+m+n)\div 7=4 \Rightarrow m+n=4\\ \Rightarrow \begin{array}{c|c|c|c|c}m&n&a&b&c \\\hline1&3&1&4&7\\\hline 2&2&2&4&7\\\hline3&1&1&4&7\end{array},故選\bbox[red,2pt]{(C)}$$
解:
(甲)\angle ABC=3a=3\times 45=135^\circ\\(乙) \angle AEB=\angle BED=180-45-45=90^\circ \Rightarrow \begin{cases}\overline{AE} =\overline{EP}=1\\ \overline{EB}=\overline{EB}\\\angle AEB=\angle EDB=90^\circ \end{cases} \Rightarrow 符合SAS全等條件\\ (丙)面積=\overline{AD}\times\overline{EB} = 2\times 1=2\ne\sqrt{3},故選\bbox[red,2pt]{(B)}$$
解:
作\(\overline{DE}\bot\overline{BC}\),如上圖。
由於\(\overline{CD}\)為\(\angle C\)的角平分線,所以\(\triangle CAD\cong \triangle CED \Rightarrow\) \(\overline{CA}=\overline{CE}=3\)且\(\overline{AD}=\overline{DE}=3/2\);
又\(\angle BED=\angle A=90^\circ\)且\(\angle B=\angle B\),所以\(\triangle BED\sim\triangle BAC\),因此$$\frac{\overline{ED}}{\overline{AC}}=\frac{\overline{DB}}{\overline{BC}} =\frac{\overline{EB}}{\overline{AB}} \Rightarrow \frac{3/2}{3}=\frac{b}{3+a}= \frac{a}{b+3/2} \\ \Rightarrow \begin{cases}3b=9/2+3a/2\\3a=9/4+3b/2\end{cases} \Rightarrow \begin{cases}a-2b+3=0\\ 4a-2b-3=0\end{cases}\Rightarrow \begin{cases} a=2\\b=5/2\end{cases} \Rightarrow \overline{AB}=3/2+5/2=4$$,故選\(\bbox[red,2pt]{(D)}\)。
解:
四捨五入後成為(0,0,1,1,1,1,2),(0+2,0+2,1+2,1+2,1+2,1+2,2+2)\dots\\
每7個一組,計算其總和,成為6,6+2\times 7,6+4\times 7,\dots\\
a_1至a_{32},每7個一組,可分成4組再加上a_{29},a_{30},a_{31},a_{32},\\
因此a_1+\cdots+a_{28}=(7a_1+6)+(7a_1+6+2\times 7)+(7a_1+6+4\times 7)+(7a_1+6+6\times 7)\\=28a_1+108=164\\
又a_{29}+a_{30}+a_{31}+a_{32}=4a_1+8+8+9+9=8+34=42\\
a_1+\cdots+a_{32}=164+42=206,故選\bbox[red,2pt]{(B)}。$$
解:
$$假設長方體邊長分別為r,s,t,則\begin{cases}rst=a\\rs=12\\2(rs+st+rt)=108\end{cases}\Rightarrow \begin{cases}t=a/12\\rs=12\\t(r+s)=42\end{cases} \\\Rightarrow \begin{cases}t=a/12\\rs=12\\a=42\times 12/(r+s)\end{cases} \Rightarrow
\begin{array}{c|c|c|c}r&s&r+s&a\\\hline 1&12&13&非整數\\\hline 6&2&8&63\\\hline 4&3&7&72\\\hline3&4&7&72\\\hline 2&6&8&63\\\hline1&12&13&非整數\end{array},故選\bbox[red,2pt]{(A)}。$$
解:
邊長為2的正方形有\(4\times 3=12\)個;
邊長為3的正方形有\(3\times 2=6\)個;
邊長為4的正方形有\(2\times 1=2\)個;
正方形總共有\(20+12+6+2=40\)個,故選\(\bbox[red,2pt]{(A)}\)。
解:
每個9點畫一條直線,在畫第n條線後回到A點,也就是找最小的n,使得9n是48的倍數,即$$\frac{48n}{9}=\frac{3n}{16}\Rightarrow n=16,故選\bbox[red,2pt]{(C)}。$$
解:
作\(\overline{MQ}//\overline{AP}\)及\(\overline{RN}//\overline{SA}\),並假設正方形邊長為\(a\),如上圖;
由於\(\overline{MQ}//\overline{AP}\Rightarrow \angle SQM=\angle P\)且\(\angle SMQ=\angle RNP=90^\circ\),所以$$\triangle SMQ\sim\triangle RNP \Rightarrow \frac{\overline{MQ}}{\overline{NP}}=\frac{\overline{SQ}}{\overline{RP}} \Rightarrow \frac{a}{\overline{NP}} =\frac{3/5}{5/4} \Rightarrow \overline{NP}=\frac{3}{4}a\\ 在直角\triangle RNP中, {\overline{RP}}^2 ={\overline{RN}}^2+{\overline{NP}}^2\\ (5/4)^2=a^2+(3a/4)^2 \Rightarrow 25/16=25a^2/16 \Rightarrow a=1(a=-1不合)$$
解:
由於\(\overline{MQ}//\overline{AP}\Rightarrow \angle SQM=\angle P\)且\(\angle SMQ=\angle RNP=90^\circ\),所以$$\triangle SMQ\sim\triangle RNP \Rightarrow \frac{\overline{MQ}}{\overline{NP}}=\frac{\overline{SQ}}{\overline{RP}} \Rightarrow \frac{a}{\overline{NP}} =\frac{3/5}{5/4} \Rightarrow \overline{NP}=\frac{3}{4}a\\ 在直角\triangle RNP中, {\overline{RP}}^2 ={\overline{RN}}^2+{\overline{NP}}^2\\ (5/4)^2=a^2+(3a/4)^2 \Rightarrow 25/16=25a^2/16 \Rightarrow a=1(a=-1不合)$$
答:正方形的邊長為\(\bbox[red,2pt]{1}\)
解:
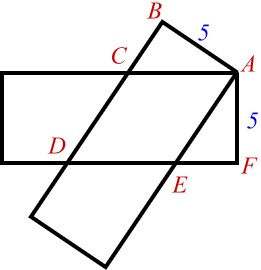
將其中一張紙片上下及左右平移,使得紙片的右上角重疊,如上圖;
由於兩紙片皆為長方形,所以\(\overline{AC}//\overline{DE}\)且\(\overline{AE}//\overline{CD}\),因此紙片重疊區域為一平行四邊形;
觀察三角形AFE與三角形ABC,\(\angle FAE+\angle EAC=90^\circ=\angle BAC+\angle EAC \Rightarrow \angle FAE=\angle CAB\),又\(\angle F=\angle B=90^\circ\)及\(\overline{AF}=\overline{AB}=5\),兩三角形符合AAS,即兩三角形全等;
由於兩三角形全等,所以\(\overline{AC}=\overline{AE}\),因此兩紙片重疊區域不僅是平行四邊形,更是菱形,其面積為\(5\overline{AC}\);
由題意知:重疊區域面積=兩長方形面積扣掉多邊形面積=\(12\times 5\times 2-94=26=5\overline{AC} \Rightarrow \overline{AC}=\frac{26}{5}\);
多邊形周長=兩長方形周長扣掉菱形周長=\((12+5)\times 4 - 4\times \frac{26}{5}=\frac{236}{5}\);
答:周長為\(\bbox[red,2pt]{\frac{236}{5}}\)
- END -














































請問108年桃連區內壢高中特招數學第七題, 解答算式第一行, p+q為何等於1??
回覆刪除謝謝
因為E(p,q)在X加Y等於1上,p=x;q=y
刪除