高雄區公立高中 106 學年度聯合招考轉學生
升高二數學科試題詳解
升高二數學科試題詳解
一、單選題
$$\log_7 \left( 48^3+3\cdot 48^2+3\cdot 48+1 \right) =\log_7 (48+1)^3 =3\log_7 49=6, 故選:\bbox[red,2pt]{(E)}$$
解:
$${1 \over 5^2} +{1\over 4^2} +1={16+25+25\times 16 \over 25\times 16} ={441 \over 400} ={21^2 \over 20^2} \Rightarrow \sqrt{{1 \over 5^2} +{1\over 4^2} +1}= \sqrt{21^2 \over 20^2}\\ ={21\over 20}= 1.05,故選\bbox[red,2pt]{(B)}$$
解:
$$\begin{cases}ab>0 \\ ac<0 \end{cases} \Rightarrow \begin{cases}斜率-a/b < 0\\ X截距-c/a> 0\end{cases} \Rightarrow 不通過第三象限, 故選\bbox[red,2pt]{(C)}$$
解:$$\begin{cases}1人贏: C^4_1\times 3=12\\ 2人贏: C^4_2\times 3=18 \\3人贏: C^4_3\times 3=12\end{cases} \Rightarrow 分出勝負的情況有12+18+12=42種\\ \Rightarrow 不分勝負=全部-分出勝負= 3^4-42=81-42=39 , 故選\bbox[red,2pt]{(B)}$$
解:
$$\begin{array}{}
a & b &\\\hline
1 & 6\\ 2& 5 \\ 3& 4 &\\4 & 3 & V\\ 5 & 2\\ 6& 1\\\hline
\end{array}\\ a+b=7的事件有6種,其中b=3只有一種,因此機率為1/6, 故選\bbox[red,2pt]{(A)}$$
解:
$$先考慮(x-1)^7(x-3)^3(x-9)^4=0 \Rightarrow x=1,3,4\\
再考慮(x-1)^7(x-3)^3(x-9)^4<0,由於(x-9)^4\ge 0,只要考慮(x-1)^7(x-3)^3<0\\ \Rightarrow 1<x<3 \Rightarrow x=2;因此所有的整數解為1,2,3,4,共四個, 故選\bbox[red,2pt]{(D)}$$
解:$$(x+ay)^7= \sum_{i=0}^7C^7_ix^i(ay)^{7-i} \Rightarrow x^4y^3的係數為C^7_4a^{3} =-280 \Rightarrow a^3= -{280 \over C^7_4} =-{280 \over 35}=-8\\ \Rightarrow a=-2,故選\bbox[red,2pt]{(A)} $$
解:
$$\begin{cases}a = 2.6^{10}-2.6^9 = (2.6-1)\times 2.6^9 =1.6\times 2.6^9 \\ b =2.6^{11}- 2.6^{10} = (2.6-1)\times 2.6^{10} =1.6\times 2.6^{10} \\ c=(2.6^{11}-2.6^9)/2 = (2.6^2-1)\times 2.6^9 /2 =2.88 \times 2.6^9\end{cases} \Rightarrow b>c>a,故選\bbox[red,2pt]{(D)} $$
解:$$\begin{cases}a = \log_{1/5}3 = -\log 3/\log 5\\ b =\log_{1/3} 5 =-\log 5/\log 3\\ c= \log_{1/3}{1\over 5} = \log 5/\log 3 \\ d= \log_{1/5}{1\over 3} = \log 3/\log 5\end{cases} \Rightarrow c>d>a>b,故選\bbox[red,2pt]{(D)}$$
解:
$$ x^2-2x-3>0 \Rightarrow (x-3)(x+1) >0 \Rightarrow A=\{x\mid x>3 或x<-1,x \in R\}\\ 由 \begin{cases} A\cup B=R \Rightarrow \{x\mid -1\le x \le 3 \} \in B\\A\cap B=\{x\mid 3<x\le 4, x\in R\}\end{cases} \Rightarrow B=\{x \mid -1\le x\le 4\}\\ \Rightarrow (x-4)(x+1)\le 0 \Rightarrow x^2-3x-4\le 0 \Rightarrow \begin{cases}b = -3\\ c=-4 \end{cases} \Rightarrow b+c=-7,故選\bbox[red,2pt]{(E)}$$
解:$$\begin{cases}EX = (1+2+\cdots +n)/n =(n+1)/2 \\EX^2 = (1^2+2^2+ \cdots +n^2)/n = (n+1)(2n+1)/6\end{cases} \Rightarrow Var(X)=EX^2 -(EX)^2\\ \Rightarrow (\sqrt {10})^2 = {(n+1)(2n+1) \over 6} -{(n+1)^2 \over 4} \Rightarrow 10= {2n^2+3n+1 \over 6} -{ n^2+2n+1 \over 4} \\ \Rightarrow 120= 4n^2+6n+2-3n^2-6n-3 = n^2-1 \Rightarrow n^2 = 121 \Rightarrow n=11,故選\bbox[red,2pt]{(C)}$$
解:
$$三名觀眾A、B、C,在兩人中間插空位,形成x_1Ax_2Bx_3Cx_4,其中x_1+x_2+x_3+x_4=6(個空位)\\依題意要求,x_2及x_3需大於0,x_1\dots x_4均小於3,因此有以下情況:\\ \begin{array}{c|c|cc|cc|ccc} x_1 & 2& 1 & 2 & 1 & 2& 1& 0 & 2\\\hline x_2 &1 &2 & 2 & 1 & 1& 2 & 2 & 2 \\\hline x_3 & 1 & 1& 1& 2 & 2 & 2& 2 & 2 \\\hline x_4 & 2 & 2& 1& 2& 1& 1 & 2& 0\end{array}\\ 總共有8種(x_1,x_2,x_3,x_4)符合要求,每一種的ABC有3!排法,共有8\times 3!;全部有8\times 7\times 6\\因此機率為{8\times 3! \over 8\times 7\times 6} ={2\over 21},故選\bbox[red,2pt]{(C)}$$
解:
$$\begin{array}{}
a_{200} & =& a_{199}+(3\times 199+1)\\
a_{199} & =& a_{198}+(3\times 198+1)\\
a_{198} & =& a_{197}+(3\times 197+1)\\
\dots & &\dots\\
a_2 & = & a_1+(3\times 1+1)
\end{array}\\上式全部相加 \Rightarrow a_{200}= a_1+ 3(1+2+\cdots+199)+199 =200 + 3\times 200\times 199 \div 2 = 59900\\,故選\bbox[red,2pt]{(E)}$$
解:$$(A) \times: \begin{cases} a=i \\ b=1 \end{cases} \Rightarrow a^2+b^2 =-1+1=0,但a\ne 0且b\ne 0\\(B) \times: \begin{cases}\begin{cases}a=i \\b=-i \end{cases} \Rightarrow a+bi= 1+i\\\begin{cases}c=1 \\ d=1 \end{cases} \Rightarrow c+di= 1+i\end{cases} \Rightarrow a+bi=c+di, 但a\ne c且b\ne d\\ 其它皆正確\\,故選\bbox[red,2pt]{(CDE)}$$
解:
$$此題由兩圖形的交點數目可得\\(A) \times: y=x與y=2^x無交點\\(C)\times: y=x^2與y=2^x有3個交點\\(D)\times: y=2^x與x+2有兩個交點\\其餘皆一個;交點\\,故選\bbox[red,2pt]{(BE)} $$
解:$$(C) \times : 3個人是不同的,應該是3!\times C^9_5C^4_2C^2_2\\(D) \times: 理由同(C)\\(E)\times: 理由同(C) \\,故選\bbox[red,2pt]{(AB)}$$
解:$$令f(x)=3x^3-11x^2+25x-25 \Rightarrow \begin{cases} f(1)=3-11+25-25<0 \\ f(2)= 24-44+50-25>0 \end{cases} \Rightarrow 1,2間有實根\\ 假設a為其實根,則f(x)=(x-a)(3x^2+bx+c) = 3x^3+(b-3a)x^2+(c-ab)x-ac \\ \Rightarrow \begin{cases} b-3a=-11\\ c-ab = 25 \\ ac=25\end{cases} \Rightarrow \begin{cases} b=3a-11\\ c=ab + 25 = a(3a-11)+25 = 3a^2-11a+25 \end{cases}\\ 3x^2+bx+c 的判別式 \triangle =b^2-12c =(3a-11)^2-12( 3a^2-11a+25) =-27a^2+66a-179 <0 \\\Rightarrow 3x^2+bx+c=0 有兩虛根 \Rightarrow f(x)=0 有一實根兩虛根,故選\bbox[red, 2pt]{(ACDE)}$$
解:$$g(x)= x^3+3x^2+4x+2 =(x^2+ax+b)(x+(3-a))+3x+2\\ \Rightarrow g(0)=2= b(3-a)+2 \Rightarrow b(3-a)=0 \Rightarrow a=3或b=0\\ 同理h(x) =x^3+x^2-x-1=(x^2+ax+b)(x+(1-a))+4x+1\\ \Rightarrow h(0)=-1=b(1-a)+1 \Rightarrow b(1-a)=-2\cdots(1)\\
b=0代入(1) \Rightarrow 無解;a=3代入(1) \Rightarrow -2b=-2 \Rightarrow b=1\\ (A)\bigcirc: a=3\\(B)\times: b=1\\(C)\times: f(x)=0 \Rightarrow x^2+3x+1=0 \Rightarrow 判別式9-4>0 有實根\\(D)\times: f(x)=x^2+3x+1=(x+3/2)^2-5/4 \Rightarrow 最小值為-5/4\\(E) \bigcirc: f(-3)=9-9+1=1 \Rightarrow 餘式為1\\,故選\bbox[red, 2pt]{(AE)}$$
解:$$(A)\bigcirc: 9^n的個位數= \begin{cases} 1 & n是偶數\\ 9 & n是奇數 \end{cases} \Rightarrow 9^{70}的個位數字為1\\(B) \bigcirc: \log 9^{70}=70\log 9=140\log 3=140\times 0.4771 =66.794 \Rightarrow 9^{70}是67位數\\(C) \times: \log 9^{70}的小數部分為0.794 \Rightarrow \log 6= 0.7781 <0.794 < 0.8451= \log 7\Rightarrow 最左數字是6\\(D)\times: \log {1\over x}=-\log x = -66.794 =-67 +(1-0.794) =-67+0.206 \\\qquad \Rightarrow 小數點後第67位不為零\\(E) \times:\log 1=0< 0.206 <0.301=\log 2 \Rightarrow 不為0的數字是1\\,故選\bbox[red, 2pt]{(AB)}$$
解:$$(A)\bigcirc: \fbox{$\phantom{3}$}可填0-9,有10種選擇,機率為1/10\\(B) \times: 同(A)有10種選擇,伹需最簡分數,\fbox{$\phantom{3}$}不可填0,3,6,9,機率為1/6\\(C) \bigcirc: \begin{array}{c|c|c|c|c|c|c|c|c|c} a&1,3,5,7,9&1,2,3,5,7,8&1,3,5,7,9& 1-4,6-9 & 1,5,7&1-6,8,9 & 1,3,5,7,9 & 1,2,3,4,7,8\\\hline b& 2 & 3& 4& 5& 6& 7& 8 & 9\end{array} \\\qquad \Rightarrow {a\over b}共有5+6+5+8+3+8+5+6 =46種\Rightarrow 機率為1/46\\(D)\times: \begin{array}{cc|c} \fbox{$\phantom{3}$} & \fbox{$\phantom{3}$} &數量\\\hline - & 1-9 &9\\ \pm & 1-9 &9\\ 1& 0-9 &10\\ 2& 0-9 &10\\ \dots\\ 9& 0-9 &10\\ \hline &合計 &108 \end{array} \Rightarrow 機率為1/108\\(E) \bigcirc:坐標(\fbox{$\phantom{3}$},\fbox{$\phantom{3}$}), 每個\fbox{$\phantom{3}$}可填0-9,共100種,機率為1/100\\,故選\bbox[red, 2pt]{(ACE)}$$
解題僅供參考
$${1 \over 5^2} +{1\over 4^2} +1={16+25+25\times 16 \over 25\times 16} ={441 \over 400} ={21^2 \over 20^2} \Rightarrow \sqrt{{1 \over 5^2} +{1\over 4^2} +1}= \sqrt{21^2 \over 20^2}\\ ={21\over 20}= 1.05,故選\bbox[red,2pt]{(B)}$$
$$\begin{cases}ab>0 \\ ac<0 \end{cases} \Rightarrow \begin{cases}斜率-a/b < 0\\ X截距-c/a> 0\end{cases} \Rightarrow 不通過第三象限, 故選\bbox[red,2pt]{(C)}$$
解:$$\begin{cases}1人贏: C^4_1\times 3=12\\ 2人贏: C^4_2\times 3=18 \\3人贏: C^4_3\times 3=12\end{cases} \Rightarrow 分出勝負的情況有12+18+12=42種\\ \Rightarrow 不分勝負=全部-分出勝負= 3^4-42=81-42=39 , 故選\bbox[red,2pt]{(B)}$$
$$\begin{array}{}
a & b &\\\hline
1 & 6\\ 2& 5 \\ 3& 4 &\\4 & 3 & V\\ 5 & 2\\ 6& 1\\\hline
\end{array}\\ a+b=7的事件有6種,其中b=3只有一種,因此機率為1/6, 故選\bbox[red,2pt]{(A)}$$
解:
$$令迴歸直線L: y=ax+b,由題意知該直線通過(65,70)及(5,46)\\ \Rightarrow \begin{cases}65a +b=70 \cdots(1) \\ 5a+b=46 \cdots(2)\end{cases} \Rightarrow (1)-(2) \Rightarrow 60a=24 \Rightarrow a=0.4, 故選\bbox[red,2pt]{(A)}$$解:
$$先考慮(x-1)^7(x-3)^3(x-9)^4=0 \Rightarrow x=1,3,4\\
再考慮(x-1)^7(x-3)^3(x-9)^4<0,由於(x-9)^4\ge 0,只要考慮(x-1)^7(x-3)^3<0\\ \Rightarrow 1<x<3 \Rightarrow x=2;因此所有的整數解為1,2,3,4,共四個, 故選\bbox[red,2pt]{(D)}$$
解:$$(x+ay)^7= \sum_{i=0}^7C^7_ix^i(ay)^{7-i} \Rightarrow x^4y^3的係數為C^7_4a^{3} =-280 \Rightarrow a^3= -{280 \over C^7_4} =-{280 \over 35}=-8\\ \Rightarrow a=-2,故選\bbox[red,2pt]{(A)} $$
解:
$$\begin{cases}a = 2.6^{10}-2.6^9 = (2.6-1)\times 2.6^9 =1.6\times 2.6^9 \\ b =2.6^{11}- 2.6^{10} = (2.6-1)\times 2.6^{10} =1.6\times 2.6^{10} \\ c=(2.6^{11}-2.6^9)/2 = (2.6^2-1)\times 2.6^9 /2 =2.88 \times 2.6^9\end{cases} \Rightarrow b>c>a,故選\bbox[red,2pt]{(D)} $$
解:$$\begin{cases}a = \log_{1/5}3 = -\log 3/\log 5\\ b =\log_{1/3} 5 =-\log 5/\log 3\\ c= \log_{1/3}{1\over 5} = \log 5/\log 3 \\ d= \log_{1/5}{1\over 3} = \log 3/\log 5\end{cases} \Rightarrow c>d>a>b,故選\bbox[red,2pt]{(D)}$$
解:
$$ x^2-2x-3>0 \Rightarrow (x-3)(x+1) >0 \Rightarrow A=\{x\mid x>3 或x<-1,x \in R\}\\ 由 \begin{cases} A\cup B=R \Rightarrow \{x\mid -1\le x \le 3 \} \in B\\A\cap B=\{x\mid 3<x\le 4, x\in R\}\end{cases} \Rightarrow B=\{x \mid -1\le x\le 4\}\\ \Rightarrow (x-4)(x+1)\le 0 \Rightarrow x^2-3x-4\le 0 \Rightarrow \begin{cases}b = -3\\ c=-4 \end{cases} \Rightarrow b+c=-7,故選\bbox[red,2pt]{(E)}$$
解:
$$\sum_{k=1}^{99}k(k+1) = \sum_{k=1}^{99}(k^2+k) = \sum_{k=1}^{99}k^2 +\sum_{k=1}^{99} k ={1\over 6}99(99+1)(2\times 99+1) +{1\over 2}(99+1)99\\ = 99\times 100 ({1\over 6}\times 199+{1\over 2}) = 99\times 100 ({199+3\over 6}) = 99\times 100\times {101 \over 3},故選\bbox[red,2pt]{(B)}$$
解:
$$\begin{array}{}
a_{200} & =& a_{199}+(3\times 199+1)\\
a_{199} & =& a_{198}+(3\times 198+1)\\
a_{198} & =& a_{197}+(3\times 197+1)\\
\dots & &\dots\\
a_2 & = & a_1+(3\times 1+1)
\end{array}\\上式全部相加 \Rightarrow a_{200}= a_1+ 3(1+2+\cdots+199)+199 =200 + 3\times 200\times 199 \div 2 = 59900\\,故選\bbox[red,2pt]{(E)}$$
二、多重選擇題
解:$$(A)\times: -1>-2,但(-1)^2 < (-2)^2 \\(B) \times: -1>-2且 -2>-3,但(-1)\times (-2) <(-2) \times (-3)\\(E) \times: 若x=0,y=1 \Rightarrow x^2+y^2=1 <5 \\ 其它皆正確\\,故選\bbox[red,2pt]{(CD)}$$
解:
$$此題由兩圖形的交點數目可得\\(A) \times: y=x與y=2^x無交點\\(C)\times: y=x^2與y=2^x有3個交點\\(D)\times: y=2^x與x+2有兩個交點\\其餘皆一個;交點\\,故選\bbox[red,2pt]{(BE)} $$
解:$$(C) \times : 3個人是不同的,應該是3!\times C^9_5C^4_2C^2_2\\(D) \times: 理由同(C)\\(E)\times: 理由同(C) \\,故選\bbox[red,2pt]{(AB)}$$
解:$$令f(x)=3x^3-11x^2+25x-25 \Rightarrow \begin{cases} f(1)=3-11+25-25<0 \\ f(2)= 24-44+50-25>0 \end{cases} \Rightarrow 1,2間有實根\\ 假設a為其實根,則f(x)=(x-a)(3x^2+bx+c) = 3x^3+(b-3a)x^2+(c-ab)x-ac \\ \Rightarrow \begin{cases} b-3a=-11\\ c-ab = 25 \\ ac=25\end{cases} \Rightarrow \begin{cases} b=3a-11\\ c=ab + 25 = a(3a-11)+25 = 3a^2-11a+25 \end{cases}\\ 3x^2+bx+c 的判別式 \triangle =b^2-12c =(3a-11)^2-12( 3a^2-11a+25) =-27a^2+66a-179 <0 \\\Rightarrow 3x^2+bx+c=0 有兩虛根 \Rightarrow f(x)=0 有一實根兩虛根,故選\bbox[red, 2pt]{(ACDE)}$$
解:$$g(x)= x^3+3x^2+4x+2 =(x^2+ax+b)(x+(3-a))+3x+2\\ \Rightarrow g(0)=2= b(3-a)+2 \Rightarrow b(3-a)=0 \Rightarrow a=3或b=0\\ 同理h(x) =x^3+x^2-x-1=(x^2+ax+b)(x+(1-a))+4x+1\\ \Rightarrow h(0)=-1=b(1-a)+1 \Rightarrow b(1-a)=-2\cdots(1)\\
b=0代入(1) \Rightarrow 無解;a=3代入(1) \Rightarrow -2b=-2 \Rightarrow b=1\\ (A)\bigcirc: a=3\\(B)\times: b=1\\(C)\times: f(x)=0 \Rightarrow x^2+3x+1=0 \Rightarrow 判別式9-4>0 有實根\\(D)\times: f(x)=x^2+3x+1=(x+3/2)^2-5/4 \Rightarrow 最小值為-5/4\\(E) \bigcirc: f(-3)=9-9+1=1 \Rightarrow 餘式為1\\,故選\bbox[red, 2pt]{(AE)}$$
解:$$(A)\bigcirc: 9^n的個位數= \begin{cases} 1 & n是偶數\\ 9 & n是奇數 \end{cases} \Rightarrow 9^{70}的個位數字為1\\(B) \bigcirc: \log 9^{70}=70\log 9=140\log 3=140\times 0.4771 =66.794 \Rightarrow 9^{70}是67位數\\(C) \times: \log 9^{70}的小數部分為0.794 \Rightarrow \log 6= 0.7781 <0.794 < 0.8451= \log 7\Rightarrow 最左數字是6\\(D)\times: \log {1\over x}=-\log x = -66.794 =-67 +(1-0.794) =-67+0.206 \\\qquad \Rightarrow 小數點後第67位不為零\\(E) \times:\log 1=0< 0.206 <0.301=\log 2 \Rightarrow 不為0的數字是1\\,故選\bbox[red, 2pt]{(AB)}$$
解:$$(A)\bigcirc: \fbox{$\phantom{3}$}可填0-9,有10種選擇,機率為1/10\\(B) \times: 同(A)有10種選擇,伹需最簡分數,\fbox{$\phantom{3}$}不可填0,3,6,9,機率為1/6\\(C) \bigcirc: \begin{array}{c|c|c|c|c|c|c|c|c|c} a&1,3,5,7,9&1,2,3,5,7,8&1,3,5,7,9& 1-4,6-9 & 1,5,7&1-6,8,9 & 1,3,5,7,9 & 1,2,3,4,7,8\\\hline b& 2 & 3& 4& 5& 6& 7& 8 & 9\end{array} \\\qquad \Rightarrow {a\over b}共有5+6+5+8+3+8+5+6 =46種\Rightarrow 機率為1/46\\(D)\times: \begin{array}{cc|c} \fbox{$\phantom{3}$} & \fbox{$\phantom{3}$} &數量\\\hline - & 1-9 &9\\ \pm & 1-9 &9\\ 1& 0-9 &10\\ 2& 0-9 &10\\ \dots\\ 9& 0-9 &10\\ \hline &合計 &108 \end{array} \Rightarrow 機率為1/108\\(E) \bigcirc:坐標(\fbox{$\phantom{3}$},\fbox{$\phantom{3}$}), 每個\fbox{$\phantom{3}$}可填0-9,共100種,機率為1/100\\,故選\bbox[red, 2pt]{(ACE)}$$
解題僅供參考




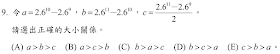












沒有留言:
張貼留言