110年大學學測-數學詳解

110 學年度學科能力測驗試題

一、單選題

解：$$A=\begin{bmatrix} 1 & 2 \\ 0 & 3\end{bmatrix} \Rightarrow A^2=\begin{bmatrix} 1 & 8 \\ 0 & 9\end{bmatrix} \Rightarrow A^4=A^2A^2= \begin{bmatrix} 1 & 80 \\ 0 & 81\end{bmatrix} =\begin{bmatrix} a & b \\ c & d\end{bmatrix} \\\Rightarrow  a+b+c+d =1+80+ 0+81 =162，故選\bbox[red,2pt]{(2)}$$

解：$$a_1=\log 36 = 2\log 6 \Rightarrow \cases{a_2=2a_1 = 4\log 6\\ a_2={1\over 2}a_1= \log 6 < 1(不合)} \Rightarrow a_2= 4\log 6 \Rightarrow \cases{a_3=2a_2=8\log 6\\ a_3={1\over 2}a_2 = 2\log 6} \\\Rightarrow \cases{a_4=2a_3 = 16\log 6,4\log 6\\ a_4={1\over 2}a_3 = 4\log 6(\log 6 < 1,不合)} \Rightarrow \cases{a_5=2a_4=32\log 6,8\log 6 \\ a_5={1\over 2}a_4=8\log 6,2\log 6} \\ \Rightarrow a_5=2\log 6,8\log 6, 32\log 6，有三種可能的值，故選\bbox[red,2pt]{(1)}$$

解：

$$假設O為圓心，則\angle OCP=\angle OBP=90^\circ \Rightarrow \angle BOC = 180^\circ-\theta \Rightarrow \angle A={1\over 2}\angle BOC = 90^\circ-{1\over 2}\theta \\ \Rightarrow \cos A=\cos(90^\circ-{1\over 2}\theta) =\sin{1\over 2}\theta，故選\bbox[red,2pt]{(3)}$$

解：$$\cases{\vec a=(m,n)\\ \vec b=(s,t)} \Rightarrow \cases{2\vec a+\vec b=(2m+s,2n+t)\\ \vec a+2\vec b=(m+2s,n+2t)\\ 3\vec a+\vec b=(3m+s,3n+t)\\ \vec a+3\vec b=(m+3s,n+3t)} \Rightarrow由題意知 {1\over 2}\begin{Vmatrix}2m+s & 2n+t\\ m+2s & n+2t\end{Vmatrix} =6 \\ \Rightarrow |mt-ns|=4，再計算{1\over 2}\begin{Vmatrix}3m+s & 3n+t\\ m+3s & n+3t\end{Vmatrix} = 4|mt-ns|= 4\times 4=16，故選\bbox[red,2pt]{(5)}$$

解：$$(x+1)f(x)=(x^3+2)(ax+b)+x+2 \Rightarrow \cases{(-1+1)f(-1)=(-1+2)(-a+b)-1+2\\ (0+1)f(0)=(0+2)(0+b)+0+2} \\ \Rightarrow \cases{a-b=1 \\ 4=2b+2} \Rightarrow \cases{a=2\\ b=1} \Rightarrow (x+1)f(x)= (x^3+2)(2x+1) +x+2\\ \Rightarrow (2+1)f(2)=10\cdot 5+4 \Rightarrow f(2)=18，故選\bbox[red,2pt]{(4)}$$

 

解：

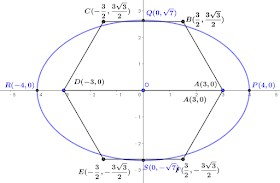
$$\cases{A(3,0)\\ D(-3,0)} \Rightarrow \cases{B({3\over 2},{3\sqrt 3\over 2}) \\C(-{3\over 2},{3\sqrt 3\over 2}) \\ E(-{3\over 2},-{3\sqrt 3\over 2}) \\F({3\over 2},-{3\sqrt 3\over 2}) };又 {x^2\over 4^2} +{y^2\over (\sqrt 7)^2} =1 \Rightarrow 橢圓四頂點\cases{P(4,0)\\ Q(0,\sqrt 7) \\ R(-4,0)\\ S(0,-\sqrt 7)}\\ 由於\cases{u=\text{dist}(O,\overline{BC})= {3\sqrt 3\over 2} \Rightarrow u^2={27\over 4} =6.75 < (\sqrt 7)^2 \\ \overline{OP} > \overline{OA}}\\ 因此兩圖形有8個交點，故選\bbox[red,2pt]{(5)}$$

二、多選題

解：$$(1)\times: 有0.4的機率被看成8\\ (2)\bigcirc: 1-0.4=0.6\\(3)\bigcirc: \cases{6被誤看的機率:1-0.4=0.6\\ 8被誤看的機率:1-0.4=0.6\\ 9被誤看的機率:1-0.5=0.5} \Rightarrow 9被誤看的機率最低\\(4)\bigcirc: {0.4\over 0.4+0.3+0.2}={4\over 9} < 0.5\\(5)\times: {0.5\over 0.2+0.1+0.5}={5\over 8}=0.625 < {2\over 3}(=0.67)\\故選\bbox[red,2pt]{(2,3,4)}$$

解：

$$(1) \times:A(3,4)\Rightarrow \cases{\overline{OA}= \sqrt{3^2+4^2} =5 \\ L斜率m={4\over 3}} \Rightarrow \cases{\Gamma:x^2+y^2=25\\ L:3y=4x} \Rightarrow L與\Gamma 另一交點為(-3,-4)\\(2)\times: \overrightarrow{OA} =\overrightarrow{BC} \Rightarrow L\parallel \overleftrightarrow{BC} \Rightarrow \overline{BC}斜率=m=4/3 \\(3)\bigcirc: B(a,b) \Rightarrow C(a+3,b+4) \Rightarrow \overline{AC}=\sqrt{a^2+b^2}=5 \Rightarrow \triangle AOC為正\triangle \Rightarrow  \angle AOC=60^\circ \\(4)\times: \overline{OA}=\overline{OB} =\overline{AC}=\overline{BC}=5 \Rightarrow OACB 為一菱形 \Rightarrow \triangle CBA面積={1\over 2}\cdot\overline{CA}\cdot \overline{CB}\cdot\sin \angle ACB \\ \qquad= {1\over 2}\cdot 5\cdot 5\cdot \sin 120^\circ ={25\over 4}\sqrt 3\\(5)  \bigcirc:A逆時鐘旋轉60^\circ即為C、旋轉120^\circ即為B \Rightarrow \cases{C=\begin{bmatrix}\cos 60^\circ & -\sin 60^\circ\\ \sin 60^\circ & \cos 60^\circ\end{bmatrix} \begin{bmatrix} 3 \\ 4\end{bmatrix} = \begin{bmatrix} 負值 \\ 正值\end{bmatrix}\\ B= \begin{bmatrix}\cos 120^\circ & -\sin 120^\circ\\ \sin 120^\circ & \cos 120^\circ\end{bmatrix} \begin{bmatrix} 3 \\ 4\end{bmatrix} = \begin{bmatrix} 負值 \\ 正值\end{bmatrix}}\\ \qquad\Rightarrow B、C均在第二象限；同理，A順時鐘旋轉60^\circ 即為C、旋轉120^\circ即為B，兩點均在第四象限；\\故選\bbox[red,2pt]{(3,5)}$$

解：$$\begin{array}{|c|r|r|}\hline  & 甲 & 乙\\\hline 第1投票所& 0.4x & 0.6x \\\hline 第2投票所 & 0.55y & 0.45y\\\hline\end{array}\\(1)\times:知道x+y，無法判定0.4x+0.55y與0.6x+0.45y的大小\\(2)\bigcirc: {x\over y}=k \Rightarrow \cases{甲: 0.4x+0.55y=0.4ky+0.55y = (0.4k+0.55)y\\ 乙: 0.6x+0.45y=0.6ky+0.45y= (0.6k+0.45)y} \xrightarrow{k=0.5}\cases{甲:0.75y\\乙: 0.75y} \\ \qquad \Rightarrow \begin{cases} 甲\gt 乙& k < 1/2\\ 甲=乙& k=1/2\\乙\gt 甲 & k > 1/2 \end{cases}\\(3) \bigcirc: x > y \Rightarrow {x\over y} > 1 >{1\over 2}\Rightarrow 乙\gt 甲 \\(4)\bigcirc:0.4 x> 0.55y \Rightarrow {x\over y} > {55\over 40} >{1\over 2} \Rightarrow 乙當選\\(5)\times: 0.45y > 0.6x \Rightarrow {x\over y} < {45\over 60}=0.75 \Rightarrow \cases{x/y < 0.5 \Rightarrow 甲勝\\ 1/2 < x/y < 0.75 \Rightarrow 乙勝}\\故選\bbox[red,2pt]{(2,3,4)}$$

解：

$$假設\overline{BC}=a > 0\\ (1)\bigcirc: k=\cos A ={4^2+6^2-a^2 \over 2\cdot 4\cdot 6} \Rightarrow a^2=52-48k \Rightarrow a=\sqrt{52-48k},可求得唯一a值\\(2)\bigcirc: 理由同(1)\\(3)\times: 見上圖，\triangle ABC與\triangle AB'C有相同的\angle C，及邊長4與6，但\overline{BC}\ne \overline{B'C}，無法決定唯一的\overline{BC}\\(4) \times:已知\triangle ABC = {1\over 2}\cdot 4\cdot 6\cdot \sin A \Rightarrow \sin A為已知 \Rightarrow \angle A也可能是(180^\circ-\angle A)，2種可能\\(5)\times: {a\over \sin A} = 2R \Rightarrow \sin A為已知 ，理由同(4)，\angle A可能有2種可能\\ 故選\bbox[red,2pt]{(1,2)}$$

解：

$$在\overline{CD}上找一點E，使得\overline{AE}= \overline{BC}，則ABCE為一平行四邊形，見上圖；\\(1)\bigcirc:\triangle ADE中，\overline{AD}\gt \overline{AE} \Rightarrow \angle AED \gt \angle D (大角對大邊) \Rightarrow \angle AED+\angle DAE \gt \angle D+\angle DAE \\ \qquad \Rightarrow   \angle BAE+\angle DAE \gt  \angle AEC \Rightarrow \angle A > \angle B \\(2) \bigcirc:\angle B+\angle D= \angle AEC+\angle D=180^\circ-\angle AED +\angle D < 180^\circ (\because \angle AED > \angle D) \\(3)\times:\angle B不一定是鈍角\\(4)\times: k=2 \Rightarrow \triangle ADE三邊長分別為2,3,5，不符合2邊和大於第3邊\\(5) \bigcirc:\cos \angle C = \cos \angle AED ={25+k^2-(k+1)^2 \over 10k} ={12-k\over 5k}   \Rightarrow \overrightarrow{CB} \cdot \overrightarrow{CD}= 15k\cos \angle C\\\qquad =15k\times {12-k\over 5k} =36-3k \\ \qquad若36-3k < 30 則k \gt 2；由於(k+1)+k > 5 \Rightarrow k > 2符合要求。\\故選\bbox[red,2pt]{(125)}$$

解：$$7顆球任排: {7!\over 2!2! 3!} =210\\A:\{黑球相鄰 \} \Rightarrow \#(A)={6!\over 2!3!}=60  \\ C:\{任2紅球不相鄰\} \Rightarrow \#(C)=全部-有2紅球相鄰+3紅球相鄰=210-{6!\over 2!2!} +{5!\over 2!2!} \\\qquad =210-180+30=60\\A\cap C:\{黑球相鄰且任2紅球不相鄰\} \Rightarrow \#(A\cap C)= {6!\over 2!3!}-{5!\over 2!}+{4!\over 2!}=60-60+12=12\\ B\cap C:\{黑球不相鄰且任2紅球不相鄰\}=\#(C)-\#(A\cap C)=60-12=48\\(1)\times: \cases{ P(A)=60/210\\ P(B)=1-P(A)=150/210 }\Rightarrow P(B)\gt P(A)\\(2)\bigcirc:P(C)=60/210=2/7\\(3)\times: 2P(C|A)+5P(C|B) = 2{P(A\cap C)\over P(A)} +5{P(B\cap C)\over P(B)} =2{12\over 60}+5{48\over 150}=2 \not \lt 2\\(4)\times: P(C|A)={P(A\cap C)\over P(A)}={12\over 60}={1\over 5}=0.2 \not \gt 0.2\\(5)\bigcirc: P(C|B)= {P(B\cap C)\over P(B)}={48\over 150}={32\over 100}=0.32 \gt 0.3\\ 故選\bbox[red,2pt]{(2,5)}$$

解：$$(1)\times: x^3+ax^2+bx+c = x^2+100 \Rightarrow x^3+(a-1)x^2+bx+c-100=0，三次式一定有實數解，即一定有交點\\(2)\bigcirc: f(0)f(1) \lt 0 \lt f(0)f(2) \Rightarrow f(0)f(1)f(0)f(2) < 0 \Rightarrow \cases{f(0)f(1) \lt 0 \\f^2(0)f(1)f(2) < 0 \Rightarrow f(1)f(2) < 0} \\ \qquad \Rightarrow \cases{有1根介於0與1之間\\ 有1根介於1與2之間},又f(x)為3次式，因此有3相異實根 \\(3)\bigcirc: x=1+3i \Rightarrow x^2-2x+10=0 \Rightarrow f(x)=(x^2-2x+10)(x-k)，由於f(x)係數皆為有理數，因此k為有理數\\ (4)\times: \cases{f(1)=a+b+c+1\\ f(2)=4a+2b+c+8 \\f(3)=9a+3b+ c+27\\ f(4)=16a+4b+c+64} \Rightarrow \cases{f(2)-f(1)=3a+b+7 \cdots(1)\\ f(3)-f(2)=5a+b+19\cdots(2) \\ f(4)-f(3)=7a+b+37 \cdots(3)} \\ \qquad \Rightarrow \cases{(1)=(2) \Rightarrow 2a+12=0 \Rightarrow a=-6\\ (2)=(3) \Rightarrow 2a+18=0 \Rightarrow a=-9} 矛盾\\(5)\bigcirc: {f(2)\over f(1)} ={f(3)\over f(2)} ={f(4)\over f(3)}=r \Rightarrow \cases{f(2)=rf(1) \\ f(3)=rf(2) \\ f(4)=rf(3)} \Rightarrow \cases{ (4-r)a +(2-r)b+(1-r)c=r-8 \\ (9-4r)a+(3-2r)b+(1-r)c=8r-27 \\ (16-9r)a+(4-3r)b+(1-r)c =27r-64} \\ \qquad 可利用克拉瑪公式可求得a,b,c，由於各係數皆為有理數，其行列式亦為有理數\\\qquad 例:取r=2 \Rightarrow f(x)=x^3-3x^2+8x \Rightarrow \cases{f(1)=6\\ f(2)=12\\ f(3)=24\\ f(4)=48} \Rightarrow f(1),f(2),f(3),f(4)為等比數列\\故選\bbox[red,2pt]{(2,3,5)}$$

第貳部份、選填題

解：每週期移動\(4\times 6=24\)單位，由於\(116=24\times 4+20\)；也就是歷經4週期(\(8\times 4=32\)秒)再加\(20\div 4=5\)秒，即\(32+5=\bbox[red,2pt]{37}\)秒。

解：$$\cases{L_1:(2s,-3s,-5s)\\ L_2:(1,1+2t,1+3t)} \Rightarrow \cases{L_1的方向向量\vec u=(2,-3,-5)\\ L_2的方向向量\vec v=(0,2,3)}  \Rightarrow E的法向量\vec n= \vec u\times \vec v=(1,-6,4)\\ E過L_1上的P(0,0,0) \Rightarrow  \bbox[red,2pt]{x-6y+4z=0}$$

解：$$\cases{4^2=16=1\times 2\times 8\\ 6^2=36=1\times 4\times 9 =2\times 3\times 6\\8^2= 64=2\times 4\times 8\\ 12^2=144=2\times 8\times 9 =3\times 6\times 8} ，共6組，機率為{6\over C^{9}_3} ={6\over 84} =\bbox[red,2pt]{1\over 14}$$

解：

解：$$\cases{y=a\cdot 2^{x}經過(-1,3) \Rightarrow 3= a\cdot 2^{-1} \Rightarrow a=6\\ y=a\cdot 2^{x}經過(-1,-1) \Rightarrow -1= a\cdot 2^{-1} \Rightarrow a=-2} \Rightarrow \bbox[red,2pt]{-2 \le a\le 6}$$

解：$$\log (\sqrt[3]{49})^{100} =100\log \sqrt[3]{49} ={100\over 3}\log 49 ={200\over 3}\log 7 ={200\over 3}\times 0.8451 = 56.34 \Rightarrow n=56\\ 又 \log 2=0.301 \lt 0.34 \lt  0.4771=\log 3 \Rightarrow m=2\\ 因此(m,n)=\bbox[red,2pt]{(2,56)}$$

解：

$$面積=1個正方形+4個等腰直角\triangle = (2+\sqrt 2)^2 + 4\times ({1\over 2}\times 1\times 1) =\bbox[red,2pt]{8+4\sqrt 2}$$

解：

$$\cos \angle BAC ={\overline{AB}^2 +\overline{AC}^2 -\overline{BC}^2 \over 2\cdot \overline{AB}\cdot \overline{AC}} \Rightarrow {1\over 3} = {96+96  -\overline{BC}^2 \over 2\cdot 96}  \Rightarrow \overline{BC}=8\sqrt 2 \\ 令O為\overline{BC} 中點 \Rightarrow \overline{AC}^2=\overline{AO}^2+ \overline{CO}^2 \Rightarrow 96=\overline{AO}^2 +(4\sqrt 2)^2 \Rightarrow \overline{AO}=8\\ \triangle DBC為等腰\triangle \Rightarrow \overline{CD}^2 = \overline{DO}^2 +\overline{CO}^2 \Rightarrow 8^2=\overline{DO}^2+ (4\sqrt 2)^2 \Rightarrow \overline{DO}=4\sqrt 2\\ 令\cases{O(0,0,0)\\ B(-4\sqrt 2,0,0)\\ C(4\sqrt 2, 0,0)\\ A(0,8,0)\\ D(0,a,b)}，由\cases{\overline{DO}=4\sqrt 2\\ \overline{DA}=4\sqrt 6} \Rightarrow \cases{a^2+b^2=32\\ (a-8)^2+b^2=96} \Rightarrow \cases{a=0\\ b=\pm 4\sqrt 2} \\ \Rightarrow D至\triangle ABC距離=\overline{OD}=|b|=\bbox[red,2pt]{4\sqrt 2}$$

----------- 

解題僅供參考，其他歷屆試題及詳解