110 學年度身心障礙學生升學大專校院甄試
甄試類(群)組別: 四技二專組-數學(B)
解答:$$(a,b)在第二象限 \Rightarrow \cases{a\lt 0\\ b\gt 0} \Rightarrow \cases{b-a \gt 0\\ {b\over a} \lt 0} \Rightarrow (b-a,{b\over a})在第四象,故選\bbox[red, 2pt]{(D)}$$
解答:$$(A)\bigcirc: (3,-4)\cdot (4,3)=0\\(B)\times :(3,4)\cdot (4,3)=24 \ne 0\\(C)\times:(4,-3)\times (4,3)=7 \ne 0\\(D)\times: (4,3)\cdot (4,3)=25 \ne 0\\,故選\bbox[red, 2pt]{(A)}$$
解答:$$\sin(540^\circ -30^\circ)-\cos(1080^\circ +60^\circ)+ \tan(810^\circ+ 45^\circ)= \sin(510^\circ )-\cos(1140^\circ )+\tan(855^\circ ) \\=\sin(360^\circ +150^\circ )-\cos(360^\circ\times 3+60^\circ )+\tan(360^\circ \times 2+135^\circ ) \\= \sin 150^\circ-\cos 60^\circ+\tan 135^\circ = {1\over 2}-{1\over 2}-1=-1,故選\bbox[red, 2pt]{(B)}$$
解答:$$(2\vec i-3\vec j-7\vec k)\cdot (5\vec i+4\vec j-\vec k) = 2\cdot 5+(-3)\cdot 4+(-7)\cdot (-1)=10-12+7=5,故選\bbox[red, 2pt]{(C)}$$解答:$$\cases{3^{y+2}-2^x+3=0 \\ 3^{-y}-2^{x+1}-1=0} \Rightarrow \cases{ 2^x=9\cdot3^{y}+3 \cdots(1)\\ {1\over 3^{y}}-2\cdot 2^{x}-1=0 \cdots(2)} ,將(1)代入(2) \Rightarrow {1\over 3^{y}}-2(9\cdot3^{y}+3)=1\\ \Rightarrow {1\over 3^y}-18\cdot 3^y=7 \Rightarrow 18\cdot (3^y)^2+7\cdot 3^y-1=0 \Rightarrow (9\cdot 3^y-1)(2\cdot 3^y+1)=0 \\ \Rightarrow 3^y={1\over 9}(3^y\ne -{1\over 2},\because 3^y \gt 0) \Rightarrow y=-2代回(1) \Rightarrow 2^x=1+3=4 \Rightarrow x=2 \\ \Rightarrow a+b= x+y = 2-2=0,故選\bbox[red, 2pt]{(B)}$$
解答:$$\log_7 49+ 100^{\log_{10}3}-\log_{1/4}64 = \log_77^2 + 10^{2\log_{10}3} +\log_4 4^3 =2+9+3 = 14,故選\bbox[red, 2pt]{(C)}$$
解答:$$\cases{弧長=r\theta\\ 扇形面積=r^2\pi\times{\theta \over 2\pi}} \Rightarrow 弧長與扇形面積皆與夾角成正比;\\又三弧長總和為1,三扇形面總和也為1,因此最大扇形面積=最長的弧長;\\現在三弧長a_1,a_2,a_3成等差,即a_1+a_2+a_3=a_1+a_1+d+a_1+2d = 3(a_1+d)=1\\ \Rightarrow a_1+d=1/3 \Rightarrow a_1+{1\over 4}={1\over 3} \Rightarrow a_1={1\over 12} \Rightarrow a_3={1\over 12}+2\times {1\over 4} ={7\over 12}\\ 因此可得最大扇形面積=最長的弧長={7\over 12},故選\bbox[red, 2pt]{(B)}$$
解答:$$\cases{a_3=12\\ a_4=24} \Rightarrow 公比r=a_4/a_3=2 \Rightarrow a_3=a_1r^2 = 4a_1=12 \Rightarrow a_1=3\\ \Rightarrow a_8=a_1r^7 = 3\times 2^7 = 384,故選\bbox[red, 2pt]{(A)}$$
解答:$$f(x)=2(x^2-1) +3(x+1)(x-2)+4(x-2)(x-1)+5 \\ \Rightarrow f(2)=2\times 3+0+0+5 = 11,故選\bbox[red, 2pt]{(D)}$$
解答:$$\begin{vmatrix} a & 1 & 4\\ b& 2 & 5\\ c& 3 &6\end{vmatrix} =\begin{vmatrix} a & 1 & 2\\ b& 2 & 1\\ c& 3 &0\end{vmatrix} = -3(a-2b+c) =3 \Rightarrow a-2b+c=-1\\ 因此\begin{vmatrix} a & b & c\\ 1& 1 & 1\\ 1& 2 &3\end{vmatrix} =\begin{vmatrix} a & b & c\\ 1& 1 & 1\\ 0& 1 &2\end{vmatrix} = a-2b+c = -1,故選\bbox[red,2pt]{(C)}$$
解答:$$f(x)=-9x^2 +24x-16 =-(3x-4)^2 \\(A)\bigcirc: f(x)\ge 0\Rightarrow x=4/3\\(B)\times: f(x)\le 0 \Rightarrow 無限多組解\\ (C)\times: f(x)\gt 0\Rightarrow 無解\\ (D)\times:f(x) \lt 0 \Rightarrow x\ne 4/3\\,故選\bbox[red,2pt]{(A)}$$
解答:
$$\cases{第一象限\\ 2x+y \le 8\\ x+2y\le 6} 所圍區域頂點坐標\cases{A(0,0)\\ B(4,0)\\ C(10/3,4/3)\\ D(0,3)} \Rightarrow \cases{f(A)=0\\ f(B)=-4\\ f(C)=-2\\ f(D)=3} \Rightarrow 最大值為3,故選\bbox[red,2pt]{(B)}$$
解答:$$a+b+c=20且a,b,c\ge 4 \Rightarrow a+b+c=8 ,其中a,b,c均為非負整數\\ 共有H^3_8=C^{10}_8=45組解,故選\bbox[red,2pt]{(D)}$$
解答:$$小於2的情形:(1,1),(1,2),(2,1),(2,2),(2,3),(3,2),(3,3),(3,4),(4,3),(4,4),(4,5),\\(5,4),(5,5),(5,6), (6,5),(6,6),共16種,機率為{16\over 36};因此大於等於2的機率為1-{16\over 36}={20\over 36};\\公平起見,兩者期望值需相等,即100\times {16\over 36} =x\times {20\over 36} \Rightarrow x=80,故選\bbox[red,2pt]{(A)}$$
解答:$$全距=最大-最小,故選\bbox[red,2pt]{(C)}$$
解答:$$\Omega=\{26,22,25,29,23,25\} \Rightarrow \bar x=(26+22 +25+29+23+25)\div 6=25 \\\Rightarrow 樣本標準差=s(x)=\sqrt{\sum_{i=1}^6 (x_i-\bar x)^2 \over 6-1} = \sqrt{1^2+ 3^2+0+4^2+2^2 +0 \over 5} =\sqrt{6},故選\bbox[red,2pt]{(D)}$$
解答:$$\sin\theta -\cos \theta = {1\over 3} \Rightarrow (\sin\theta -\cos \theta)^2={1-2\sin\theta \cos \theta} = {1\over 9} \Rightarrow 2\sin\theta \cos \theta = {8\over 9}\\ \Rightarrow {1\over 2}(\tan \theta+\cot \theta) ={1\over 2}\left({\sin \theta \over \cos \theta}+{\cos \theta\over \sin \theta}\right) = {1\over 2}\left({\sin^2 \theta+\cos^2\theta \over \sin\theta\cos \theta} \right) ={1\over 2}\left({1 \over \sin\theta\cos \theta} \right)\\ ={1\over 8/9}={9\over 8},故選\bbox[red, 2pt]{(A)}$$
解答:$$圓(x-2)^2+(y-3)^2 = 144 \Rightarrow \cases{圓心O(2,3)\\ 半徑r=12} \\令切點為Q,則\triangle OPQ為一直角三角形(\angle OQP=90^\circ) \Rightarrow \overline{PQ}^2 =\overline{OP}^2-\overline{OQ}^2 \\= (-3-2)^2+(-9-3)^2 -r^2 =25+144-144= 25 \\\Rightarrow \overline{PQ}=5,故選\bbox[red,2pt]{(C)}$$
解答:$$\lim_{n\to \infty}{2^{n+1} +5^{n-1} \over 2^{n} +5^{n}} =\lim_{n\to \infty}{2\cdot ({2\over 5})^{n+1} +{1\over 5} \over ({2\over 5})^{n} +1} = {0+{1\over 5} \over 0+1} ={1\over 5},故選\bbox[red, 2pt]{(D)}$$
解答:$$\cases{\int_2^7 f(x)\;dx=3\\ \int_7^2g(x)\;dx=4} \Rightarrow \int_2^7 [3f(x)+2g(x)]dx =3\int_2^7f(x)\;dx-2\int_7^2g(x)\;dx \\= 3\times 3-2\times 4=1,故選\bbox[red, 2pt]{(B)}$$
解答:$$小於2的情形:(1,1),(1,2),(2,1),(2,2),(2,3),(3,2),(3,3),(3,4),(4,3),(4,4),(4,5),\\(5,4),(5,5),(5,6), (6,5),(6,6),共16種,機率為{16\over 36};因此大於等於2的機率為1-{16\over 36}={20\over 36};\\公平起見,兩者期望值需相等,即100\times {16\over 36} =x\times {20\over 36} \Rightarrow x=80,故選\bbox[red,2pt]{(A)}$$
解答:$$全距=最大-最小,故選\bbox[red,2pt]{(C)}$$
解答:$$\Omega=\{26,22,25,29,23,25\} \Rightarrow \bar x=(26+22 +25+29+23+25)\div 6=25 \\\Rightarrow 樣本標準差=s(x)=\sqrt{\sum_{i=1}^6 (x_i-\bar x)^2 \over 6-1} = \sqrt{1^2+ 3^2+0+4^2+2^2 +0 \over 5} =\sqrt{6},故選\bbox[red,2pt]{(D)}$$
解答:$$\sin\theta -\cos \theta = {1\over 3} \Rightarrow (\sin\theta -\cos \theta)^2={1-2\sin\theta \cos \theta} = {1\over 9} \Rightarrow 2\sin\theta \cos \theta = {8\over 9}\\ \Rightarrow {1\over 2}(\tan \theta+\cot \theta) ={1\over 2}\left({\sin \theta \over \cos \theta}+{\cos \theta\over \sin \theta}\right) = {1\over 2}\left({\sin^2 \theta+\cos^2\theta \over \sin\theta\cos \theta} \right) ={1\over 2}\left({1 \over \sin\theta\cos \theta} \right)\\ ={1\over 8/9}={9\over 8},故選\bbox[red, 2pt]{(A)}$$
解答:$$圓(x-2)^2+(y-3)^2 = 144 \Rightarrow \cases{圓心O(2,3)\\ 半徑r=12} \\令切點為Q,則\triangle OPQ為一直角三角形(\angle OQP=90^\circ) \Rightarrow \overline{PQ}^2 =\overline{OP}^2-\overline{OQ}^2 \\= (-3-2)^2+(-9-3)^2 -r^2 =25+144-144= 25 \\\Rightarrow \overline{PQ}=5,故選\bbox[red,2pt]{(C)}$$
解答:$$\lim_{n\to \infty}{2^{n+1} +5^{n-1} \over 2^{n} +5^{n}} =\lim_{n\to \infty}{2\cdot ({2\over 5})^{n+1} +{1\over 5} \over ({2\over 5})^{n} +1} = {0+{1\over 5} \over 0+1} ={1\over 5},故選\bbox[red, 2pt]{(D)}$$
解答:$$\cases{\int_2^7 f(x)\;dx=3\\ \int_7^2g(x)\;dx=4} \Rightarrow \int_2^7 [3f(x)+2g(x)]dx =3\int_2^7f(x)\;dx-2\int_7^2g(x)\;dx \\= 3\times 3-2\times 4=1,故選\bbox[red, 2pt]{(B)}$$


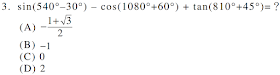

















沒有留言:
張貼留言