111年新北市國中教甄聯招-數學詳解

新北市立國民中學 111 學年度教師聯合甄選

選擇題： 共 40 題， 總分 100 分。 每題 2.5 分

解答：$$99=3\times 3\times 11、98=2\times 7\times 7, 97質數、96=2^5\times 3、95=5\times 19、94 = 2\times 47\\ 93=3\times 31、92=2\times 2\times 23、 91=7\times 13、90=2\times 3\times 3\times 5  ，故選\bbox[red,2pt]{(D)}$$

解答：$$令\cases{a=x-111\\ b=x-115} \Rightarrow \cases{a^2+b^2 = 100\\ a-b= 4} \Rightarrow (a-b)^2 = 100-2ab= 16 \Rightarrow ab=42，故選\bbox[red,2pt]{(B)}$$

解答：$$\sqrt a+ \sqrt b = \sqrt{180} =6\sqrt 5 \Rightarrow c\sqrt 5+ d\sqrt 5= 6\sqrt 5，其中\cases{a=5c^2 \\ b=5d^2}\\ \Rightarrow c+d= 6的非負整數解個數=H^2_6=C^7_6=7，故選\bbox[red,2pt]{(B)}$$

解答：$$3^{23}=(3^2)^{11.5} =9^{11.5} \gt 8^{11}\\ \cases{3^{23}=(3^3)^{7.6}= 27^{7.6}\\ 5^{14}=(5^2)^7=25^7} \Rightarrow 3^{23}\gt 5^{14}\\ 3^{23} \gt (3^{2.5})^9 =(9\sqrt 3)^9 = (9\times 1.732)^9 \gt 11^9\\ 由上可知: 3^{23}最大，故選\bbox[red,2pt]{(A)}$$

解答：$$f(1)=f(9) \gt f(10) \Rightarrow \cases{y=f(x)圖形為凹向下\\ 極大值為f((9+1)\div 2)= f(5)} \\(A)\times: |3-5|\lt |8-5| \Rightarrow 3比8更接近5\Rightarrow f(3)\gt f(8) \\(B)\times: |0-5|\lt |11-5| \Rightarrow 0比11更接近5 \Rightarrow f(0)\gt f(11) \\(C)\times: 無法判定極大值f(5)是否\ge 0，因此無法判定是有相異實根\\ (D)\bigcirc: {-b\over 2a}=5 \gt 0 \Rightarrow ab\lt 0\\，故選\bbox[red,2pt]{(D)}$$

解答：$$本題\bbox[red,2pt]{送分}$$

解答：$$(A) |x-4|\ge |x+5| \Rightarrow (x-4)^2 \ge (x+5)^2 \Rightarrow x\le -{1\over 2} 有無窮多個整數解\\ (B)同理，有無窮多個整數解\\ (C)(3x-5)^2 \ge (8x-2)^2 \Rightarrow 55x^2-2x-21\le 0 \Rightarrow (11x-7)(5x+3)\le 0 \Rightarrow -{5\over 3} \le x\le {11\over 7}\\ \qquad \Rightarrow x=-1,0,1，有三個整數解\\ (D)也是無窮多個整數解\\，故選\bbox[red,2pt]{(C)}$$

解答：$$此題相當於求a^2+b^2 有多少不同的數字，其中a,b\in \mathbb{Z}，且0\le a,b\le 6\\ 由於a^2,b^2 \in [0,1^2,2^2,\dots, 6^2]，有7種不同的數字，共有C^7_2+7(可重複)=28種組合\\，其中a=b=0不合(需相異兩點)，又3^2+4^2 =0^2+5^2((0,0)至(3,4)的距離=(0,0)至(5,0))\\ 因此共有28-2=26種不同的長度，故選\bbox[red,2pt]{(A)}$$

解答：$${(n+1-2)180 \over n+1} = {(n-1-2)180 \over n-1}+2 \Rightarrow {(n-1)180 \over n+1} = {(n-3)180 \over n-1}+2 \\\Rightarrow 180(n-1)^2 = 180(n+1)(n-3) +2(n^2-1) \Rightarrow 2n^2 = 722 \Rightarrow n=19，故選\bbox[red,2pt]{(B)}$$

解答：$$\cases{a_8=a_{8+4k} =3 \Rightarrow a_{100}= a_{8+4\cdot 23} =3\\ a_{22}= a_{22+4m}=15 \Rightarrow a_{102}=15\\ a_{31}= a_{31+4n}=18 \Rightarrow a_{103}=18} \Rightarrow a_{100}+a_{101}+ a_{102}+ a_{103}=55\\ \Rightarrow 3+a_{101}+ 15+18 = 55 \Rightarrow a_{101}=55-18\cdot 2= 19，故選\bbox[red,2pt]{(D)}$$

解答：$$x+2y +3z=4 \Rightarrow \vec u=(1,2,3) \Rightarrow |\vec u|=\sqrt{14}\\ (A) 3x+2y=1 \Rightarrow \vec v=(3,2,0) \Rightarrow \cos \theta ={\vec u\cdot \vec v \over |\vec u||\vec v|} ={7\over \sqrt{13\cdot 14}} \\(B)2y+z=2 \Rightarrow \vec v=(0,2,1) \Rightarrow \cos \theta ={\vec u\cdot \vec v \over |\vec u||\vec v|} ={7\over \sqrt{5\cdot 14}} \\(C)3x+z =3 \Rightarrow \vec v=(3,0,1) \Rightarrow \cos \theta ={\vec u\cdot \vec v \over |\vec u||\vec v|} ={6\over \sqrt{10\cdot 14}} \\(D)2x+y+ z=4 \Rightarrow \vec v=(2,1,1)  \Rightarrow \cos \theta ={\vec u\cdot \vec v \over |\vec u||\vec v|} = {7\over \sqrt{6\cdot 14}}\\(C)值最小，故選\bbox[red,2pt]{(C)}$$

解答：$$\cases{a\sqrt a+ b\sqrt b= 50\cdots(1)  \\ a\sqrt b+ b\sqrt a= 25 \cdots(2) }\Rightarrow  {(1)\over (2)} = {(\sqrt a)^3 + (\sqrt b )^3  \over \sqrt a\cdot \sqrt{ab}+ \sqrt b  \cdot \sqrt{ab}} ={(\sqrt a+\sqrt b)(a-\sqrt{ab}+b) \over   \sqrt{ab} (\sqrt a+\sqrt b) }\\ ={a-\sqrt{ab}+b \over \sqrt{ab}}={50\over 25} =2 \Rightarrow a+b=3\sqrt{ab} \Rightarrow a^2+b^2 =7ab \cdots(3)\\ 又(1)\times (2) =(a\sqrt a+ b\sqrt b)(a\sqrt b+ b\sqrt a )= a^2\sqrt{ab}+a^2b+ ab^2+ b^2\sqrt{ab} \\=\sqrt{ab}(a^2+b^2)+ab(a+b)=1250 \cdots(4)\\ 將(3)代入(4)\Rightarrow \sqrt{ab}(7ab)+ab(3\sqrt{ab})=1250 \Rightarrow 10 ab\sqrt{ab}=1250 \Rightarrow ab\sqrt{ab}=125\\ \Rightarrow (\sqrt {ab})^3=125  \Rightarrow \sqrt {ab}=5 \Rightarrow ab=25，故選\bbox[red,2pt]{(A)}$$

解答：$$\cases{4x+3y =a\\ 3x+6y=b } \Rightarrow \cases{x=(2a-b)/5\\ y=(4b-3a)/15} \Rightarrow x+y = {3a+b\over 15}\\ \Rightarrow \begin{array}{} a& b& 2a+b \\\hline 1 & 12 & 14\\ 2& 9 & 13 \\ 3& 6 & 12 \\ 4& 3 & 11\\\hline\end{array} \Rightarrow 2a+b=11 為最小值，故選\bbox[red,2pt]{(C)}$$

解答：$$x+2, 2x+1, y,8x-101成等比數列\Rightarrow {2x+1\over x+2} ={y\over 2x+1} ={8x-101\over y} \\ \Rightarrow \cases{(2x+1)^2 = y(x+2)\\ y^2=(2x+1)(8x-101)} \Rightarrow y^2 ={(2x+1)^4 \over (x+2)^2} = (2x+1)(8x-101)\\ \Rightarrow (2x+1)^3 = (x+2)^2 (8x-101) \Rightarrow 8x^3+12x^2+6x+1 = 8x^3-69x^2-372x-404\\ \Rightarrow 27(3x^2+14x+15)=0 \Rightarrow 27(x+3)(3x+5)=0 \\\Rightarrow \cases{x=-3 \Rightarrow y=(2x+1)^2/(x+2)= -25\\ x=-5/3非整數，不合}，故選\bbox[red,2pt]{(A)}$$

解答：

$$本題相當於求正十邊形內切圓的半徑長，依題\cases{\overline{AB}=1 \\\angle OAB={360^\circ \over 10}=36^\circ} \\ \Rightarrow \cases{M=\overline{AB} 中點\\ \angle OBM=18^\circ} \Rightarrow \tan 18^\circ ={1/2\over R} \Rightarrow R={1\over 2\tan 18^\circ} ={\cot 18^\circ \over 2}，故選\bbox[red,2pt]{(D)}$$

解答：$${A廠生產的瑕疵品\over A廠生產的瑕疵品+ B廠生產的瑕疵品} ={60\%\times 5\%\over 60\%\times 5\% +40\%\times 3\%} ={3\%\over 3\% + 1.2\%} \\={1\over 1.4} = {5\over 7}，故選\bbox[red,2pt]{(B)}$$

解答：

$$內切圓面積=r^2\pi =4\pi \Rightarrow 內切圓半徑=2，由上圖可知:(a+5)^2 = 7^2+(a+2)^2 \Rightarrow a={14\over 3}\\ \Rightarrow 三角形面積={1\over 2}\cdot 7\cdot (a+2) ={7\over 2}\cdot {20\over 3} ={70\over 3}，故選\bbox[red,2pt]{(A)}$$

解答：$$擲骰子三次點數分別為a,b,c，依題意需同時滿足\cases{b\gt a\\ b\gt c}，因此\\ \begin{array}{}b & a,c排列數\\\hline 2 & 1\\   3 & 2^2=4\\  4& 3^2=9\\ 5 & 4^2 =16 \\ 6 & 5^2 = 25\\\hdashline \end{array} ，共有1+ 4+ 9 +16+25=55種可能，機率為{55\over 6^3} \approx 0.255，故選\bbox[red,2pt]{(D)}$$

解答：

$$\cases{\overline{DF}={1\over 2}\overline{AB}=6\\ \angle ADB=90^\circ } \Rightarrow F為\triangle ABD外接圓圓心 \Rightarrow \overline{FB}=\overline{FA}= \overline{FD}=6 \\ 因此\cfrac{\overline{BE}}{\overline{EC}}=\cfrac{\overline{BF}}{\overline{FA}} \Rightarrow \overline{EF}\parallel \overline{AC} \Rightarrow \cfrac{\overline{EF}}{\overline{AC} }= {1\over 2} \Rightarrow \overline{EF}={1\over 2}\cdot 14=7，故選\bbox[red,2pt]{(C)}$$

解答：$$7班選4班有C^7_4取法，而每一班各有2種選法，因此共有2^4C^7_4取法，機率為{2^4C^7_4\over c^{14}_4} ={80\over 143}\\，故選\bbox[red,2pt]{(B)}$$

解答：$$每人有四種可能:都不買、買A不買B、買B不買A、AB都買，因此有4^4=256種情形；\\狀況一:\cases{四人都不買A:2^4=16\\ 四人都不買B:2^4=16}，扣除既不買A也不買B，共有16+16-1=31種情形\\ 狀況二:四人都有買A:2^4=16\\ 狀況一與狀況二的交集:四人都有買A且四人都沒買B，這只有一種情形；\\因此狀況一聯集狀況二的情形有46種；\\總共有256-46=210購買情形，故選\bbox[red,2pt]{(C)}$$

解答：$$假設f(x)=ax^3+ bx^2 +cx+d \Rightarrow \cases{f(0)=d=1\\ f(-1)=-a+b-c+d=0} \Rightarrow \cases{d=1\\ a-b+c=1} \cdots(1)\\ \Rightarrow (x+1)f(x)= ax^4+ (a+b)x^3+ (b+c)x^2+ (c+1)x +1\\ 由長除法可得 (x+1)f(x)=(x^3+x^2 +x+1) (ax+b)+ (c-a)x^2 + (-a-b+c+1)x+ 1-b\\ \Rightarrow \cases{c-a=1\\ -a+c+1-b=0\\ 1-b=-1}再加上(1)，可得\cases{a=1\\ b=c=2 \\d=1}\\ \Rightarrow f(x)= x^3 +2x^2 +2x+1 \Rightarrow f(1)= 1+2+2+1 = 6，故選\bbox[red,2pt]{(A)}$$

解答：$$\cases{A(1,0)\\ B(1,2)\\ C(0,a)} \Rightarrow \cases{\overline{AC}= \sqrt{a^2+1}\\ \overline{BC}= \sqrt{(a-2)^2+1}}\Rightarrow \cfrac{\overline{AC}} {\overline{BC}} =\sqrt{a^2+1\over (a-2)^2+1}=\sqrt {a^2+1\over a^2-4a+5} \\ 假設f(a)={a^2+1\over a^2-4a+5},本題欲求\sqrt{f(a)}之極值,因此先求f(a)之極值\\ f'(a)={2a \over a^2-4a+5} -{ (a^2+1)(2a-4)\over (a^2-4a+5)^2} ={ -4(a^2-2a-1)\over (a^2-4a+5)^2}\\ 因此f'(a)=0 \Rightarrow a^2-2a-1=0 \Rightarrow a=1+\sqrt 2 \Rightarrow f(1+\sqrt 2)= 3+2\sqrt 2 \\ \Rightarrow 欲求之極值 \sqrt{f(1+\sqrt 2)}= \sqrt 2+1，故選\bbox[red,2pt]{(D)}$$

解答：$$Y=a+b(X-65) \Rightarrow \cases{a=英文平均分數=50\\ b= r_{xy}\cdot {\sigma_Y\over \sigma_X} =0.75\cdot {12\over 9}=1} \Rightarrow a+b=50+1=51，故選\bbox[red,2pt]{(A)}$$

解答：$$\cases{A(0,1)\\ B(1/2,0)\\ C(1,1)\\ D(0,3)} \Rightarrow \cases{\overline{AB}= \overline{BC}= \sqrt{5\over 4}\\ \overline{CD}= \sqrt 5} \Rightarrow \overline{AB}+ \overline{BC}+ \overline{CD}= 2\sqrt 5，故選\bbox[red,2pt]{(C)}$$

解答：$$令\cases{A=10^{21}+111\\ B=10^7+5}，由於(10^7+5)(10^{14}-5\times 10^7)=10^{21}-25\times 10^7 \\\Rightarrow A+25\times 10^7=B(10^{14}-5\times 10^7)；又24B \lt 25\times 10^7 \lt 25B\\ 因此\lfloor A\div B \rfloor=   (10^{14}-5\times 10^7)+24 =m \Rightarrow m = 24 \mod 100，故選\bbox[red,2pt]{(A)}$$

解答：

$$令\cases{\angle CAD=\alpha \\ \angle C=\theta \\ \overline{AC}=x \\ \overline{AB}=\overline{CD}=a}，則\cases{\triangle ACD: \cfrac{x}{ \sin(180^\circ-(\alpha+\theta))} =\cfrac{x}{ \sin( \alpha+\theta)} =\cfrac{a}{ \sin \alpha}\\[1ex] \triangle ABC:\cfrac{x}{\sin 2\theta}=\cfrac{a}{\sin\theta}}\\ \Rightarrow x=\cfrac{a\sin(\alpha+\theta)}{\sin \alpha} =\cfrac{a\sin 2\theta}{\sin \theta } =2a\cos \theta \Rightarrow \sin(\alpha+\theta)=2\sin \alpha \cos \theta \Rightarrow \sin \theta\cos \alpha= \sin \alpha\cos \theta\\ \Rightarrow \sin(\theta-\alpha)=0 \Rightarrow \theta=\alpha \Rightarrow 72^\circ+4\theta=180^\circ  \Rightarrow \theta = 27^\circ ，故選\bbox[red,2pt]{(C)}$$

解答：

$$\overline{AD}=40\Rightarrow \cases{\overline{BD}=20\\ \overline{AB}=20\sqrt 3} \Rightarrow \overline{CD}=\overline{AB}-\overline{BD}=20(\sqrt 3-1) \Rightarrow \overline{EC} =\overline{ED}= \overline{CD}\div \sqrt 2\\ =10(\sqrt 6-\sqrt 2) \Rightarrow \overline{AE}= \overline{AC}-\overline{EC} = \sqrt 2\overline{AB}-10(\sqrt 6-\sqrt 2)=20\sqrt 6-10(\sqrt 6-\sqrt 2)\\ =10\sqrt 6+10\sqrt 2 \Rightarrow \overline{AE}-\overline{ED}= (10\sqrt 6+10\sqrt 2)-10(\sqrt 6-\sqrt 2) =20\sqrt 2 = 28.28，故選\bbox[red,2pt]{(D)}$$

解答：

$$假設\cases{G= \overleftrightarrow{AB'} \cap \overline{BC}\\ H= \overleftrightarrow{AC'} \cap \overline{BC}} \Rightarrow \cases{\overline{BB'}為\overline{AG}的中垂線\\ \overline{CC'}為\overline{AH}的中垂線} \Rightarrow \cases{\overline{BA}=\overline{BG} = 68\\ \overline{CH}=\overline{CA} =76} \Rightarrow \cases{\overline{CG}=92-68=24\\ \overline{BH}=92-76=16} \\  \Rightarrow \overline{HG}=92-24-16=52 \\由於\cfrac{\overline{AC'}}{\overline{AH}} =\cfrac{\overline{AB'}}{\overline{AG}} = {1\over 2}\Rightarrow \overline{B'C'}={1\over 2}\overline{HG}=26，故選\bbox[red,2pt]{(C)}$$

解答：$$假設直圓錐\cases{底面圓半徑 r\\高h\\斜邊高s=\sqrt{r^2+h^2}} \Rightarrow 側表面積=\pi r s ，\\因此原直圓錐h=r  \Rightarrow s= \sqrt 2r \Rightarrow 側表面積=\sqrt 2\pi r^2\\ (A)s=\sqrt{r^2+(2.5r)^2}=\sqrt{7.25}r \Rightarrow 側表面積=\sqrt{7.25}\pi r^2\\ (B)s = \sqrt{r^2+(1.5r)^2} =\sqrt{3.25}r \Rightarrow 側表面積=\pi\cdot 1.5r\cdot \sqrt{3.25}r =1.5\sqrt {3.25}\pi r^2 \\(C)s=\sqrt{(1.1r)^2 +(2r)^2} =\sqrt{5.21}r \Rightarrow 側表面積=\pi \cdot 1.1r\cdot \sqrt{5.21}r = 1.1\sqrt {5.21}\pi r^2 \\(D)原角度={2\pi r\over s}={2\pi r\over \sqrt 2r} =\sqrt 2\pi  \Rightarrow 新角度={\sqrt 2\over 1.19}\pi  \Rightarrow s=\cfrac{2\pi r}{\sqrt 2\pi/ 1.19} =1.19\sqrt 2 r\\ \qquad \Rightarrow 側表面積= 1.19\sqrt 2 \pi r^2\\ (B)值最大，故選\bbox[red,2pt]{(B)}$$

解答：$$90-100分占全體的(100\%-84\%)=16\% \Rightarrow 全體有80\div 16\%=500人\\\cases{70-80占全校23\%\\ 成績80分的累積相對次數為60\%} \Rightarrow 成績70分的累積相對次數為60\%-23\%=37\%\\ \Rightarrow 60-70分占全體的37\%-28\% = 9\% \Rightarrow 人數為500\times 9\%= 45人，故選\bbox[red,2pt]{(C)}$$

解答：$$由盒狀圖可知\overline{Q_1Q_2}\lt \overline{Q_2Q_3}，只有(B)符合此條件，故選\bbox[red,2pt]{(B)}$$

解答：$$直線L:x+ay=2+4a \Rightarrow x-2=-a(y-4) \Rightarrow L通過P(2,4);\\ f(x)=x^3-6x^2+15x-10 \Rightarrow f'(x)=3x^2-12x+15 \Rightarrow f''(x)=6x-12\\ 因此f''(x)=0 \Rightarrow x=2 \Rightarrow P為圖形y=f(x)的對稱中心 \Rightarrow \cases{b_1+b_2+b_3= 3\cdot 2=6\\ c_1+c_2+c_3= 3\cdot 4=12} \\ \Rightarrow b_1+b_2+b_3 +c_1+c_2+c_3 =6+12=18，故選\bbox[red,2pt]{(A)}$$

解答：

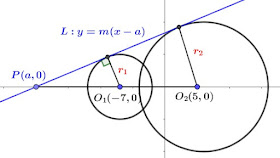
$$\cases{圓C_1:(x+7)^2+y^2=25 \Rightarrow \cases{圓心O_1(-7,0)\\ 半徑r_1=5}\\ 圓C_2: (x-6)^2+y^2=100 \Rightarrow \cases{圓心O_2(6,0)\\ 半徑r_2=10}};\\兩圓心皆在x軸線上，可假設公切線L經過P(a,0)；因此\cfrac{\overline{PO_1}}{\overline{PO_2}} =\cfrac{ \overline{r_1}}{ \overline{r_2}} \Rightarrow {-7-a\over 6-a}={5\over 10} \Rightarrow a=-20\\ \Rightarrow L: y=m(x+20) \Rightarrow d(O_1,L)=r_1 \Rightarrow \left| {13m\over \sqrt{m^2+1}}\right|=5 \Rightarrow m={5\over 12}(斜率需為正值)\\ \Rightarrow L:y={5\over 12}(x+20) \Rightarrow \cases{(A)x=12 \Rightarrow y=40/3\\(B)x=8 \Rightarrow y=35/3 \\(C) x=4\Rightarrow y=10 \\(D) x=0 \Rightarrow y=25/3}，故選\bbox[red,2pt]{(C)}$$

解答：$$取巧的方法，找變異數和最小的，即(C)或(D)，但(D)的多數(700人)變異數較小\\，合併後的變異數會比(C)小，故選\bbox[red,2pt]{(D)}$$

解答：$$假設地球半徑為R\\ (A) R\cos 60^\circ \times (135^\circ-100^\circ)={35\over 2}R =17.5R \\(B)R\cos 45^\circ \times (125^\circ-100^\circ) ={25\sqrt 2\over 2}R \approx 17.67R\\ (C)R\cos 30^\circ \times (120^\circ-100^\circ) = {20\sqrt 3\over 2}R \approx 17.32R\\(D) R\cos 0^\circ\times (117^\circ-100^\circ) = 17R\\ 因此選項(B)最大，故選\bbox[red,2pt]{(B)}$$

解答：$$假設\cases{A位於正方形的中心，即A(3.5,3.5)\\ B位於左上角頂點，即B(0,7)\\ C位於右下角頂點，即C(7,0)} \Rightarrow \cases{\overrightarrow{AB} = (-3.5,3.5)\\ \overrightarrow{AC} =(3.5,-3.5)} \\\Rightarrow \overrightarrow{AB}\cdot \overrightarrow{AC} =-3.5^2-3.5^2 =-24.5，故選\bbox[red,2pt]{(C)}$$

解答：$$\log E=4.8+1.5Q \Rightarrow E=10^{4.8}\cdot 10^{1.5Q} \Rightarrow {日本地震能量\over 集集地震能量} =\cfrac{10^{4.8}\cdot 10^{1.5\cdot 9.1} }{10^{4.8}\cdot 10^{1.5\cdot 7.3}} =10^{1.5(9.1-7.3)}\\ =10^{1.5\cdot 1.8}  =10^{2.7} \approx 500，故選\bbox[red,2pt]{(D)}$$

解答：$$A^5=A^3\cdot A^2 \Rightarrow A^2=(A^3)^{-1}A^5 = \left(\begin{bmatrix} 7 & 6 \\-6 & -5\end{bmatrix} \right)^{-1} \begin{bmatrix} 11 & 10\\ -10 & -9\end{bmatrix}  =  \begin{bmatrix} -5 & -6 \\ 6 & 7\end{bmatrix} \begin{bmatrix} 11 & 10\\ -10 & -9\end{bmatrix} \\=\begin{bmatrix} 5 & 4\\ -4 & -3\end{bmatrix} \Rightarrow \begin{bmatrix} 5 & 4\\ -4 & -3\end{bmatrix} A= \begin{bmatrix} 7 & 6 \\-6 & -5\end{bmatrix} \Rightarrow A=\left( \begin{bmatrix} 5 & 4\\ -4 & -3\end{bmatrix} \right)^{-1}\begin{bmatrix} 7 & 6 \\-6 & -5\end{bmatrix} \\ =\begin{bmatrix} -3 & -4\\ 4 & 5\end{bmatrix}  \begin{bmatrix} 7 & 6 \\-6 & -5\end{bmatrix} = \begin{bmatrix} 3 & 2 \\-2 & -1\end{bmatrix} =\begin{bmatrix} a & b \\c & d\end{bmatrix} \Rightarrow a^2+b^2+c^2+d^2 = 9+4+4+1=18\\，故選\bbox[red,2pt]{(A)}$$

解答：

$$L通過(4,0)及(12,144) \Rightarrow L:y=18x-72 \Rightarrow \cases{L與拋物線y=x^2交於A(12,144)及B(6,36)\\ L與x軸交於C(4,0)\\L與y軸交於D(0,-72)} \\ \Rightarrow 所求面積=\int_0^6 x^2-(18x-72)\;dx - \triangle OCD面積= \left. \left[ {1\over 3}x^3-9x^2+72x \right] \right|_0^6 -{1\over 2}\cdot 4\cdot 72\\ =180-144=36，故選\bbox[red,2pt]{(D)}$$

====================== END ======================

解題僅供參考，其他教甄歷年試題及詳解