112 學年度身心障礙學生升學大專校院甄試
甄試類(群)組別:四技二專組-數學(C)
單選題,共 20 題,每題 5 分
解答:$$\sin \theta+\cos\theta={1\over 3} \Rightarrow (\sin \theta+\cos\theta)^2=1+ 2\sin \theta \cos \theta ={1\over 9} \Rightarrow \sin 2\theta =2\sin \theta \cos \theta =-{8\over 9}\\,故選\bbox[red, 2pt]{(A)}$$
解答:$$f(x)=(2x-1)^6 \Rightarrow f'(x)=12(2x-1)^5 \Rightarrow f'(1)=12,故選\bbox[red, 2pt]{(B)}$$
解答:$$\cases{A(1,0,1)\\ B(0,1,2)\\ C(6,1,-2)} \Rightarrow \cases{\vec u=\overrightarrow{AB}=(-1,1,1) \\ \vec v=\overrightarrow{AC}=(5,1,-3)} \Rightarrow \vec n=\vec u\times \vec v=(-4,2,-6) \\ \Rightarrow E:-4(x-1)+2y-6(z-1)=0 \Rightarrow 2x-y+3z=5\\ \Rightarrow (2,-1,0)符合2x-y+3z=5,故選\bbox[red, 2pt]{(A)}$$
解答:$$\overline{AP}:\overline{PB}=2:1 \Rightarrow P=(2B+A)\div 3 = {(10,4)+(2,-1)\over 3} =(4,1),故選\bbox[red, 2pt]{(D)}$$
解答:$$(a,a,b),(a,b,a),(b,a,a)各有6\times 5=30種,共3\times 30=90種,故選\bbox[red, 2pt]{(B)}$$
解答:$$ =\int_0^4 (2x-1)\,dx = \left.\left[ x^2-x \right]\right|_0^4= 16-4=12,故選\bbox[red, 2pt]{(D)}$$
解答:$$\cases{x=\sqrt[3]{81} =\sqrt[3]{3^4} =3\sqrt[3] 3\\ y=\sqrt[4]{243} =\sqrt[4]{3^5} =3\sqrt[4]3 \\z=\sqrt{27} =3\sqrt 3} \Rightarrow z\gt x\gt y,故選\bbox[red, 2pt]{(B)}$$
解答:$$h(x)=f(x)g(x) \Rightarrow h'(x)=f'(x)g(x)+ f(x)g'(x) \Rightarrow h'(1)= f'(1)g(1)+ f(1)g'(1) \\ =4\cdot 3 + 2\cdot 9= 12+18=30,故選\bbox[red, 2pt]{(A)}$$
解答:$$\cases{A=\begin{bmatrix}2 & 3 & 4 \\ 3& 4 & 5\end{bmatrix}\\[1ex] B=\begin{bmatrix}0 & -1\\ 1& 0 \\ 2& 1\end{bmatrix}} \Rightarrow A\times B=\begin{bmatrix}11 &2 \\14 & 2\end{bmatrix},故選\bbox[red, 2pt]{(C)}$$
解答:$$\alpha,\beta 為x^2+2x+4=0的兩根\Rightarrow \cases{\alpha+ \beta=-2\\ \alpha\beta =4} \Rightarrow \alpha^2+\beta^2 =(\alpha+\beta)^2-2\alpha\beta=4-8=-4\\ \Rightarrow \alpha^3+\beta^3 = (\alpha+\beta) (\alpha^2-\alpha\beta+\beta^2)=(-2)(-4-4) =16,故選\bbox[red, 2pt]{(D)}$$
解答:$$\cases{4A+B\le 70\\ 2A+3B\le 60\\ 0\le A,B} 所圍區域頂點\cases{\alpha(0,20)\\ \beta(15,10) \\ \gamma(35/2,0)}\\令 f(A,B)=6A+5B,則\cases{f(\alpha)=100\\ f(\beta)=140最大\\ f(\gamma)= 175/2},故選\bbox[red, 2pt]{(D)}$$
解答:$$(1+i)^2 =2i \Rightarrow (1+i)^3=-2+2i \Rightarrow (1+i)^4=-4 \Rightarrow \sum_{k=1}^{4}(1+i)^k =(1+i)+2i+(-2+2i)-4 \\ =-5+5i,故選\bbox[red, 2pt]{(A)}$$
解答:$$100-(510\div 9)\times 0.03= 98.3,故選\bbox[red, 2pt]{(C)}$$
解答:$$\cases{\vec a\parallel \vec b \Rightarrow {2\over x+1}= {3\over 6} \Rightarrow x=3\\ \vec a\bot \vec c \Rightarrow \vec a\cdot \vec c=0 \Rightarrow 6+3y=0 \Rightarrow y=-2} \Rightarrow 2x+y= 6-2=4,故選\bbox[red, 2pt]{(C)}$$
解答:$$圓C:x^2+y^2=1 \Rightarrow \cases{圓心O(0,0) \\圓半徑r=1} \Rightarrow \overline{OA}=2 \Rightarrow 切線長=\sqrt{\overline{OA}^2-r^2} =\sqrt{4-1} =\sqrt 3\\,故選\bbox[red, 2pt]{(B)}$$
解答:$$假設A(0,0)\Rightarrow 颱風路行經路徑沿著直線L:x=200/\sqrt 2,由(200/\sqrt 2,-200/\sqrt 2)往北走\\ 當d(A,P)\gt 250時,A點離開暴風圈,其中P(200/\sqrt 2,k)\in L;\\d(A,P)= \sqrt{20000+k^2} \gt 250 \Rightarrow 20000 +k^2 \gt 62500 \Rightarrow k^2 \gt 42500 \Rightarrow k\gt 50\sqrt 7\\ \Rightarrow 移動距離=50\sqrt 7+200/\sqrt 2 \Rightarrow 移動時間=(50\sqrt 7+200/\sqrt 2)\div 30 \approx 9.1,故選\bbox[red, 2pt]{(A)}$$
解答:$$\cases{內切圓半徑=0.5\\ 外接圓半徑=\sqrt 2/2} \Rightarrow {A_1\over A_2}={0.5^2 \over (\sqrt 2/2)^2} ={1/4\over 1/2}={1\over 2},故選\bbox[red, 2pt]{(C)}$$
解答:$$S=1+2({1\over 3})+ 3({1\over 3})^2 +4({1\over 3})^3+ \cdots \Rightarrow {1\over 3}S= ({1\over 3})+ 2({1\over 3})^2+ 3({1\over 3})^3 +4({1\over 3})^4+\cdots \\ \Rightarrow S-{1\over 3}S= {2\over 3}S=1+{1\over 3}+ ({1\over 3})^2+({1\over 3})^3 +\cdots = {1\over 1-1/3}={3\over 2} \Rightarrow S={3\over 2}\cdot {3\over 2}={9\over 4}= 2.25\\,故選\bbox[red, 2pt]{(B)}$$
解答:$$a+b:b+c:c+a=9:11:12 \Rightarrow \cases{a+b=9k\\ b+c=11k\\ c+a=12k} \Rightarrow a+b+c=16k \Rightarrow \cases{c=7k\\ a=5k\\ b=4k} \\ \Rightarrow \cos \angle C={5^2+4^2-7^2\over 2\cdot 4\cdot 5} =-{1\over 5} \Rightarrow \sin \angle C={2\sqrt 6\over 5} \Rightarrow \triangle ABC面積={1\over 2}\cdot ab\sin \angle C \\=10k^2\cdot {2\sqrt 6\over 5} =8\sqrt 6 \Rightarrow k^2=2 \Rightarrow k=\sqrt 2\\ 內切圓半徑r={2\times \triangle面積\over a+b+c} ={16\sqrt 6\over 16\sqrt 2} =\sqrt 3 \Rightarrow 內切圓面積=r^2\pi =3\pi,故選\bbox[red, 2pt]{(C)}$$
================ END =================
解題僅供參考,其他歷年試題及詳解










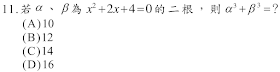









沒有留言:
張貼留言