112年身心障礙人員考試
考 試 別:身心障礙人員考試
等別:三等考試
類科:電力工程
科目:工程數學
甲、申論題部分:(50 分)
解答:$$y''+2y'+2y=\begin{cases} 10\sin(2t),& 0\lt t\lt 1\\ 0, & t\ge 1\end{cases} =10\sin(2t)-10\sin(2t)u(t-1)\\ \Rightarrow \mathcal L^{-1}\{y''+2y'+2y\} =\mathcal L^{-1}\{ 10\sin(2t)-10\sin(2t)u(t-1)\}\\ \Rightarrow s^2Y(s) -sy(0)-y'(0)+2(sY(s)-y(0)) + 2Y(s)={20\over s^2+ 4}-{10e^{-s}(s\sin 2+2\cos 2) \over s^2+4} \\ \Rightarrow (s^2+ 2s+2)Y(s)-s+3 ={20\over s^2+ 4}-{10e^{-s}(s\sin 2+2\cos 2) \over s^2+4} \\ \Rightarrow Y(s)={20\over (s^2+ 4)(s^2+2s+2)}-{10e^{-s}(s\sin 2+2\cos 2) \over (s^2+4)(s^2+2s+2)} +{s-3\over s^2+2s+2}\\ \mathcal L^{-1}\{{20\over (s^2+ 4)(s^2+2s+2)}\} =\mathcal L^{-1}\{{-2s-2\over ( s^2+4}+ 2{s+1\over (s+1)^2+1}+ 4{1\over (s+1)^2+1}\}\\\quad =-2 \cos(2t)-\sin(2t)+2e^{-t}(\cos t+2\sin t) \\\mathcal L^{-1}\{{s-3 \over s^2+2s+2}\} =\mathcal L^{-1}\{{s+1 \over (s+1)^2+1} -{4\over (s+1)^2+1}\} =e^{-t}(\cos t-4\sin t) \\ \mathcal L^{-1}\{{10e^{-s}(s\sin 2+2\cos 2) \over (s^2+4)(s^2+2s+2)}\}\\=\mathcal L^{-1}\{10\sin 2\cdot { se^{-s} \over (s^2+4)(s^2+2s+2)}+ 20\cos 2\cdot {e^{-s}\over (s^2+4)(s^2+2s+2)}\} \\=-\sin 2\cdot u(t-1)(\cos(2t-2)-2\sin(2t-2)-e^{1-t}(\cos(t-1)-3\sin(t-1)))\\ \quad -\cos 2\cdot u(t-1)(2\cos(2t-2)+ \sin(2t-2)-2e^{1-t}(\cos(t-1)+2\sin(t-1))))\\ 因此\mathcal L^{-1}\{Y(s)\} = \bbox[red,2pt]{y(t)=-2 \cos(2t)-\sin(2t)+ 3e^{-t}\cos t +u(t-1)(\sin(2t)+2\cos(2t))\\ -u(t-1)\sin 2\cdot e^{1-t}(\cos(t-1)-3\sin(t-1))-2u(t-1)\cos 2\cdot e^{1-t}(\cos(t-1)+2\sin(t-1))}$$解答:$$\mathbf{(一)}\begin{bmatrix}0 & 0 & -2 & 1 & 0 & 0\\1 & 2 & 1 & 0 & 1 & 0\\1 & 0 &3 & 0 & 0 &1 \end{bmatrix} \xrightarrow{R_3+R_1,-R_3+R_2} \begin{bmatrix}1 & 0 & 1 & 1 & 0 & 1\\0 & 2 & -2 & 0 & 1 & -1\\1 & 0 &3 & 0 & 0 &1 \end{bmatrix} \\ \xrightarrow{-R_1+R_3,R_2/2} \begin{bmatrix}1 & 0 & 1 & 1 & 0 & 1\\0 & 1 & -1 & 0 & 1/2 & -1/2\\0 & 0 &2 & -1 & 0 &0 \end{bmatrix} \xrightarrow{R_3/2+R_2,R_3/2} \begin{bmatrix}1 & 0 & 1 & 1 & 0 & 1\\0 & 1 & 0 &-1/2 & 1/2 & -1/2\\0 & 0 &1 & -1/2 & 0 &0 \end{bmatrix} \\ \xrightarrow{-R_3 +R_1} \begin{bmatrix}1 & 0 & 0 & 3/2 & 0 & 1\\0 & 1 & 0 &-1/2 & 1/2 & -1/2\\0 & 0 &1 & -1/2 & 0 &0 \end{bmatrix} \Rightarrow \bbox[red, 2pt]{A^{-1}= \begin{bmatrix}3/2 &0 &1 \\-1/2 & 1/2 & -1/2 \\-1/2 & 0 & 0\end{bmatrix}}\\ \mathbf{(二)}\det(A-\lambda I)=0 \Rightarrow \lambda^3+5\lambda^2 -8\lambda+ 4= -(\lambda-1)(\lambda-2)^2= 0 \\ \Rightarrow \bbox[red, 2pt]{特徵值=1,2} \\\mathbf{(三)}計算特徵值對應的特徵向量\\ \lambda_1=1 \Rightarrow (A-\lambda_1 I)=0 \Rightarrow \begin{bmatrix}-1 & 0 & -2\\ 1& 1& 1\\ 1& 0 &2 \end{bmatrix}\begin{bmatrix}x_1\\ x_2\\ x_3 \end{bmatrix}=0 \Rightarrow \cases{x_1+2x_3=0\\ x_2=x_3},取v_1=\begin{bmatrix}-2\\ 1\\ 1 \end{bmatrix}\\ \lambda_2=2 \Rightarrow (A-\lambda_2 I)=0 \Rightarrow \begin{bmatrix}2 & 0 & -2\\ 1& 0& 1\\ 1& 0 &1 \end{bmatrix}\begin{bmatrix}x_1\\ x_2\\ x_3 \end{bmatrix}=0 \Rightarrow x_1=-x_3,取v_2=\begin{bmatrix}0\\ 1\\ 0 \end{bmatrix},v_3=\begin{bmatrix}-1\\ 0\\ 1 \end{bmatrix}\\ \Rightarrow P=[v_1\;v_2\;v_3] =\begin{bmatrix}-2 & 0 & -1\\ 1& 1& 0\\ 1& 0 &1 \end{bmatrix} \Rightarrow P^{-1}=\begin{bmatrix}-1 & 0 & -1\\ 1& 1& 1\\ 1& 0 &2 \end{bmatrix} \Rightarrow A=P\begin{bmatrix}\lambda_1 & 0 & 0\\ 0& \lambda_2& 0\\ 0& 0 &\lambda_2 \end{bmatrix}P^{-1} \\ \Rightarrow \bbox[red, 2pt]{P=\begin{bmatrix}-2 & 0 & -1\\ 1& 1& 0\\ 1& 0 &1 \end{bmatrix},D=\begin{bmatrix}1 & 0 & 0\\ 0 & 2 & 0\\ 0 & 0 & 2 \end{bmatrix}} \\\mathbf{(四)}A^{13}=PD^{13}P= \begin{bmatrix}-2 & 0 & -1\\ 1& 1& 0\\ 1& 0 &1 \end{bmatrix} \begin{bmatrix}1 & 0 & 0\\ 0 & 2^{13} & 0\\ 0 & 0 & 2^{13} \end{bmatrix} \begin{bmatrix}-1 & 0 & -1\\ 1& 1& 1\\ 1& 0 &2 \end{bmatrix}\\ = \bbox[red, 2pt]{\left[\begin{matrix}-8190 & 0 & -16382 \\8191 & 8192 & 8191 \\8191 & 0 & 16383 \end{matrix}\right]}$$
乙、測驗題部分:(50 分)
解答:$$(A) \bigcirc: 不平行的兩平面相交為一直線,有無限多組解\\ (B)\bigcirc: (2,1,0)均在兩平面上 \\ (C)\bigcirc: (-1,3,1)均在兩平面上 \\ (D)\times:直線的維度為1\\故選\bbox[red, 2pt]{(D)}$$解答:$$M=\left[\begin{matrix}-1 & 1 & -1 & 0\\0 & 1 & 0 & 0\\1 & 0 & 1 & 0\\0 & 0 & -1 & -1\end{matrix}\right] \Rightarrow rref(M)= \left[\begin{matrix}1 & 0 & 0 & -1\\0 & 1 & 0 & 0\\0 & 0 & 1 & 1\\0 & 0 & 0 & 0\end{matrix}\right] \Rightarrow rank(M)=3,故選\bbox[red, 2pt]{(C)}$$
解答:$$令X=\begin{bmatrix} 1\\ 1\end{bmatrix} \Rightarrow AX =\begin{bmatrix} 5 \\ 11 \end{bmatrix}, 不存在\lambda 滿足AX=\lambda X, 故選\bbox[red, 2pt]{(D)}$$
解答:$$T(x,y,z)=0 \Rightarrow \cases{2x=0\\ y-z=0} \Rightarrow \cases{x=0\\ y=z} \Rightarrow ker(T)=\{(0,a,a)\mid a\in \mathbb R\} 為一直線 \\ \Rightarrow 維度=1,故選\bbox[red, 2pt]{(A)}$$
解答:$$S=\{(a,0,0,b)\mid a,b\in \mathbb R\} \Rightarrow d(S,u) =\sqrt{(a-1)^2+1^2+3^2 +(b-5)^2}\\ 當a=1,b=5時,d(S,u)有最小值\sqrt{1+9}=\sqrt{10},故選\bbox[red, 2pt]{(B)}$$
解答:$$A,B相似\Rightarrow \det(B)=\det(A)=3 \Rightarrow \det(AB)=\det(A)\det(B)=9,故選\bbox[red, 2pt]{(D)}$$
解答:$$假設特徵值\cases{\lambda_1=-3\\ \lambda_2=1\\ \lambda_3=2}相對應的特徵向量為\cases{v_1\\ v_2\\ v_3}\\ 則(A^2+3A+2I)v_i= A^2v_i+ 3Av_i+2Iv_i =\lambda_i^2v_i +3\lambda_iv_i +2v_i =(\lambda_i^2 +3\lambda_i+2)v_i\\ \Rightarrow A^2+3A+2I的特徵值為\lambda_i^2 +3\lambda_i+2, 分別是\cases{9-9+2=2\\ 1+3+2=6\\ 4+6+2=12} \\ \Rightarrow \det(A^2+3A+2I) =2\times 6\times 12=144,故選\bbox[red, 2pt]{(A)}$$
解答:$$A=\begin{bmatrix}0.8 & 0.3\\ 0.2 & 0.7 \end{bmatrix} =\begin{bmatrix} -1 & 1.5 \\ 1 & 1 \end{bmatrix}\begin{bmatrix} 0.5 & 0 \\ 0 & 1\end{bmatrix}\begin{bmatrix} -0.4 & 0.6\\ 0.4& 0.4\end{bmatrix} \\ \Rightarrow A^{\infty} =\begin{bmatrix} -1 & 1.5 \\ 1 & 1 \end{bmatrix}\begin{bmatrix} 0 & 0 \\ 0 & 1\end{bmatrix}\begin{bmatrix} -0.4 & 0.6\\ 0.4& 0.4\end{bmatrix} =\begin{bmatrix} 0.6 & 0.6\\ 0.4 & 0.4 \end{bmatrix},故選\bbox[red, 2pt]{(B)}$$
解答:$$(A)\times: \cos(z)={1\over 2}(e^{iz}+e^{-iz}) \Rightarrow {d\over dz}\cos(z) ={1\over 2}(ie^{iz}-ie^{-iz}) =-{1\over 2i}(e^{iz}-e^{-iz}) =-\sin(z) \\ (B)\bigcirc: \cos(z) = \cos(x+iy) = \cos x\cos(iy) − \sin x\sin(iy) = \cos x\cosh y − i\sin x\sinh y \\ \qquad \Rightarrow \cases{u=\cos x\cosh y\\ v=-\sin x \sinh y} \Rightarrow \cases{{\partial v\over \partial x}=- \cos x\sinh y\\ {\partial u\over \partial y}=\cos x\sinh y} \Rightarrow {\partial v\over \partial x}=-{\partial u\over \partial y} \\(C)\times: u(x,y)=\cos x\cosh y=\cos x\cdot {e^y+e^{-y}\over 2 }\\(D)\times: v(x,y)=-\sin x\sinh y =-\sin x{e^y-e^{-y}\over 2}\\,故選\bbox[red, 2pt]{(B)}$$
解答:$$e^{2z+\ln(2)} =1+i =\sqrt 2(\cos{\pi\over 4}+i\sin{\pi\over 4}) =\sqrt 2e^{\pi i/4} =e^{{1\over 2}\ln(2)+{\pi\over 4}i} \\ \Rightarrow 2z+\ln(2) ={1\over 2}\ln(2)+{\pi\over 4}i \Rightarrow z=-{1\over 4}\ln(2)+{\pi \over 8}i,故選\bbox[red, 2pt]{(C)}$$
解答:$$z=t-it^2 \Rightarrow dz=dt-2itdt= (1-2it)dt \Rightarrow \int_C (1-z)dz =\int_0^1 (1-t+it^2)(1-2it)dt \\= \int_0^1 2t^3+3it^2-(2i+1)t+1 \,dt = \left. \left[ {1\over 2}t^4 +it^3-(i+{1\over 2})t^2+ t\right]\right|_0^1 \\={1\over 2}+i-(i+{1\over 2})+1=1,故選\bbox[red, 2pt]{(B)}$$
解答:$$z^2+i6z=z(z+6i)=0 \Rightarrow z=0,-6i; 由於0及-6i皆在路徑外,故選\bbox[red, 2pt]{(A)}$$
解答:$$若未給定初始值,有無窮多解,故選\bbox[red, 2pt]{(A)}$$
解答:$$\cases{u(x,y)={2y\over x}-9\\ v(x,y)= 3-{6x\over y}} \Rightarrow \cases{x^2y^2 u(x,y)=2xy^3-9x^2y^2 \\ x^2y^2v(x,y)= 3x^2y^2-6x^3y} \\ \Rightarrow \cases{{\partial \over \partial y}x^2y^2 u(x,y) =6xy^2-18x^2y \\{\partial \over \partial x}x^2y^2v(x,y) =6xy^2-18x^2y} \Rightarrow {\partial \over \partial y}x^2y^2 u(x,y)={\partial \over \partial x}x^2y^2v(x,y)\\ \Rightarrow x^2y^2 為積分因子,故選\bbox[red, 2pt]{(D)}$$
解答:$$y=a_0+ a_1x+a_2x^2 +\cdots+a_nx^n+\cdots\\ \Rightarrow \cases{xy= a_0x+ a_1x^2+ a_2x^3+\cdots + a_nx^{n+1}+ \cdots\\ y'=a_1 +2a_2x + \cdots +na_nx^{n-1}+ \cdots} \\ \Rightarrow y'+xy = a_1+(a_0+2x_2)x +\cdots +(a_{n-1}+ (n+1)a_{n+1})x^n+\cdots =0\\ \Rightarrow a_{n-1}+ (n+1)a_{n+1}=0 \Rightarrow a_{n+1}=-{1\over n+1}a_{n-1},故選\bbox[red, 2pt]{(C)}$$
解答:$$g(t)=\begin{cases}0, & t\lt 5\\ t-5, &t\ge 5 \end{cases} \Rightarrow \mathcal L\{ g(t)\} =\int_5^\infty (t-5)e^{-st}\,dt =\left. \left[-{e^{-st} \over s^2}(s(t-5)+1) \right] \right|_5^\infty \\ =0+{e^{-5t}\over s^2}={e^{-5t}\over s^2},故選\bbox[red, 2pt]{(B)}$$
解答:$$(A)\times: f為偶函數 \Rightarrow b_n=0\\ (B)\times: f為奇函數\Rightarrow a_n=0\\ (C)\times: A={n\pi \over L} \ne {2n\pi \over L} \\ (D)\bigcirc: f為奇函數\Rightarrow a_n=0 \Rightarrow f(x)= \sum_{n=1}^\infty b_n \sin{n\pi\over L}x \\ \qquad \Rightarrow \lim_{x\to L^-}f(x) =\lim_{x\to L^-}\sum_{n=1}^\infty b_n \sin{n\pi\over L}x =\sum_{n=1}^\infty b_n\lim_{x\to L^-} \left( \sin{n\pi\over L}x\right) =0\\,故選\bbox[red, 2pt]{(D)}$$
解答:$${沒肺癌且不抽菸\over 沒肺癌且抽菸+沒肺癌且不抽菸} ={70\% \times 90\% \over 30\%\times 60\%+ 70\% \times 90\%} \\ ={63\over 18+63}={7\over 9},故選\bbox[red, 2pt]{(A)}$$
解答:$$P(2\le X\le 4)=0.4 \Rightarrow {4-2\over A}=0.4 \Rightarrow A=2\times {10\over 4}=5,故選\bbox[red, 2pt]{(C)}$$
解答:$$Y=-4X+1 \Rightarrow Var(Y)=Var(-4X+1)= 16Var(X)=16\\ 又4X+Y=1 \Rightarrow Var(4X+Y)=Var(1)=0 \Rightarrow 16Var(X)+Var(Y)+8Cov(X,Y)=0\\ \Rightarrow 32+8Cov(X,Y)=0 \Rightarrow Cov(X,Y)=-4,故選\bbox[red, 2pt]{(D)}$$
解答:$$S=\{(a,0,0,b)\mid a,b\in \mathbb R\} \Rightarrow d(S,u) =\sqrt{(a-1)^2+1^2+3^2 +(b-5)^2}\\ 當a=1,b=5時,d(S,u)有最小值\sqrt{1+9}=\sqrt{10},故選\bbox[red, 2pt]{(B)}$$
解答:$$A,B相似\Rightarrow \det(B)=\det(A)=3 \Rightarrow \det(AB)=\det(A)\det(B)=9,故選\bbox[red, 2pt]{(D)}$$
解答:$$假設特徵值\cases{\lambda_1=-3\\ \lambda_2=1\\ \lambda_3=2}相對應的特徵向量為\cases{v_1\\ v_2\\ v_3}\\ 則(A^2+3A+2I)v_i= A^2v_i+ 3Av_i+2Iv_i =\lambda_i^2v_i +3\lambda_iv_i +2v_i =(\lambda_i^2 +3\lambda_i+2)v_i\\ \Rightarrow A^2+3A+2I的特徵值為\lambda_i^2 +3\lambda_i+2, 分別是\cases{9-9+2=2\\ 1+3+2=6\\ 4+6+2=12} \\ \Rightarrow \det(A^2+3A+2I) =2\times 6\times 12=144,故選\bbox[red, 2pt]{(A)}$$
解答:$$A=\begin{bmatrix}0.8 & 0.3\\ 0.2 & 0.7 \end{bmatrix} =\begin{bmatrix} -1 & 1.5 \\ 1 & 1 \end{bmatrix}\begin{bmatrix} 0.5 & 0 \\ 0 & 1\end{bmatrix}\begin{bmatrix} -0.4 & 0.6\\ 0.4& 0.4\end{bmatrix} \\ \Rightarrow A^{\infty} =\begin{bmatrix} -1 & 1.5 \\ 1 & 1 \end{bmatrix}\begin{bmatrix} 0 & 0 \\ 0 & 1\end{bmatrix}\begin{bmatrix} -0.4 & 0.6\\ 0.4& 0.4\end{bmatrix} =\begin{bmatrix} 0.6 & 0.6\\ 0.4 & 0.4 \end{bmatrix},故選\bbox[red, 2pt]{(B)}$$
解答:$$(A)\times: \cos(z)={1\over 2}(e^{iz}+e^{-iz}) \Rightarrow {d\over dz}\cos(z) ={1\over 2}(ie^{iz}-ie^{-iz}) =-{1\over 2i}(e^{iz}-e^{-iz}) =-\sin(z) \\ (B)\bigcirc: \cos(z) = \cos(x+iy) = \cos x\cos(iy) − \sin x\sin(iy) = \cos x\cosh y − i\sin x\sinh y \\ \qquad \Rightarrow \cases{u=\cos x\cosh y\\ v=-\sin x \sinh y} \Rightarrow \cases{{\partial v\over \partial x}=- \cos x\sinh y\\ {\partial u\over \partial y}=\cos x\sinh y} \Rightarrow {\partial v\over \partial x}=-{\partial u\over \partial y} \\(C)\times: u(x,y)=\cos x\cosh y=\cos x\cdot {e^y+e^{-y}\over 2 }\\(D)\times: v(x,y)=-\sin x\sinh y =-\sin x{e^y-e^{-y}\over 2}\\,故選\bbox[red, 2pt]{(B)}$$
解答:$$e^{2z+\ln(2)} =1+i =\sqrt 2(\cos{\pi\over 4}+i\sin{\pi\over 4}) =\sqrt 2e^{\pi i/4} =e^{{1\over 2}\ln(2)+{\pi\over 4}i} \\ \Rightarrow 2z+\ln(2) ={1\over 2}\ln(2)+{\pi\over 4}i \Rightarrow z=-{1\over 4}\ln(2)+{\pi \over 8}i,故選\bbox[red, 2pt]{(C)}$$
解答:$$z=t-it^2 \Rightarrow dz=dt-2itdt= (1-2it)dt \Rightarrow \int_C (1-z)dz =\int_0^1 (1-t+it^2)(1-2it)dt \\= \int_0^1 2t^3+3it^2-(2i+1)t+1 \,dt = \left. \left[ {1\over 2}t^4 +it^3-(i+{1\over 2})t^2+ t\right]\right|_0^1 \\={1\over 2}+i-(i+{1\over 2})+1=1,故選\bbox[red, 2pt]{(B)}$$
解答:$$z^2+i6z=z(z+6i)=0 \Rightarrow z=0,-6i; 由於0及-6i皆在路徑外,故選\bbox[red, 2pt]{(A)}$$
解答:$$若未給定初始值,有無窮多解,故選\bbox[red, 2pt]{(A)}$$
解答:$$\cases{u(x,y)={2y\over x}-9\\ v(x,y)= 3-{6x\over y}} \Rightarrow \cases{x^2y^2 u(x,y)=2xy^3-9x^2y^2 \\ x^2y^2v(x,y)= 3x^2y^2-6x^3y} \\ \Rightarrow \cases{{\partial \over \partial y}x^2y^2 u(x,y) =6xy^2-18x^2y \\{\partial \over \partial x}x^2y^2v(x,y) =6xy^2-18x^2y} \Rightarrow {\partial \over \partial y}x^2y^2 u(x,y)={\partial \over \partial x}x^2y^2v(x,y)\\ \Rightarrow x^2y^2 為積分因子,故選\bbox[red, 2pt]{(D)}$$
解答:$$y=a_0+ a_1x+a_2x^2 +\cdots+a_nx^n+\cdots\\ \Rightarrow \cases{xy= a_0x+ a_1x^2+ a_2x^3+\cdots + a_nx^{n+1}+ \cdots\\ y'=a_1 +2a_2x + \cdots +na_nx^{n-1}+ \cdots} \\ \Rightarrow y'+xy = a_1+(a_0+2x_2)x +\cdots +(a_{n-1}+ (n+1)a_{n+1})x^n+\cdots =0\\ \Rightarrow a_{n-1}+ (n+1)a_{n+1}=0 \Rightarrow a_{n+1}=-{1\over n+1}a_{n-1},故選\bbox[red, 2pt]{(C)}$$
解答:$$g(t)=\begin{cases}0, & t\lt 5\\ t-5, &t\ge 5 \end{cases} \Rightarrow \mathcal L\{ g(t)\} =\int_5^\infty (t-5)e^{-st}\,dt =\left. \left[-{e^{-st} \over s^2}(s(t-5)+1) \right] \right|_5^\infty \\ =0+{e^{-5t}\over s^2}={e^{-5t}\over s^2},故選\bbox[red, 2pt]{(B)}$$
解答:$$(A)\times: f為偶函數 \Rightarrow b_n=0\\ (B)\times: f為奇函數\Rightarrow a_n=0\\ (C)\times: A={n\pi \over L} \ne {2n\pi \over L} \\ (D)\bigcirc: f為奇函數\Rightarrow a_n=0 \Rightarrow f(x)= \sum_{n=1}^\infty b_n \sin{n\pi\over L}x \\ \qquad \Rightarrow \lim_{x\to L^-}f(x) =\lim_{x\to L^-}\sum_{n=1}^\infty b_n \sin{n\pi\over L}x =\sum_{n=1}^\infty b_n\lim_{x\to L^-} \left( \sin{n\pi\over L}x\right) =0\\,故選\bbox[red, 2pt]{(D)}$$
解答:$${沒肺癌且不抽菸\over 沒肺癌且抽菸+沒肺癌且不抽菸} ={70\% \times 90\% \over 30\%\times 60\%+ 70\% \times 90\%} \\ ={63\over 18+63}={7\over 9},故選\bbox[red, 2pt]{(A)}$$
解答:$$P(2\le X\le 4)=0.4 \Rightarrow {4-2\over A}=0.4 \Rightarrow A=2\times {10\over 4}=5,故選\bbox[red, 2pt]{(C)}$$
解答:$$Y=-4X+1 \Rightarrow Var(Y)=Var(-4X+1)= 16Var(X)=16\\ 又4X+Y=1 \Rightarrow Var(4X+Y)=Var(1)=0 \Rightarrow 16Var(X)+Var(Y)+8Cov(X,Y)=0\\ \Rightarrow 32+8Cov(X,Y)=0 \Rightarrow Cov(X,Y)=-4,故選\bbox[red, 2pt]{(D)}$$
================== END =====================





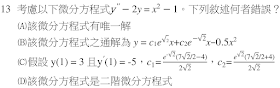

沒有留言:
張貼留言