國立臺北大學110學年度碩士班一般入學考試
系(所)組別:通訊工程系
科目:工程數學(線性代數與機率)
解答:$$\left[\begin{array}{cccc|cccc}1 & 1 & 1 & 1 & 1 & 0 & 0 & 0 \\1 & 2 & 2 & 1 & 0 & 1 & 0 & 0 \\1 & 2 & 3 & 4 & 0 & 0 & 1 & 0 \\3 & 3 & 1 & 1 & 0 & 0 & 0 & 1\end{array}\right] \xrightarrow{-R_1+R_2\to R_2,-R_1+R_3\to R_3,-3R_1+R_3\to R_3}\\ \left[\begin{array}{cccc|cccc}1 & 1 & 1 & 1 & 1 & 0 & 0 & 0 \\0 & 1 & 1 & 0 & -1 & 1 & 0 & 0 \\0 & 1 & 2 & 3 & -1 & 0 & 1 & 0 \\0 & 0 & -2 & -2 & -3 & 0 & 0 & 1\end{array}\right] \xrightarrow{-R_2+R_3\to R_3, R_4/-2} \left[\begin{array}{cccc|cccc}1 & 1 & 1 & 1 & 1 & 0 & 0 & 0 \\0 & 1 & 1 & 0 & -1 & 1 & 0 & 0 \\0 & 0 & 1 & 3 & 0 & -1 & 1 & 0 \\0 & 0 & 1 & 1 & 3/2 & 0 & 0 & -1/2 \end{array}\right]\\ \xrightarrow{-R_2+R_1\to R_1,-R_3+R_4\to R_4} \left[\begin{array}{cccc|cccc}1 & 0 & 0 & 1 & 2 & -1 & 0 & 0 \\0 & 1 & 1 & 0 & -1 & 1 & 0 & 0 \\0 & 0 & 1 & 3 & 0 & -1 & 1 & 0 \\0 & 0 & 0 & -2 & 3/2 & 1 & -1 & -1/2 \end{array}\right] \xrightarrow{-R_3+R_2 \to R_2, R_4/2}\\ \left[\begin{array}{cccc|cccc}1 & 0 & 0 & 1 & 2 & -1 & 0 & 0 \\0 & 1 & 0 & -3 & -1 & 2 & -1 & 0 \\0 & 0 & 1 & 3 & 0 & -1 & 1 & 0 \\0 & 0 & 0 & 1 & -3/4 & -1/2 & 1/2 & 1/4 \end{array}\right] \xrightarrow{3R_4+R_2\to R_2,-3R_4+R_3\to R_3} \\\left[\begin{array}{cccc|cccc}1 & 0 & 0 & 1 & 2 & -1 & 0 & 0 \\0 & 1 & 0 & 0 & -13/4 & 1/2 & 1/2 & 3/4 \\0 & 0 & 1 & 0 & 9/4 & 1/2 & -1/2 & -3/4 \\0 & 0 & 0 & 1 & -3/4 & -1/2 & 1/2 & 1/4 \end{array}\right] \xrightarrow{-R_4+R_1\to R_1} \\ \left[\begin{array}{cccc|cccc}1 & 0 & 0 & 0 & 11/4 & -1/2 & -1/2 & -1/4 \\0 & 1 & 0 & 0 & -13/4 & 1/2 & 1/2 & 3/4 \\0 & 0 & 1 & 0 & 9/4 & 1/2 & -1/2 & -3/4 \\0 & 0 & 0 & 1 & -3/4 & -1/2 & 1/2 & 1/4 \end{array}\right] \Rightarrow A^{-1}= \bbox[red, 2pt]{\left[\begin{array}{ } 11/4 & -1/2 & -1/2 & -1/4 \\ -13/4 & 1/2 & 1/2 & 3/4 \\ 9/4 & 1/2 & -1/2 & -3/4 \\ -3/4 & -1/2 & 1/2 & 1/4 \end{array}\right] }$$解答:$$A=\begin{bmatrix}2 & 3\\4 & 1\end{bmatrix} =\begin{bmatrix}{1\over \sqrt 2} & {-3\over 5} \\{1\over \sqrt 2} & {4\over 5} \end{bmatrix} \begin{bmatrix}5 & 0\\0 & -2\end{bmatrix} \begin{bmatrix}{1\over \sqrt 2} & {-3\over 5} \\{1\over \sqrt 2} & {4\over 5} \end{bmatrix}^{-1} \\ \Rightarrow A^{4}=\begin{bmatrix}{1\over \sqrt 2} & {-3\over 5} \\{1\over \sqrt 2} & {4\over 5} \end{bmatrix} \begin{bmatrix}5^4 & 0\\0 & (-2)^{4} \end{bmatrix} \begin{bmatrix}{1\over \sqrt 2} & {-3\over 5} \\{1\over \sqrt 2} & {4\over 5} \end{bmatrix}^{-1} =\begin{bmatrix}{625\over \sqrt 2} & {-48\over 5} \\{625\over \sqrt 2} & {64\over 5} \end{bmatrix}\begin{bmatrix}{1\over \sqrt 2} & {-3\over 5} \\{1\over \sqrt 2} & {4\over 5} \end{bmatrix}^{-1} \\=\begin{bmatrix}{625\over \sqrt 2} & {-48\over 5} \\{625\over \sqrt 2} & {64\over 5} \end{bmatrix}\begin{bmatrix}{4\sqrt 2\over 7} & {3\sqrt 2\over 7} \\{-5\over 7} & {5\over 7} \end{bmatrix} =\begin{bmatrix} 364
&261 \\348 &277 \end{bmatrix}\\ 因此\begin{bmatrix}0.4 & 0.6 \\0.8 & 0.2\end{bmatrix}^4 =({1\over 5}A)^4={1 \over 625}A^4={1\over 625}\begin{bmatrix} 364 &261 \\348 &277 \end{bmatrix} =\bbox[red, 2pt]{\begin{bmatrix} {364\over 625} & {261\over 625} \\ {348\over 625} & {277\over 625} \end{bmatrix}}$$
解答:$$\det(A)=4a^2-10a = 2a(2a-5)=0 \Rightarrow \bbox[red, 2pt]{a=0,{5\over 2}}$$
解答:$$令\cases{\mathbf a_1=(1,2,0,0)\\\mathbf a_2= (1,-3,0,0)\\\mathbf a_3=(-1,3,1 ,3)\\\mathbf a_4= (1,-3,2,-4) } \Rightarrow \mathbf u_1=\mathbf a_1=(1,2,0,0) \Rightarrow \mathbf e_1={\mathbf u_1\over |\mathbf u_1|} =({1\over \sqrt 5}, {2\over \sqrt 5},0,0)\\ \mathbf u_2= \mathbf a_2-(\mathbf a_2\cdot \mathbf e_1)\mathbf e_1 =(1,-3,0,0)+\sqrt 5({1\over \sqrt 5}, {2\over \sqrt 5},0,0) =(2,-1,0,0)\\ \Rightarrow \mathbf e_2={\mathbf u_2\over |\mathbf u_2|} =({2\over \sqrt 5},-{1 \over \sqrt 5},0,0) \\ \mathbf u_3= \mathbf a_3-(\mathbf a_3 \cdot \mathbf e_1)\mathbf e_1- (\mathbf a_3 \cdot \mathbf e_2)e_2= (-1,3,1,3)-\sqrt 5({1\over \sqrt 5}, {2\over \sqrt 5},0,0) +\sqrt 5({2\over \sqrt 5},-{1 \over \sqrt 5},0,0) \\=(0,0,1,3) \Rightarrow \mathbf e_3={\mathbf u_3\over |\mathbf u_3|} =(0,0,{1\over \sqrt{10}}, {3\over \sqrt{10}}) \\ \mathbf u_4=\mathbf a_4-(\mathbf a_4\cdot \mathbf e_1)\mathbf e_1- (\mathbf a_4\cdot \mathbf e_2)\mathbf e_2- (\mathbf a_4\cdot \mathbf e_3)\mathbf e_3\\ =(1,-3,2,-4)+\sqrt 5({1\over \sqrt 5}, {2\over \sqrt 5},0,0)-\sqrt 5({2\over \sqrt 5},-{1 \over \sqrt 5},0,0)+ \sqrt{10}(0,0,{1\over \sqrt{10}}, {3\over \sqrt{10}}) \\=(0,0,3,-1) \Rightarrow \mathbf e_4= { \mathbf u_4\over |\mathbf u_4|} =(0,0,{3\over \sqrt{10}},{-1\over \sqrt{10}}) \\ 因此Q=[\mathbf e_1 | \mathbf e_2 | \mathbf e_3| \mathbf e_4] \Rightarrow \bbox[red, 2pt]{Q=\begin{bmatrix}1/\sqrt 5 & 2/\sqrt 5 & 0 & 0 \\2/\sqrt 5 & -1/\sqrt 5& 0 & 0\\ 0 & 0 & 1/\sqrt{10} & 3/\sqrt{10} \\ 0 & 0 & 3/\sqrt{10} & -1/\sqrt{10} \end{bmatrix}}\\ \Rightarrow R=\begin{bmatrix}\mathbf a_1\cdot \mathbf e_1 & \mathbf a_2\cdot \mathbf e_1 & \mathbf a_3\cdot \mathbf e_1 & \mathbf a_4\cdot \mathbf e_1\\0 & \mathbf a_2\cdot \mathbf e_2 & \mathbf a_3\cdot \mathbf e_2 & \mathbf a_4 \cdot \mathbf e_2 \\ 0 & 0 & \mathbf a_3\cdot \mathbf e_3 & \mathbf a_4\cdot \mathbf e_3\\ 0 & 0 & 0 & \mathbf a_4\cdot \mathbf e_4\end{bmatrix}\Rightarrow \bbox[red, 2pt]{R= \begin{bmatrix}\sqrt 5 & -\sqrt 5& \sqrt 5& -\sqrt 5 \\0 & \sqrt 5& -\sqrt 5& \sqrt 5\\ 0 & 0 &\sqrt{10} &-\sqrt{10}\\ 0 & 0 & 0 &\sqrt{10} \end{bmatrix}}$$
解答:$$\cases{\det(AB)=\det(A)\det(B) \\ \det(A^T)=\det(A)} \Rightarrow \det(AB) =\left|\begin{matrix}0 & 0 & 3 & -4 \\2 & -3 & 3 & -3 \\0 & 0 & 1 & 2 \\1 & 1 & -1 & 1
\end{matrix} \right| \left|\begin{matrix}1 & 2 & -1 & 2 \\-3 & 4 & 3 & -6 \\0 & 0 & 1 & 4 \\0 & 0 & 3 & -8\end{matrix}\right| \\=-50\times (-200)=\bbox[red, 2pt]{10000}$$
解答:$$\mathbf{(a)}\;f_X(x)=\int_0^\infty 10e^{-(5x+2y)}\,dy =\left. \left[ -5e^{-(5x+2y)}\right] \right|_0^\infty = 5e^{-5x} \\ \quad \Rightarrow \bbox[red, 2pt]{f_X(x)=5e^{-5x},x\ge 0} \\ \mathbf{(b)}E(X)=\int_0^\infty 5xe^{-5x}\,dx =\left. \left[-{1\over 5}e^{-5x}(5x+1) \right] \right|_0^\infty=\bbox[red, 2pt]{1\over 5} \\\mathbf{(c)}\;f_Y(y)= \int_0^\infty 10e^{-(5x+2y)}\,dx=2e^{-2y} \Rightarrow F_Y(x)=\int_0^x 2e^{-2y}\,dy=1-e^{-2x}\\ 同理,F_X(x)=\int_0^x 5e^{-5x}\,dx = 1-e^{-5x}\\ 因此\text{CDF of }\min(X,Y) =P(\min(X,Y)\le z) =F_X(z)+F_Y(z)-F_X(z)F_Y(z)\\ =(1-e^{-5z})+(1-e^{-2z})-(1-e^{-5z}) (1-e^{-2z}) =1-e^{-7z}\\ \Rightarrow \text{CDF of }\min(X,Y) =\bbox[red, 2pt]{1-e^{-7z},z=\min(X,Y)}$$
解答:$$\mathbf{(a)}\;P_X(x=1)+ P_X(x=2)+ P_X(x=3)=1 \Rightarrow c+{c\over 2}+{c\over 3}={11c\over 6}=1 \Rightarrow c= \bbox[red, 2pt]{6\over 11} \\ \mathbf{(b)}\; P[2\le X\le 8]=P(X=2)+ P(X=3) ={c\over 2}+{c\over 3} ={5c\over 6} ={5\over 6}\cdot {6\over 11}= \bbox[red, 2pt]{5\over 11} \\ \mathbf{(c)}\; EX^2= 1^2P(x=1)+ 2^2P(X=2)+ 3^2P(X=3)=1\cdot {c\over 1}+ 4\cdot {c\over 2}+ 9\cdot {c\over 3}=6c= \bbox[red, 2pt]{36\over 11}$$
解答:$$\mathbf{(a)}\; \mathbf{No}: \cases{E_1 \text{ and }E_2\text{ are disjoint } \Rightarrow P(E_1\cap E_2) =P(\varnothing)=0 \\ E_1 \text{ and }E_2\text{ are independent } \Rightarrow P(E_1\cap E_2) =P(E_1)P(E_2)},兩者不一定相等\\ \mathbf{(b)}\;\mathbf{No}: P(E_1\cup E_2)= P(E_1) +P(E_2)-P(E_1\cap E_2) \\\mathbf{(c)}\; \mathbf{No}: 連續型機率密度函數沒有單點機率值\\ \mathbf{(d)}\; \mathbf{No}: \int_0^\infty e^{-2x}\,dx = {1\over 2}\ne 1$$
==================== END =======================
解題僅供參考

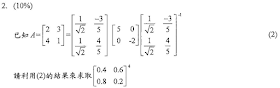






沒有留言:
張貼留言