臺北市113 學年度市立國民中學正式教師聯合甄選
貳、專業科目
選擇題(共 40 題,每題 1.75 分,共 70 分)
解答:$$\cases{7-\sqrt{x+1} \ge 7 \Rightarrow a=7\\ x^2+6x-3=(x+3)^2-12 \Rightarrow b=-12} \Rightarrow ab=7\cdot (-12)=-84,故選\bbox[red, 2pt]{(B)}$$
解答:$$a:b:c=1: 2: 3 \Rightarrow \cases{a=k\\ b=2k\\ c=3k}\\ \Rightarrow f(a+b+c)= {(b+c)(a+c)(a+b)\over abc} +{ab+bc+ca\over (a+b+c)^2} \\\qquad ={5k\cdot 4k\cdot 3k \over 6k^3} +{2k^2+6k^2+ 3k^2 \over (6k)^2} =10+{11\over 36}={371\over 36},故選\bbox[red, 2pt]{(A)}$$
解答:$$y=2x^2+5 \xrightarrow{右移一單位} y=2(x-1)^2+5 \xrightarrow{下移2單位} y=2(x-1)^2+5-2\\ \Rightarrow y=2(x-1)^2+3,故選\bbox[red, 2pt]{(D)}$$
解答:$$\cases{甲=6^2 =36\\ 乙=4\times 6=24} \Rightarrow 甲-乙=12,故選\bbox[red, 2pt]{(B)}$$
解答:$$\cases{甲:91球\\ 乙:0球\\ 丙:0球} \xrightarrow{第一步驟}\cases{甲:46球\\ 乙:45球\\ 丙:0球} \xrightarrow{第二步驟}\cases{甲:46球\\ 乙:36球\\ 丙:9球} ,故選\bbox[red, 2pt]{(A)}$$
解答:$$2x+p \lt 4x-2 \Rightarrow 2x \gt p+2 \Rightarrow x\gt {p+2\over 2} \Rightarrow x\gt 1+{p\over 2}\\ (A)\times:p=2 \Rightarrow x\gt 2 \Rightarrow x=3,4,5,\dots,\Rightarrow 小於4的解只有一個 \\(B)\times: p=0 \Rightarrow x\gt 1 \Rightarrow x=2,3,4,\dots,\Rightarrow 小於4的解只有二個 \\(C)\times: p=1 \Rightarrow x\gt {3\over 2}\Rightarrow x=2,3,4,\dots,\Rightarrow 小於4的解只有二個 \\(D)\bigcirc: p=-1 \Rightarrow x\gt {1\over 2} \Rightarrow x=1,2,3,4,\dots,\Rightarrow 小於4的解有三個\\,故選\bbox[red, 2pt]{(D)}$$
解答:$$\sum_{n=1}^{77}[1+(n-1)\times{1\over 4}] =\sum_{n =1}^{77} \left({3\over 4}+{1\over 4}n \right) ={3\over 4}\cdot 77+{1\over 4}\cdot {78\cdot 77\over 2} ={1\over 4}\left(3\cdot 77+39\cdot 77 \right) \\={1\over 4}\cdot 77\cdot 42 ={21\cdot 77\over 2},故選\bbox[red, 2pt]{(C)}$$
解答:$$y=f(x)=ax^2+bx+c \Rightarrow \cases{f(0)=-1\\ f(1)=4\\ f(2)=13} \Rightarrow \cases{c=-1\\ a+b+c=4\\ 4a+2b+c=13} \Rightarrow \cases{a=2\\ b=3\\c=-1} \\ \Rightarrow f(x)=2x^2+3x-1 \Rightarrow f(-1)=2-3-1=-2,故選\bbox[red, 2pt]{(A)}$$
解答:$$\cases{A(5,1)\\ B(-2,3)} \Rightarrow \cases{M=\overline{AB}中點=(3/2,2) \\ \overline{AB}斜率=-2/7} \Rightarrow 中垂線斜率=7/2且經過M\\ \Rightarrow y-2={7\over 2}(x-{3\over 2}) \Rightarrow 14x-4y=13,故選\bbox[red, 2pt]{(D)}$$
解答:$$假設此三整數為a-1,a,a+1 \Rightarrow (a-1)^2+a^2+(a+1)^2=149 \Rightarrow 3a^2+2=149\\ \Rightarrow a^2=49 \Rightarrow a=7 \Rightarrow 三數和=(a-1)+a+(a+1)=3a=21,故選\bbox[red, 2pt]{(B)}$$
解答:$$y=-x^2+4 =0 \Rightarrow x=\pm 2 \Rightarrow \int_{-2}^2( -x^2+4)\,dx =2\int_{0}^2( -x^2+4)\,dx \\=2 \left. \left[ -{1\over 3}x^3+4x \right] \right|_0^2 =2\times {16\over 3}={32\over 3},故選\bbox[red, 2pt]{(A)}$$
解答:$$\begin{array}{c|rrrrr}n & 1& 2& 3& 4 & 5\\\hline 7^n的個位數字& 7 & 9 & 3 & 1& 7\end{array} \Rightarrow 7931循環,循環數為4\\ 7^{2024}=7^{4 \times 506} \Rightarrow 餘1,故選\bbox[red, 2pt]{(C)}$$
解答:$$f(x)=x^7+x^2-1 \Rightarrow f(x=i)=-i-1-1=-i-2=-x-2,故選\bbox[red, 2pt]{(A)}$$
解答:$$x^2+2x+1=(x+1)^2 \ge 0 \Rightarrow {x^3+4x^2-x-4\over x^2+2x+1} \ge 0 \Rightarrow x^3+4x^2-x-4\ge 0 \\ \Rightarrow x^2(x+4)-(x+4)\ge 0 \Rightarrow (x-1)(x+1)(x+4)\ge 0 \Rightarrow x\ge 1 或-4\le x\le -1\\ 但分母不得為0,即x\ne -1,故選\bbox[red, 2pt]{(D)}$$
解答:$$出發前一刻已有7艘輪船在前往巴黎的航線上,因此會遇到2\times 7+1=15艘,故選\bbox[red, 2pt]{(D)}$$
解答:$$\left( x+{1\over x}\right)^{10} =\sum_{n=0}^{10}C^{10}_nx^n\left( {1\over x}\right)^{10-n} \Rightarrow n=6時,係數為C^{10}_6=210,故選\bbox[red, 2pt]{(C)}$$
解答:$$1+{1\over 1+2}+ {1\over 1+2+3}+ \cdots = \sum_{n=1}^\infty{1\over \sum_{k=1}^n k} = \sum_{n=1}^\infty {2\over n(n+1)} =2\sum_{n=1}^\infty \left({1\over n }-{1\over n+1}\right) \\= 2(1-{1\over 2}+{1\over 2}-{1\over 3}+{1\over 3}-{1\over 4}+\cdots )=2,故選\bbox[red, 2pt]{(A)}$$
解答:$$495=11\times 5\times 3^2 \Rightarrow 273x49y5是3的倍數也是11的倍數 \\ \Rightarrow \cases{2+7+3+x+4+9+y+5=30+x+y是3的倍數\\ (2+3+4+y)-(7+x+ 9+5)=y-x-12=0或11的倍數} \\ \Rightarrow \cases{(A)或(D)\\y-x=1,12...} \Rightarrow 其中\cases{x=7\\ y=8}符合要求\Rightarrow x+y=15,故選\bbox[red, 2pt]{(A)}$$
解答:$$\alpha,\beta為x^2-2x-5=0的兩根\Rightarrow \cases{\alpha+ \beta=2\\ \alpha\beta=-5} \Rightarrow \cases{{1\over \alpha}+{1\over \beta}={\alpha+ \beta \over \alpha\beta} =-{2\over 5}\\ {1\over \alpha} \cdot {1\over \beta}= {1\over \alpha\beta} =-{1\over 5}} \\ \Rightarrow x^2+ {2\over 5}x-{1\over 5}=0 \Rightarrow 5x^2+2x-1=0,故選\bbox[red, 2pt]{(C)}$$
解答:$$假設預繳費用的同學有a人,共收了450\times 110\%\times a=495a元\\可支付a+3人費用,即(a+3)\times 450,因此495a=450(a+3) \Rightarrow a=30,故選\bbox[red, 2pt]{(B)}$$
解答:$$L:y=2x-4 \Rightarrow \cases{A(2,0)\\ B(0,-4)\\ P(t,2t-4)} \Rightarrow \triangle OBP面積={1\over 2}\cdot \overline{OB}\cdot |t|=2|t|=8 \Rightarrow |t|=4 \\ \Rightarrow \cases{t=4 \Rightarrow P(4,4)\\ t=-4 \Rightarrow P(-4,-12)} \Rightarrow P的y坐標可能是4,-12,故選\bbox[red, 2pt]{(D)}$$
解答:$$珍珠紅茶熱量=105\times 4+28\times 2.5=490大卡,還剩下1800-490=1310大卡的熱量\\ 又1310=710(肉絲蛋炒飯)+600(燒烤鮭魚飯),熱量最高的是蛋炒飯710大卡,故選\bbox[red, 2pt]{(C)}$$
解答:$$平均數最小,又需滿足中位數為4,由於4=(3+5)\div 2;\\ 又眾數為7,目前已有重複2次的2與3,因此7至少重複3次\\ 因此數列為1,2,2,3,3,5,5,7,7,7\Rightarrow 平均數=4.2,故選\bbox[red, 2pt]{(B)}$$
解答:$$(A)\times: k=22 \Rightarrow \cases{22\le \sqrt a\lt 23\\ 22\le \sqrt{a+50}\lt 23} \Rightarrow \cases{484\le a\lt 529 \Rightarrow 534\le a+50\lt 584\\ 484\le a+50\lt 529}\\ \qquad \Rightarrow 兩區間[534,584),[484,529)無交集 \\(B)\times: k=23 \Rightarrow \cases{23\le \sqrt a\lt 24\\ 23\le \sqrt{a+50}\lt 24} \Rightarrow \cases{529\le a\lt 576 \Rightarrow 579\le a+50\lt 626\\ 529\le a+50\lt 576}\\ \qquad \Rightarrow 兩區間[579,626),[529,576)無交集 \\ (C)\times: k=24 \Rightarrow \cases{24\le \sqrt a\lt 25\\ 24\le \sqrt{a+50}\lt 25} \Rightarrow \cases{576\le a\lt 625 \Rightarrow 626\le a+50\lt 675\\ 576\le a+50\lt 625}\\ \qquad \Rightarrow 兩區間[626,675),[576,625)無交集 \\,故選\bbox[red, 2pt]{(D)}$$
解答:$$f(x)=9x^2+31x+4 =(9x+1)(x+4) \\ \Rightarrow 9\times 31^2+31\times 37+4 =f(31)=280\times 35 =a =2^3\times 5^2\times 7^2\\ \Rightarrow 符合條件的正因數: 10\lt 14,20,25,28\lt 30 \Rightarrow 14+20+ 25+ 28= 87,故選\bbox[red, 2pt]{(A)}$$
解答:$$\begin{array}{} 品項& 中杯& 折扣後& 每毫升價格& 大杯& 折扣後& 每毫升價格\\\hline 義式咖啡& 35& 32& 0.089& 50& 45& 0.094\\ 拿鐵& 50& 47& 0.13 & 65& 60& 0.125\\ 卡布奇諾& 45& 42& 0.117& 60& 55 & 0.114\\\hline \end{array} \\由上表可知:義式咖咖大杯(0.094)比中杯(0.089)貴,故選\bbox[red, 2pt]{(A)}$$
解答:$$\cases{a=\sqrt 3+1\\ b=\sqrt 3-1} \Rightarrow ab=2 \Rightarrow (\sqrt 3+1)^{-3} (\sqrt 3-1)^{-4} =(ab)^{-3}b^{-1}= {1\over 8b}={1\over 8}\cdot {\sqrt 3+1\over 2} \\={\sqrt 3+1\over 16} \approx {2.732\over 16} =0.17,故選\bbox[red, 2pt]{(C)}$$
解答:$$x=\sin \theta \Rightarrow dx =\cos \theta \;d\theta \Rightarrow \int_0^1 \sqrt{1-x^2}\,dx = \int_0^{\pi/2} \cos^2 \theta \,d\theta ={1\over 2}\int_0^{\pi/2} (\cos 2\theta +1)\,d\theta \\= {1\over 2} \left. \left[ {1\over 2}\sin 2\theta+\theta\right] \right|_0^{\pi/2} ={\pi\over 4},故選\bbox[red, 2pt]{(B)}$$
解答:$$公差d= a_2-a_1={1\over 4} \\ a_1,a_3,a_6成等比 \Rightarrow a_3^2=a_1a_6 \Rightarrow (a_1+2d)^2=a_1(a_1+5d) \Rightarrow (a_1+{1\over 2})^2=a_1(a_1+ {5\over 4}) \\ \Rightarrow a_1=1 \Rightarrow \cases{ a_1:a_2=1:5/4=4:5\\ a_1:a_3=1:3/2=2:3},故選\bbox[red, 2pt]{(D)}$$
解答:$$\cases{甲班捐書量=6+14+11(x-3)=11x-13\\ 乙班捐書量= 6+24+10(y-4)= 10y-10} \Rightarrow \cases{250\le 11x-13\le 300\\ 250\le 10y-10\le 300} \Rightarrow \cases{24\le x\le 28\\ 26\le y\le 31} \\又 11x-13=10y-10+13 \Rightarrow 11x-10y=16 \Rightarrow x={10y+16\over 11}為一整數\\ \Rightarrow \cases{y=26,28,29,30,31 \Rightarrow x不是整數\\ y=27 \Rightarrow x=26} \Rightarrow \cases{甲班捐書26人\\ 乙班捐書27人\\ 甲班捐書量11x-13=273本\\ 乙班捐書量10y-10=260本}\\,故選\bbox[red, 2pt]{(C)}$$
解答:$$y=ax^2+a^2x-1=a(x^2+ax)-1=a(x^2+ax+{a^2\over 4})-1-{a^3\over 4} =a(x+{a\over 2})^2-{a^3+4\over 4} \\ \Rightarrow 頂點坐標(-{a\over 2},-{a^3+4\over 4}) \Rightarrow \cases{a\gt 0 \Rightarrow 第三象限\\ a\lt 0 \Rightarrow 第一或四象限} \Rightarrow 不可能在第二象限,故選\bbox[red, 2pt]{(B)}$$
解答:$$x(y^2+z^2) +y(z^2+x^2)+ z(x^2+y^2) +2xyz \\ =xy^2+xz^2+yz^2+ x^2y +x^2z+ y^2z +2xyz \\= xy(x+y)+ z^2(x+y)+ z(x^2+y^2+2xy) \\=(xy+z^2)(x+y)+z(x+y)^2= (x+y)(xy+z^2+xz+yz) \\=(x+y)(x(y+z)+z(y+z))=(x+y)(x+z)(y+z),故選\bbox[red, 2pt]{(A)}$$
解答:
$$假設\cases{\overline{AE}=a\\ \overline{BE}=b\\ \overline{CE}=c\\ \overline{DE}=d},由於\overline{AB} =\overline{BC} \Rightarrow \angle BAE=\angle BCA={180-42-44\over 2}=47^\circ\\ 又對同弧的圓周角相等\Rightarrow \cases{ \angle ACD =\angle ABD=44^\circ\\ \angle CAD=\angle DBC=42^\circ\\ \angle BDC=\angle BAC=47^\circ\\ \angle ADB=\angle ACB=47^\circ},大角對大邊\Rightarrow \cases{b\gt a\\ b\gt c\\ a\gt d\\ c\gt d \\ \overline{AD}\gt \overline{CD}} \\ \Rightarrow b=\overline{BE}最長,又\overline{DE}為\angle ADC的角平分線 \Rightarrow {a\over c}={ \overline{AD}\over \overline{DC}} \Rightarrow a\gt c,故選\bbox[red, 2pt]{(B)}$$
解答:$$S=1+3+5+\cdots+n \Rightarrow \cases{n=13=2\times 7-1 \Rightarrow S=49\\ n=15=2\times8-1\Rightarrow S=64} \Rightarrow 45\lt 52\lt 55 \\ \Rightarrow 52=49+3 \Rightarrow {3\over 8},故選\bbox[red, 2pt]{(B)}$$
解答:



解答:$$S=1+3+5+\cdots+n \Rightarrow \cases{n=13=2\times 7-1 \Rightarrow S=49\\ n=15=2\times8-1\Rightarrow S=64} \Rightarrow 45\lt 52\lt 55 \\ \Rightarrow 52=49+3 \Rightarrow {3\over 8},故選\bbox[red, 2pt]{(B)}$$
解答:

$$假設\angle POA=\theta \Rightarrow \angle QPD= \angle RQE=\theta \Rightarrow \sin \angle QPD={\overline{QD} \over \overline{PQ}} \Rightarrow \sin \theta={1\over 2} \Rightarrow \theta=30^\circ \\ \Rightarrow \overline{RE} = \overline{RQ}\sin 30^\circ \Rightarrow r-3={r+3\over 2} \Rightarrow r=9 \Rightarrow \overline{BC}=(r+3)\cos 30^\circ=12\cdot {\sqrt 3\over 2}= 6\sqrt 3\\,故選\bbox[red, 2pt]{(C)}$$
解答:$$假設\cases{x'=x-1\\ y'=y-2\\ z'=z-3},則x+y+z=20 \Rightarrow x'+1+y'+2+z'+3=20 \Rightarrow x'+y'+z'=14 \\ \Rightarrow 有H^3_{14} =C^{16}_{14}=120組整數解,故選\bbox[red, 2pt]{(A)}$$
解答:
解答:

$$假設圓半徑為r,由於\angle PQR=15^\circ \Rightarrow \angle POR=30^\circ \Rightarrow \overline{OP}={\sqrt 3\over 2}\overline{OR} \Rightarrow r={\sqrt 3\over 2}(18-r) \\ \Rightarrow r=36\sqrt 3-54 \Rightarrow \overline{PR}= {r\over \sqrt 3}=36-18\sqrt 3,故選\bbox[red, 2pt]{(D)}$$
解答:$$\begin{array}{|c|c|}\hline p&q\\\hline r& s\\\hline\end{array} =\begin{array}{|c|c|}\hline ab&a(b+1)\\\hline (a+1)b & (a+1)(b+1)\\\hline\end{array} \\ p+q+r+s =ab+a(b+1)+ (a+1)b+(a+1)(b+1) =a(2b+1)+ (a+1)(2b+1) \\= (2a+1)(2b+1)= 91=13\times 7 \Rightarrow (a,b)=(3,6)或(6,3) \Rightarrow a+b=9,故選\bbox[red, 2pt]{(C)}$$
解答:
解答:$$\begin{array}{|c|c|}\hline p&q\\\hline r& s\\\hline\end{array} =\begin{array}{|c|c|}\hline ab&a(b+1)\\\hline (a+1)b & (a+1)(b+1)\\\hline\end{array} \\ p+q+r+s =ab+a(b+1)+ (a+1)b+(a+1)(b+1) =a(2b+1)+ (a+1)(2b+1) \\= (2a+1)(2b+1)= 91=13\times 7 \Rightarrow (a,b)=(3,6)或(6,3) \Rightarrow a+b=9,故選\bbox[red, 2pt]{(C)}$$
解答:

$$正三角形的四心是同一點,因此假設正方形頂點坐標\cases{P(1,1)\\ Q(-1,1)\\ R(-1,-1)\\ S(1,-1)},\\則乙,丙,丁,戊的重心坐標\cases{A(0,1+{\sqrt 3\over 3})\\ B(-1-{\sqrt 3\over 3},0)\\ C(0,-1-{\sqrt 3\over 3})\\ D(1+{\sqrt 3\over 3},0)} \\ \Rightarrow \overline{AB}=\sqrt{8+4\sqrt 3\over 3} \Rightarrow {正方形ABCD面積\over 甲面積} ={ (8+4\sqrt 3)/3\over 4} ={2+\sqrt 3\over 3},故選\bbox[red, 2pt]{(A)}$$
=========== END ================

















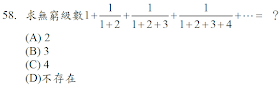



























沒有留言:
張貼留言