113學年度中區縣市政府教師甄選策略聯盟
【科目名稱:國中數學】
選擇題【共50題,每題2分,共100分】請以2B鉛筆於答案卡上作答,單選題;答錯不倒扣。
解答:$$\begin{array}{c|cccccc} x& 2^{(1\times 2)/2} & 2^{(2\times 3)/2} & 2^{(3\times 4)/2} & 2^{(4\times 5)/2} & 2^{(5\times 6)/2} & 2^{(6\times 7)/2} & 2^{(7\times 8)/2} & 2^{(8\times 9)/2} \\\hline \mod 7 & 2 & 1& 1& 2& 1& 1& 2& 1\end{array} \\ \Rightarrow 餘數為2,1,1,循環,共99項,餘數總和=(2+1+1)\times 33= 132 = 6\mod 7,故選\bbox[red, 2pt]{(D)}$$
解答:

$$有兩塊區域,面積= \int_0^1 (x-x^2)\,dx +\int_{1}^{2} (x^2-x)\,dx = \left. \left[ {1\over 2}x^2 -{1\over 3}x^3 \right] \right|_0^1+ \left. \left[ {1\over 3}x^3-{1\over 2}x^2 \right] \right|_1^2 \\ ={1\over 6}+{5\over 6}=1,故選\bbox[red, 2pt]{(C)}$$
解答:$$(A)\times: f(x)=(-1)^n \Rightarrow \lim_{x\to a}|f(x)|=1, 但\lim_{x\to a}f(x) 不存在\\ (B)\times:\cases{f(x)=1/(x-a)\\ g(x)=-1/(x-a)} \Rightarrow \lim_{x\to a}(f(x)+g(x))=0存在,但\lim_{x\to a}f(x)不存在\\ (C)\times: \cases{f(x)=x^2\\ g(x)=1/x^2} \Rightarrow \cases{\lim_{x\to 2} {f(x)\over g(x)} =2^4=16 =\alpha\\ \lim_{x\to 2} {1\over f(x)}={1\over 4} =\beta} \Rightarrow \lim_{x\to 2} g(x)={1\over 4} \ne {1\over 64}={\beta\over \alpha}\\,故選\bbox[red, 2pt]{(D)}$$
解答:
解答:$$(A)\times: f(x)=(-1)^n \Rightarrow \lim_{x\to a}|f(x)|=1, 但\lim_{x\to a}f(x) 不存在\\ (B)\times:\cases{f(x)=1/(x-a)\\ g(x)=-1/(x-a)} \Rightarrow \lim_{x\to a}(f(x)+g(x))=0存在,但\lim_{x\to a}f(x)不存在\\ (C)\times: \cases{f(x)=x^2\\ g(x)=1/x^2} \Rightarrow \cases{\lim_{x\to 2} {f(x)\over g(x)} =2^4=16 =\alpha\\ \lim_{x\to 2} {1\over f(x)}={1\over 4} =\beta} \Rightarrow \lim_{x\to 2} g(x)={1\over 4} \ne {1\over 64}={\beta\over \alpha}\\,故選\bbox[red, 2pt]{(D)}$$
解答:
$$\overline{AB}與 \overline{CD}均為直徑\Rightarrow O為圓心,假設半徑為r,\overline{CE}=a\\ \triangle DOF \sim \triangle DEC (AAA) \Rightarrow {\overline{OD} \over \overline{FD}} ={\overline{DE} \over \overline{CD}} \Rightarrow {r\over 6} ={8\over 2r} \Rightarrow r=2\sqrt 6 \\ 直角\triangle CDE: \overline{CD}^2= \overline{DE}^2+ \overline{CE}^2 \Rightarrow 4r^2=8^2+a^2 \Rightarrow a=4\sqrt 2\\,故選\bbox[red, 2pt]{(D)}$$
解答:$$\cases{\alpha+\beta=p \\ \alpha\beta=-276p} \Rightarrow (\beta-\alpha)^2 =(\beta+\alpha)^2-4\alpha \beta=p^2+1104p \\ \Rightarrow \beta-\alpha=\sqrt{p^2+1104p} =\sqrt{p^2+2^4\cdot 3\cdot 23\cdot p} =\sqrt{23^2\cdot 7^2} \text{ (if }p=23) =23\cdot 7=161,故選\bbox[red, 2pt]{(D)}$$
解答:$$\cases{a\gt 0\\ b\gt 0} \Rightarrow \cases{2a+b=10\\ a=12} \Rightarrow b\lt 0\;矛盾; 同理,\cases{a<0\\ b\gt0}或\cases{a\lt 0\\ b\lt 0}皆矛盾\\ \cases{a\gt 0\\ b\lt 0} \Rightarrow \cases{2a+b=10\\ a-2b=12} \Rightarrow \cases{a=32/5\\ b=-14/5} \Rightarrow a+b={18\over 5},故選\bbox[red, 2pt]{(A)}$$
解答:$$\cos A=\cos 120^\circ=-{1\over 2} ={4^2+2^2-\overline{BC}^2\over 2\cdot 2\cdot 4} \Rightarrow \overline{BC}=2\sqrt 7\\ \overline{AD}為\angle A的角平分線 \Rightarrow {\overline{AB}\over \overline{AC}} ={\overline{BD} \over \overline{DC}} \Rightarrow \cases{\overline{BC}=4\sqrt 7/3\\ \overline{CD}=2\sqrt 7/3} \\ \cos \angle CAD=\cos 60^\circ={1\over 2}={4^2+ \overline{AD}^2-112/9 \over 8\overline{AD}} \Rightarrow \overline{AD}= {4\over 3}, {8\over 3}(不合),故選\bbox[red, 2pt]{(B)}$$
解答:$$A=\begin{bmatrix}0 & 2 & 4 & 2 & 2\\4 & 4 & 4 & 8 & 0\\8 & 2 & 0 & 10 & 2\\6 & 3 & 2 & 9 & 1 \end{bmatrix} \xrightarrow{R_1/2 \to R_1,R_2/4\to R_2} \left[\begin{matrix}0 & 1 & 2 & 1 & 1\\1 & 1 & 1 & 2 & 0\\8 & 2 & 0 & 10 & 2\\6 & 3 & 2 & 9 & 1\end{matrix}\right] \xrightarrow{R_3-8R_2\to R_3,R_4-6R_2\to R_4} \\\left[\begin{matrix}0 & 1 & 2 & 1 & 1\\1 & 1 & 1 & 2 & 0\\0 & -6 & -8 & -6 & 2\\0 & -3 & -4 & -3 & 1\end{matrix}\right] \xrightarrow{R_3+6R_1\to R_3,R_4+3R_1\to R_4} \left[\begin{matrix}0 & 1 & 2 & 1 & 1\\1 & 1 & 1 & 2 & 0\\0 & 0 & 4 & 0 & 8\\0 & 0 & 2 & 0 & 4\end{matrix}\right] \xrightarrow{R_1\leftrightarrow R_2} \\\left[\begin{matrix}1 & 1 & 1 & 2 & 0\\0 & 1 & 2 & 1 & 1\\0 & 0 & 4 & 0 & 8\\0 & 0 & 2 & 0 & 4\end{matrix}\right] \xrightarrow{R_1-R_2\to R_1, R_3/4 \to R_3} \left[\begin{matrix}1 & 0 & -1 & 1 & -1\\0 & 1 & 2 & 1 & 1\\0 & 0 & 1 & 0 & 2\\0 & 0 & 2 & 0 & 4\end{matrix}\right]\\ \xrightarrow{R_1+R_3 \to R_1,R_2-2R_3\to R_2, R_4-2R_2\to R_4} \left[\begin{matrix}1 & 0 & 0 & 1 & 1\\0 & 1 & 0 & 1 & -3\\0 & 0 & 1 & 0 & 2\\0 & 0 & 0 & 0 & 0\end{matrix}\right] \Rightarrow \text{rank}(A)=3,故選\bbox[red, 2pt]{(C)}$$
解答:$${\sin 3\theta\over \sin \theta} ={-4\sin^3 \theta+ 3\sin \theta\over \sin \theta} = -4\sin^2\theta+3={7\over 3} \Rightarrow \sin ^2\theta={1\over 6} \Rightarrow \sin \theta={1\over \sqrt 6}\\ \Rightarrow \cos \theta={\sqrt 5\over \sqrt 6} \Rightarrow {\cos 3\theta\over \cos \theta} ={4\cos^3\theta- 3\cos \theta\over \cos \theta} =4\cos^2\theta-3=4\cdot {5\over 6}-3={1\over 3},故選\bbox[red, 2pt]{(A)}$$
解答:
解答:$$\cases{\alpha+\beta=p \\ \alpha\beta=-276p} \Rightarrow (\beta-\alpha)^2 =(\beta+\alpha)^2-4\alpha \beta=p^2+1104p \\ \Rightarrow \beta-\alpha=\sqrt{p^2+1104p} =\sqrt{p^2+2^4\cdot 3\cdot 23\cdot p} =\sqrt{23^2\cdot 7^2} \text{ (if }p=23) =23\cdot 7=161,故選\bbox[red, 2pt]{(D)}$$
解答:$$\cases{a\gt 0\\ b\gt 0} \Rightarrow \cases{2a+b=10\\ a=12} \Rightarrow b\lt 0\;矛盾; 同理,\cases{a<0\\ b\gt0}或\cases{a\lt 0\\ b\lt 0}皆矛盾\\ \cases{a\gt 0\\ b\lt 0} \Rightarrow \cases{2a+b=10\\ a-2b=12} \Rightarrow \cases{a=32/5\\ b=-14/5} \Rightarrow a+b={18\over 5},故選\bbox[red, 2pt]{(A)}$$
解答:$$\cos A=\cos 120^\circ=-{1\over 2} ={4^2+2^2-\overline{BC}^2\over 2\cdot 2\cdot 4} \Rightarrow \overline{BC}=2\sqrt 7\\ \overline{AD}為\angle A的角平分線 \Rightarrow {\overline{AB}\over \overline{AC}} ={\overline{BD} \over \overline{DC}} \Rightarrow \cases{\overline{BC}=4\sqrt 7/3\\ \overline{CD}=2\sqrt 7/3} \\ \cos \angle CAD=\cos 60^\circ={1\over 2}={4^2+ \overline{AD}^2-112/9 \over 8\overline{AD}} \Rightarrow \overline{AD}= {4\over 3}, {8\over 3}(不合),故選\bbox[red, 2pt]{(B)}$$
解答:$$A=\begin{bmatrix}0 & 2 & 4 & 2 & 2\\4 & 4 & 4 & 8 & 0\\8 & 2 & 0 & 10 & 2\\6 & 3 & 2 & 9 & 1 \end{bmatrix} \xrightarrow{R_1/2 \to R_1,R_2/4\to R_2} \left[\begin{matrix}0 & 1 & 2 & 1 & 1\\1 & 1 & 1 & 2 & 0\\8 & 2 & 0 & 10 & 2\\6 & 3 & 2 & 9 & 1\end{matrix}\right] \xrightarrow{R_3-8R_2\to R_3,R_4-6R_2\to R_4} \\\left[\begin{matrix}0 & 1 & 2 & 1 & 1\\1 & 1 & 1 & 2 & 0\\0 & -6 & -8 & -6 & 2\\0 & -3 & -4 & -3 & 1\end{matrix}\right] \xrightarrow{R_3+6R_1\to R_3,R_4+3R_1\to R_4} \left[\begin{matrix}0 & 1 & 2 & 1 & 1\\1 & 1 & 1 & 2 & 0\\0 & 0 & 4 & 0 & 8\\0 & 0 & 2 & 0 & 4\end{matrix}\right] \xrightarrow{R_1\leftrightarrow R_2} \\\left[\begin{matrix}1 & 1 & 1 & 2 & 0\\0 & 1 & 2 & 1 & 1\\0 & 0 & 4 & 0 & 8\\0 & 0 & 2 & 0 & 4\end{matrix}\right] \xrightarrow{R_1-R_2\to R_1, R_3/4 \to R_3} \left[\begin{matrix}1 & 0 & -1 & 1 & -1\\0 & 1 & 2 & 1 & 1\\0 & 0 & 1 & 0 & 2\\0 & 0 & 2 & 0 & 4\end{matrix}\right]\\ \xrightarrow{R_1+R_3 \to R_1,R_2-2R_3\to R_2, R_4-2R_2\to R_4} \left[\begin{matrix}1 & 0 & 0 & 1 & 1\\0 & 1 & 0 & 1 & -3\\0 & 0 & 1 & 0 & 2\\0 & 0 & 0 & 0 & 0\end{matrix}\right] \Rightarrow \text{rank}(A)=3,故選\bbox[red, 2pt]{(C)}$$
解答:$${\sin 3\theta\over \sin \theta} ={-4\sin^3 \theta+ 3\sin \theta\over \sin \theta} = -4\sin^2\theta+3={7\over 3} \Rightarrow \sin ^2\theta={1\over 6} \Rightarrow \sin \theta={1\over \sqrt 6}\\ \Rightarrow \cos \theta={\sqrt 5\over \sqrt 6} \Rightarrow {\cos 3\theta\over \cos \theta} ={4\cos^3\theta- 3\cos \theta\over \cos \theta} =4\cos^2\theta-3=4\cdot {5\over 6}-3={1\over 3},故選\bbox[red, 2pt]{(A)}$$

$$\overline{AE}為直徑\Rightarrow \angle ACE=90^\circ \Rightarrow \overline{CE}=\sqrt{12^2-(4\sqrt 5)^2} =8\\ 假設小圓半徑r \Rightarrow \overline{AD}=12-2r \Rightarrow \overline{CD}^2=\overline{AC}^2-\overline{AD}^2=\overline{CE}^2-\overline{DE}^2 \\ \Rightarrow (4\sqrt 5)^2-(12-2r)^2= 8^2-(2r)^2 \Rightarrow r={8\over 3},故選\bbox[red, 2pt]{(C)}$$

解答:

$$\angle APB= \angle APC=\angle CPB=120^\circ \Rightarrow P為費馬點\text{(Fermat point)}\\ 因此作正\triangle ACD,則D,P,B三點共線,且\overline{PA} +\overline{PB}+ \overline{PC} =\overline{DB}\\ \cos \angle APC=\cos 120^\circ=-{1\over 2} ={8^2+6^2-\overline{AC}^2 \over 2\cdot 6\cdot 8} \Rightarrow \overline{AC} =2\sqrt{37}\\ 假設\cases{C(0,0)\\ E=\overline{PE}\cap \overline{AC}},由於\angle CPA=120^\circ \Rightarrow \angle APE=\angle EPC=60^\circ \Rightarrow \overline{EP}是\angle APC的角平分線\\ \Rightarrow {\overline{AE}\over \overline{EC}} ={\overline{PA} \over \overline{PC}} ={4\over 3} \Rightarrow \overline{EC}=2\sqrt{37}\cdot {3\over 3+4} ={6\over 7}\sqrt{37} \Rightarrow E(0,{6\over 7}\sqrt{37}) \\ \overline{AC} =2\sqrt{37} \Rightarrow D(-\sqrt{111},\sqrt{37}) \Rightarrow L=\overleftrightarrow{DE}: y=-{\sqrt{37}\over 8\sqrt{111}}x+{6\over 7}\sqrt{37} \Rightarrow B(6\sqrt{111},0) \\ \Rightarrow \overline{DB}=74 \Rightarrow \overline{PB}=74-6-8=60,故選\bbox[red, 2pt]{(D)}$$
解答:$$b=c \Rightarrow R={ab^2\over 2b}={a\over 2} \Rightarrow a=2R (直徑) \Rightarrow 等腰直角三角形,故選\bbox[red, 2pt]{(A)}$$
解答:$$f(x)=xg(x), 其中g(x)={(x-1)(x-2) \cdots (x-2024)\over (x+1)(x+2) \cdots (x+2024)} \\ \Rightarrow f'(x)=g(x)+xg'(x) \Rightarrow f'(0)= g(0)={2024!\over 2024!} =1,故選\bbox[red, 2pt]{(C)}$$
解答:$$f(x)=x^4+2x^3-3x^2+2x-1 \Rightarrow f'(x)=4x^3+6x^2-6x+2\\ \lim_{h\to 0}{f(1+3h)-f(1-2h)\over h} =\lim_{h\to 0}{(f(1+3h)-f(1-2h) )'\over (h)'} = \lim_{h\to 0}{3f'(1+3h)+2f'(1-2h)\over 1} \\=3f''(1)+2f'(1)= 3(4+6-6+2)+2(4+6-6+2)=18+12=30,故選\bbox[red, 2pt]{(D)}$$
解答:$$依均值定理,故選\bbox[red, 2pt]{(A)}$$
解答:$$\int_0^{\pi/2} \cos x\,dx =1 \Rightarrow 平均值={1\over \pi/2}= {2\over \pi},故選\bbox[red, 2pt]{(A)}$$
解答:$$\cases{\tan \alpha+\tan\beta=p\\ \tan \alpha\tan\beta =q} \Rightarrow \cases{{1\over \cot \alpha}+{1\over \cot\beta} =p\\ {1\over \cot \alpha \cot \beta}=q} \Rightarrow \cases{ \cot \alpha+\cot \beta=p/q \\\cot \alpha \cot \beta=1/q} \\ \Rightarrow rs=(\cot \alpha+\cot \beta)(\cot \alpha \cot \beta)={ p\over q} \cdot {1\over q} ={p\over q^2},故選\bbox[red, 2pt]{(C)}$$
解答:$${(\log_a x)\cdot (\log_x{b\over a}) \over (\log_x b)(\log_{ab} x)} ={(\log_a x)\cdot (\log_x b-\log_x a) \over (\log_x b)({1\over \log_x ab })} = {\log_a b-1\over \log_{ab}b} \\={\log_a b-1\over {1\over \log_b a+1}} =(\log_b a+1)(\log_a b-1)=1-\log_ba+\log_a b-1=-{1\over 10}+10 ={99\over10},故選\bbox[red, 2pt]{(B)}$$
解答:$${1+2\sqrt 3+\sqrt 5\over (1+\sqrt 3) (\sqrt 3+\sqrt 5)} +{3+2\sqrt 7+ \sqrt 5\over (\sqrt 5+\sqrt 7) (\sqrt 7+3)} ={(1+\sqrt 3)+(\sqrt 3+\sqrt 5)\over (1+\sqrt 3) (\sqrt 3+\sqrt 5)} +{(3+\sqrt 7)+ (\sqrt 7+\sqrt 5)\over (\sqrt 5+\sqrt 7) (\sqrt 7+3)} \\={1\over \sqrt 3+\sqrt 5} +{1\over 1+\sqrt 3} +{1\over \sqrt 5+\sqrt 7} +{1\over \sqrt 7+3}={1\over 2}\left(\sqrt 5-\sqrt 3+\sqrt 3-1+\sqrt 7-\sqrt 5+3-\sqrt 7 \right) \\=1,故選\bbox[red, 2pt]{(B)}$$
解答:$$\sum_{n=1}^\infty {\sqrt{n+1}-\sqrt n\over \sqrt{n^2+n}} =\sum_{n=1}^\infty \left( {1\over \sqrt{n}} -{1\over \sqrt{n+1}}\right) =1-{1\over \sqrt 2}+{1\over \sqrt 2}-{1\over \sqrt 3}+{1\over \sqrt 3}-{1\over \sqrt 4}+\cdots \\=1,故選\bbox[red, 2pt]{(A)}$$
解答:$$a=\sqrt 2+b \Rightarrow a^2=\sqrt 2a+ab \Rightarrow 2ab=2a^2-2\sqrt 2a \Rightarrow 2a^2-2\sqrt 2a+2\sqrt 2 c^2+1=0 \\ \Rightarrow 2(a-{\sqrt 2\over 2})^2+2\sqrt 2c^2=0 \Rightarrow \cases{a=\sqrt 2/2\\ c=0} \Rightarrow b=a-\sqrt 2=-{\sqrt 2 \over 2} \\ \Rightarrow \cases{a=\sqrt 2/2\\ b=-\sqrt 2/2\\ c=0} \Rightarrow a+b+c=0,故選\bbox[red, 2pt]{(D)}$$
解答:$$\cos x={1\over 2}(e^{ix}+e^{-ix}) \Rightarrow \int_0^\infty e^{-x}\cos x\,dx ={1 \over 2} \int_0^\infty \left(e^{(i-1)x}+e^{-(i+1)x} \right)\,dx \\={1\over 2} \left. \left[ {1\over i-1}e^{(i-1)x}-{1\over i+1}e^{-(i+1)x}\right] \right|_0^\infty ={1\over 2}\left({1\over i+1}-{1\over i-1} \right)={1\over 2}\cdot 1={1\over 2},故選\bbox[red, 2pt]{(C)}$$
解答:$$凸n邊形內角和=f(n)=180(n-2) \\\Rightarrow \cases{f(12)=1800\lt 2024,不合\\ f(13) =1980\lt2024,不合\\ f(14) =2160 \Rightarrow 另一角度數=2160-2024=136度\\ f(15)=2340 \Rightarrow 另一角度數=2340-2024=316度,不合},故選\bbox[red, 2pt]{(C)}$$
解答:$$\begin{vmatrix} 1& 4& 1& -3\\ 2& 10 & 0 &1 \\ 0 & 0& 2& 2\\ 0 & 0 &-2& 1\end{vmatrix} \xrightarrow{R_2-2R_1\to R_2} \begin{vmatrix} 1& 4& 1& -3\\ 0& 2 & -2 &7 \\ 0 & 0& 2& 2\\ 0 & 0 &-2& 1\end{vmatrix} =\begin{vmatrix} 2 & -2 &7 \\ 0& 2& 2\\ 0 &-2& 1\end{vmatrix} =2 \begin{vmatrix} 2& 2\\ -2& 1\end{vmatrix}=12,故選\bbox[red, 2pt]{(D)}$$
解答:$$(A) \bigcirc:\cases{\overrightarrow{AB} =(1,2,-1) \\ \overrightarrow{AC} =(-2,2,2) } \Rightarrow \overrightarrow{AB} \cdot \overrightarrow{AC} =0 \Rightarrow \angle BAC={\pi\over 2} \\(B)\bigcirc:\overrightarrow{AB} =(2,1,-1)-(1,-1,0)=(1,2,-1) \\(C)\bigcirc: \overrightarrow{AB} \times \overrightarrow{AC} =\begin{vmatrix}\vec i& \vec j&\vec k \\ 1& 2& -1\\ -2& 2& 2\end{vmatrix} =6\vec i+0\vec j+6\vec k \\(D)\times: {1\over 2}\Vert\overrightarrow{AB} \times \overrightarrow{AC} \Vert = 3\sqrt 2\ne 2\sqrt 2\\,故選\bbox[red, 2pt]{(D)}$$
解答:$$7^{10} = 1 \text{ mod }11 \Rightarrow 7^{223} =(7^{10})^{22}\cdot 7^3 =7^3 \text{ mod }11 =2\text{ mod }11 ,故選\bbox[red, 2pt]{(A)}$$
解答:$$0.\bar 3 ={3\over 9}={1\over 3},故選\bbox[red, 2pt]{(B)}$$
解答:$$\sqrt 5\approx2.236 \Rightarrow {1+\sqrt 5\over 4} \approx 0.81,故選\bbox[red, 2pt]{(C)}$$
解答:$$3f(1)+5f(1)=2+1 \Rightarrow f(1)={3\over 8}=0.375,故選\bbox[red, 2pt]{(D)}$$
解答:$$\int_0^1 {x^2\over 1+x^2}\,dx =\int_0^1 \left( 1-{1\over 1+x^2}\right)\,dx =\left. \left[ x-\tan^{-1}x\right] \right|_0^1 =1-{\pi\over 4},故選\bbox[red, 2pt]{(A)}$$
解答:$$只有四種可能\cases{1,1,2,3\\ 1,2,2,3\\ 1,2,3,3}排列數皆為{4!\over 2!}=12,因此共有12\times 3=36種,故選\bbox[red, 2pt]{(D)}$$
解答:$$f(x)=xg(x), 其中g(x)={(x-1)(x-2) \cdots (x-2024)\over (x+1)(x+2) \cdots (x+2024)} \\ \Rightarrow f'(x)=g(x)+xg'(x) \Rightarrow f'(0)= g(0)={2024!\over 2024!} =1,故選\bbox[red, 2pt]{(C)}$$
解答:$$f(x)=x^4+2x^3-3x^2+2x-1 \Rightarrow f'(x)=4x^3+6x^2-6x+2\\ \lim_{h\to 0}{f(1+3h)-f(1-2h)\over h} =\lim_{h\to 0}{(f(1+3h)-f(1-2h) )'\over (h)'} = \lim_{h\to 0}{3f'(1+3h)+2f'(1-2h)\over 1} \\=3f''(1)+2f'(1)= 3(4+6-6+2)+2(4+6-6+2)=18+12=30,故選\bbox[red, 2pt]{(D)}$$
解答:$$依均值定理,故選\bbox[red, 2pt]{(A)}$$
解答:$$\int_0^{\pi/2} \cos x\,dx =1 \Rightarrow 平均值={1\over \pi/2}= {2\over \pi},故選\bbox[red, 2pt]{(A)}$$
解答:$${(\log_a x)\cdot (\log_x{b\over a}) \over (\log_x b)(\log_{ab} x)} ={(\log_a x)\cdot (\log_x b-\log_x a) \over (\log_x b)({1\over \log_x ab })} = {\log_a b-1\over \log_{ab}b} \\={\log_a b-1\over {1\over \log_b a+1}} =(\log_b a+1)(\log_a b-1)=1-\log_ba+\log_a b-1=-{1\over 10}+10 ={99\over10},故選\bbox[red, 2pt]{(B)}$$
解答:$${1+2\sqrt 3+\sqrt 5\over (1+\sqrt 3) (\sqrt 3+\sqrt 5)} +{3+2\sqrt 7+ \sqrt 5\over (\sqrt 5+\sqrt 7) (\sqrt 7+3)} ={(1+\sqrt 3)+(\sqrt 3+\sqrt 5)\over (1+\sqrt 3) (\sqrt 3+\sqrt 5)} +{(3+\sqrt 7)+ (\sqrt 7+\sqrt 5)\over (\sqrt 5+\sqrt 7) (\sqrt 7+3)} \\={1\over \sqrt 3+\sqrt 5} +{1\over 1+\sqrt 3} +{1\over \sqrt 5+\sqrt 7} +{1\over \sqrt 7+3}={1\over 2}\left(\sqrt 5-\sqrt 3+\sqrt 3-1+\sqrt 7-\sqrt 5+3-\sqrt 7 \right) \\=1,故選\bbox[red, 2pt]{(B)}$$
解答:$$\sum_{n=1}^\infty {\sqrt{n+1}-\sqrt n\over \sqrt{n^2+n}} =\sum_{n=1}^\infty \left( {1\over \sqrt{n}} -{1\over \sqrt{n+1}}\right) =1-{1\over \sqrt 2}+{1\over \sqrt 2}-{1\over \sqrt 3}+{1\over \sqrt 3}-{1\over \sqrt 4}+\cdots \\=1,故選\bbox[red, 2pt]{(A)}$$
解答:$$a=\sqrt 2+b \Rightarrow a^2=\sqrt 2a+ab \Rightarrow 2ab=2a^2-2\sqrt 2a \Rightarrow 2a^2-2\sqrt 2a+2\sqrt 2 c^2+1=0 \\ \Rightarrow 2(a-{\sqrt 2\over 2})^2+2\sqrt 2c^2=0 \Rightarrow \cases{a=\sqrt 2/2\\ c=0} \Rightarrow b=a-\sqrt 2=-{\sqrt 2 \over 2} \\ \Rightarrow \cases{a=\sqrt 2/2\\ b=-\sqrt 2/2\\ c=0} \Rightarrow a+b+c=0,故選\bbox[red, 2pt]{(D)}$$
解答:$$\cos x={1\over 2}(e^{ix}+e^{-ix}) \Rightarrow \int_0^\infty e^{-x}\cos x\,dx ={1 \over 2} \int_0^\infty \left(e^{(i-1)x}+e^{-(i+1)x} \right)\,dx \\={1\over 2} \left. \left[ {1\over i-1}e^{(i-1)x}-{1\over i+1}e^{-(i+1)x}\right] \right|_0^\infty ={1\over 2}\left({1\over i+1}-{1\over i-1} \right)={1\over 2}\cdot 1={1\over 2},故選\bbox[red, 2pt]{(C)}$$
解答:$$凸n邊形內角和=f(n)=180(n-2) \\\Rightarrow \cases{f(12)=1800\lt 2024,不合\\ f(13) =1980\lt2024,不合\\ f(14) =2160 \Rightarrow 另一角度數=2160-2024=136度\\ f(15)=2340 \Rightarrow 另一角度數=2340-2024=316度,不合},故選\bbox[red, 2pt]{(C)}$$
解答:$$\begin{vmatrix} 1& 4& 1& -3\\ 2& 10 & 0 &1 \\ 0 & 0& 2& 2\\ 0 & 0 &-2& 1\end{vmatrix} \xrightarrow{R_2-2R_1\to R_2} \begin{vmatrix} 1& 4& 1& -3\\ 0& 2 & -2 &7 \\ 0 & 0& 2& 2\\ 0 & 0 &-2& 1\end{vmatrix} =\begin{vmatrix} 2 & -2 &7 \\ 0& 2& 2\\ 0 &-2& 1\end{vmatrix} =2 \begin{vmatrix} 2& 2\\ -2& 1\end{vmatrix}=12,故選\bbox[red, 2pt]{(D)}$$
解答:$$(A) \bigcirc:\cases{\overrightarrow{AB} =(1,2,-1) \\ \overrightarrow{AC} =(-2,2,2) } \Rightarrow \overrightarrow{AB} \cdot \overrightarrow{AC} =0 \Rightarrow \angle BAC={\pi\over 2} \\(B)\bigcirc:\overrightarrow{AB} =(2,1,-1)-(1,-1,0)=(1,2,-1) \\(C)\bigcirc: \overrightarrow{AB} \times \overrightarrow{AC} =\begin{vmatrix}\vec i& \vec j&\vec k \\ 1& 2& -1\\ -2& 2& 2\end{vmatrix} =6\vec i+0\vec j+6\vec k \\(D)\times: {1\over 2}\Vert\overrightarrow{AB} \times \overrightarrow{AC} \Vert = 3\sqrt 2\ne 2\sqrt 2\\,故選\bbox[red, 2pt]{(D)}$$
解答:$$7^{10} = 1 \text{ mod }11 \Rightarrow 7^{223} =(7^{10})^{22}\cdot 7^3 =7^3 \text{ mod }11 =2\text{ mod }11 ,故選\bbox[red, 2pt]{(A)}$$
解答:$$0.\bar 3 ={3\over 9}={1\over 3},故選\bbox[red, 2pt]{(B)}$$
解答:$$\sqrt 5\approx2.236 \Rightarrow {1+\sqrt 5\over 4} \approx 0.81,故選\bbox[red, 2pt]{(C)}$$
解答:$$3f(1)+5f(1)=2+1 \Rightarrow f(1)={3\over 8}=0.375,故選\bbox[red, 2pt]{(D)}$$
解答:$$\int_0^1 {x^2\over 1+x^2}\,dx =\int_0^1 \left( 1-{1\over 1+x^2}\right)\,dx =\left. \left[ x-\tan^{-1}x\right] \right|_0^1 =1-{\pi\over 4},故選\bbox[red, 2pt]{(A)}$$
解答:$$只有四種可能\cases{1,1,2,3\\ 1,2,2,3\\ 1,2,3,3}排列數皆為{4!\over 2!}=12,因此共有12\times 3=36種,故選\bbox[red, 2pt]{(D)}$$

解答:$$假設\cases{\vec u=(2,4,3,1)\\ \vec v=(-1,-1,2,0)}\\(A)\times: (2,-1,0,0)\cdot \vec v=3\ne 0\\(B)\times:(1,1,-1,0)\cdot \vec u=3\ne 0 \\ (C)\bigcirc: \cases{ (2,0,1,-7)\cdot \vec u=0,(2,0,1,-7)\cdot \vec v=0\\ (1,-1,0,2)\cdot \vec u=0,(1,-1,0,2)\cdot \vec v=0} \\(D)\times: (0,1,-2,2)\cdot \vec v=-5\ne 0\\,故選\bbox[red, 2pt]{(C)}$$
解答:$$28人任排有28!排法,其中一半小明在小華前面,另一半小明在小華後面,因此有28!/2,故選\bbox[red, 2pt]{(D)}$$
解答:$$\cases{7= 7 \text{ mod }10 \\7^2= 9 \text{ mod }10 \\7^3= 3 \text{ mod }10 \\ 7^4= 1 \text{ mod }10 \\7^5= 7 \text{ mod }10 } \Rightarrow 循環數=4, 又\cases{7= 3 \text{ mod }4 \\7^2= 1 \text{ mod }4 \\7^3= 3 \text{ mod }4 \\7^4= 1 \text{ mod }4 } \Rightarrow 循環數2\\ 7^{7^7} =7^{3 \text{ mod }4} =3 \text{ mod }10,故選\bbox[red, 2pt]{(B)}$$
解答:$$abc=1 \Rightarrow 取a=b=c=1 \Rightarrow {1\over 1+1+1}+ {1\over 1+1+1}+ {1\over 1+1+1}=1,故選\bbox[red, 2pt]{(C)}\\\bbox[red, 2pt]{另解}\;{a\over 1+a+ab}+ {b\over 1+b+bc}+{c\over 1+c+ac} ={a\over 1+a+ab}+ {ab\over a+ab+abc}+{abc\over ab+abc+a^2bc} \\={a\over 1+a+ab}+ {ab\over a+ab+1}+{1\over ab+1+a}={a+ab+1\over 1+a+ab} =1$$
解答:$$A=\begin{bmatrix}2 & -3 & 6 \\0 & 3 & -4 \\ 0 & 2 & -3 \end{bmatrix} \Rightarrow \det(A-\lambda I)=-\lambda^3+2\lambda^2 +\lambda-2 =-(\lambda-1)(\lambda-2)(\lambda+1)=0 \\ \Rightarrow 特徵值\lambda=1,2,-1,故選\bbox[red, 2pt]{(B)}$$
解答:$$(A)x={\sqrt 2\over 4} \Rightarrow \sqrt{1-x^2} =\sqrt{7\over 8},不可能\\ (B)x={\sqrt 2\over 3} \Rightarrow \sqrt{1-x^2} =\sqrt{7\over 9},不可能\\(C)x={\sqrt 2\over 2} \Rightarrow \sqrt{1-x^2} ={\sqrt 2\over 2} \Rightarrow 2\sqrt 2\cdot {1\over 2}+{\sqrt 2\over 2}-{\sqrt 2\over 2} =\sqrt 2,符合題意\\ (D)x=\sqrt 2 \Rightarrow 1-x^2 \lt 0,不可能\\,故選\bbox[red, 2pt]{(C)}$$
解答:$$\triangle ABC :\cases{\angle C=90^\circ\\ 2\overline{BC}=\overline{AB}} \Rightarrow \cases{\angle A=30^\circ \\\angle ABC=60^\circ} \\ \Rightarrow \tan \angle DEC=\tan 60^\circ ={\overline{DC} \over \overline{EC}} \Rightarrow \sqrt 3={3\over \overline{EC}} \Rightarrow \overline{EC}=\sqrt 3,故選\bbox[red, 2pt]{(A)}$$
解答:$$\left( {\sqrt 3\over 2}-{1\over 2}i\right)^{2022} =\left( \cos{11\over 6}\pi+ i\sin {11\over 6}\pi \right)^{2022} =(e^{11\pi i/6})^{2022} =e^{11\cdot 337 \pi i} \\=e^{3707\pi i} =e^{(2 \cdot 1853+1)\pi i} =e^{\pi i} =-i,故選\bbox[red, 2pt]{(D)}$$
解答:$$\cases{A \begin{bmatrix}1 \\2\\3 \end{bmatrix} =\begin{bmatrix}1 \\1\\ 0 \end{bmatrix} \\A \begin{bmatrix}2 \\2\\4 \end{bmatrix} =\begin{bmatrix}0 \\1\\ 1 \end{bmatrix} } \Rightarrow \cases{A^{-1}\begin{bmatrix}1 \\1\\ 0 \end{bmatrix} = \begin{bmatrix}1 \\2\\3 \end{bmatrix} \\A^{-1}\begin{bmatrix}0 \\1\\ 1 \end{bmatrix} = \begin{bmatrix}2 \\2\\4 \end{bmatrix}} \Rightarrow 3A^{-1}\begin{bmatrix}1 \\1\\ 0 \end{bmatrix}-2 A^{-1}\begin{bmatrix}0 \\1\\ 1 \end{bmatrix} =3\begin{bmatrix}1 \\2\\3 \end{bmatrix}-2 \begin{bmatrix}2 \\2\\4 \end{bmatrix} \\ \Rightarrow A^{-1} \left( \begin{bmatrix}3 \\3\\ 0 \end{bmatrix}+ \begin{bmatrix}0 \\-2\\ -2 \end{bmatrix}\right) = \begin{bmatrix}3 \\6\\9 \end{bmatrix}+ \begin{bmatrix}-4 \\-4\\-8 \end{bmatrix} \Rightarrow A^{-1}\begin{bmatrix}3 \\1\\ -2 \end{bmatrix} =\begin{bmatrix}-1 \\2\\ 1 \end{bmatrix} \\ \Rightarrow A\begin{bmatrix}-1 \\2\\ 1 \end{bmatrix}= \begin{bmatrix}3 \\1\\ -2 \end{bmatrix} \Rightarrow \mathbf X=\begin{bmatrix}-1 \\2\\ 1 \end{bmatrix},故選\bbox[red, 2pt]{()}$$
解答:$$\cases{A(4,0,0) \\B(5,4,2) \\C(0,4,0) \\D(1,3,1)} \Rightarrow L=\overleftrightarrow{CD} :{x\over 1} ={y-4\over -1}={z\over 1} \Rightarrow P(t,-t+4,t),t\in \mathbb R \Rightarrow \cases{\overrightarrow{PA} =(t-4,-t+4,t) \\ \overrightarrow{PB} =(t-5,-t,t-2)}\\ \Rightarrow
\overrightarrow{PA} \cdot \overrightarrow{PB} =(t-4)(t-5)-t(-t+4)+t(t-2) =3(t-{5\over 2})^2+{5\over 4} \\ \Rightarrow 最小值={5\over 4}=1.25,故選\bbox[red, 2pt]{(B)}$$
\overrightarrow{PA} \cdot \overrightarrow{PB} =(t-4)(t-5)-t(-t+4)+t(t-2) =3(t-{5\over 2})^2+{5\over 4} \\ \Rightarrow 最小值={5\over 4}=1.25,故選\bbox[red, 2pt]{(B)}$$
解答:$$L_1\bot L_2 \Rightarrow x=4 \Rightarrow \cases{Q(2,0)\\ R(1,0)} \\ 由於\angle RPQ=90^\circ \Rightarrow \overline{QR}為外接圓直徑=2R \Rightarrow R={1\over 2}\overline{QR} ={1\over 2},故選\bbox[red, 2pt]{(D)}$$
解答:$${3+8-1\over \sqrt{3^2+4^2}} =2,故選\bbox[red, 2pt]{(D)}$$
解答:$$\sqrt{{1\over 3^2}+{1\over 4^2}+1} =\sqrt{1+({5\over 12}^2)}\\ 假設\tan \theta={5\over 12} \Rightarrow \sqrt{1+({5\over 12}^2)} =\sqrt{1+\tan^2 \theta} =\sec \theta={13\over 12} =1.08,故選\bbox[red, 2pt]{(B)}$$
解答:$$\cases{兩根之和6-m\ge 2\\ 兩根之積m-1\ge 1} \Rightarrow 2\le m\le 4 \Rightarrow \cases{m=2 \Rightarrow x^2-4x+1=0兩根非正整數\\ m=3 \Rightarrow x^2-3x+2=0\Rightarrow x=2,1},故選\bbox[red, 2pt]{(D)}$$
解答:$$(a^x+a^{-x})^2=a^{2x}+a^{-2x}+2=4 \Rightarrow a^{2x}+a^{-2x}=2\\ \Rightarrow a^{3x}+ a^{-3x} =(a^x+a^{-x})(a^{2x}-1+a^{-2x}) =2\cdot (2-1)=2,故選\bbox[red, 2pt]{(B)}$$
解答:$${1\over 2}\log{125\over 16} +\log {3\sqrt 8\over 125} -\log {3\over 5} ={1\over 2}(\log 125-\log 16) +\log 3\sqrt 8-\log 125-\log 3+\log 5 \\={3\over 2}\log 5-2\log 2+\log 3+{3\over 2} \log 2-3\log 5-\log 3+\log 5 =-{1\over 2}\log 5-{1\over 2}\log 2 \\=-{1\over 2}(1-\log 2)-{1\over 2}\log 2=-{1\over 2},故選\bbox[red, 2pt]{(A)}$$
解答:$$由於限制在區間內,因此至少有兩個極值,故選\bbox[red, 2pt]{(C)}$$
=========== END ================
解題僅供參考,教甄其他歷年試題及詳解







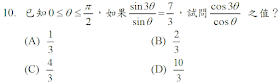

















謝謝,你的方法比較 【完備】!
回覆刪除老師您好,想請教第39題如何得知角C為90度?謝謝您
回覆刪除嚴格地講,題目並沒有標示角C是90度, 只不過這樣畫圖應該是90度吧!!?
刪除謝謝您🙂
刪除感謝提供!
回覆刪除