114 學年度中區縣市政府教師甄選策略聯盟
選擇題【共 50 題,每題 2 分,共 100 分】請以 2B 鉛筆於答案卡上作答,單選題,答錯不倒扣。
解答:$$z+{1\over z}=\sqrt 3 \Rightarrow z^2-\sqrt 3z+1=0 \Rightarrow z={\sqrt 3+i\over 2} =e^{\pi i/6} \\ \Rightarrow z^{2025} =e^{2025\pi i/6} =e^{9\pi i/6} =e^{3\pi i/2} =-i \Rightarrow z^{2025}+{1\over z^{2025}} =-i+{1\over -i}=0,故選\bbox[red, 2pt]{(C)}$$解答:$$\textbf{Case I }|2|x-2|-5|=3 \Rightarrow \cases{2|x-2|-5=3 \Rightarrow |x-2|=4 \Rightarrow \cases{x-2=4 \Rightarrow x= {\color{blue}6}\\ x-2=-4 \Rightarrow -2 \not \in \mathbb N}\\ 2|x-2|-5=-3 \Rightarrow |x-2|=1 \Rightarrow \cases{x={\color{blue}3}\\ x= {\color{blue}1}}} \\\textbf{Case II }|2|x-2|-5|=2 \Rightarrow \cases{2|x-2|-5=2 \Rightarrow |x-2|=7/2 \not \in \mathbb Z \\ 2|x-2|-5=-2 \Rightarrow |x-2|=3/2 \not \in \mathbb Z} \\\textbf{Case III } |2|x-2|-5|=1 \Rightarrow \cases{2|x-2|-5=1 \Rightarrow \cases{x= {\color{blue}5}\\ x=-1 \not \in \mathbb N}\\ 2|x-2|-5=-1 \Rightarrow |x-2|=2 \Rightarrow \cases{x= {\color{blue}4 }\\x=0 \not \in \mathbb N}} \\\textbf{Case IV }|2|x-2|-5|=0 \Rightarrow |x-2|=5/2 \not \in \mathbb Z \\\Rightarrow x=1,3,4,5,6,共五個正整數解,故選\bbox[red, 2pt]{(A)}\\公布的答案是\bbox[cyan, 2pt]{A或B}$$
解答:$$P(A\times B為偶數)=P(A為偶數)+P(B為偶數)-P(A,B皆為偶數) ={1\over 3} +{1\over 4} -{1\over 3} \cdot {1\over 4}={1\over 2} \\ P(A\times B為偶數且A\times B+C為奇數)={1\over 2}\cdot (1-{1\over 5}) ={2\over 5} \Rightarrow 條件奇數={2/5\over 1/2}={4\over 5},故選\bbox[red, 2pt]{(D)}$$
解答:$$\cases{\lim_{x\to 1} f(x) 存在 \Rightarrow 1^2-2\cdot 1=a+b \\ \lim_{x\to 4} f(x) 存在 \Rightarrow 4a+b=3\cdot 4-4=8} \Rightarrow \cases{ a+b=-1\\4a+b=8} \Rightarrow \cases{a=3\\ b=-4},故選\bbox[red, 2pt]{(C)}$$
解答:$$\cases{3的倍數有7\times 11=77個\\ 21的倍數有11個\\ 33的倍數有7個\\ 231的倍數有1個} \Rightarrow 77-11-7+1= 60,故選\bbox[red, 2pt]{(C)}$$
解答:$$3e^{xy}-x=0 \Rightarrow 3(xy'+y)e^{xy}-1=0 \Rightarrow y'= \left({1\over 3e^{xy}}-y \right)/x \Rightarrow y'(3,0) ={1\over 3}/3={1\over 9},故選\bbox[red, 2pt]{(B)}$$
解答:$$L=(1+{0.08\over n})^n \Rightarrow \ln L=n\ln(1+{0.08 \over n}) \Rightarrow \lim_{n\to \infty} \ln L= \lim_{n\to \infty} {\ln(1+{0.08 \over n})\over 1/n} \\=\lim_{n\to \infty} {(\ln(1+{0.08 \over n})) '\over (1/n)'} =\lim_{n\to \infty} {\ln(1+{0.08 \over n})\over 1/n} =\lim_{n\to \infty}{0.08n\over n+0.08} =0.08 \Rightarrow \lim_{n\to \infty}L =e^{0.08} \\ \Rightarrow \lim_{n\to \infty} 500(1+{0.08\over n})^n =500e^{0.08},故選\bbox[red, 2pt]{(A)}$$
解答:$$\int_{-3}^4 {1\over x^2+6x+12}\,dx = \int_{-3}^4 {1\over (x+3)^2+ 3}\,dx = {1\over 3}\int_{-3}^4 {1\over ({x+3\over \sqrt 3})^2+ 1}\,dx \\={1\over 3} \left. \left[\sqrt 3\tan^{-1}{x+3\over \sqrt 3} \right] \right|_{-3}^4 ={\sqrt 3\over 3}\tan^{-1}{7\over \sqrt 3},故選\bbox[red, 2pt]{(B)}$$
解答:$$(4A^T)^{-1} =\begin{bmatrix}2 & -1 \\-3 & 1\end{bmatrix} \Rightarrow 4A^T = \begin{bmatrix}2 & -1 \\-3 & 1\end{bmatrix}^{-1} =\begin{bmatrix}-1 & -1 \\-3 & -2\end{bmatrix} \Rightarrow A^T= \begin{bmatrix}-1/4 & -1/4 \\-3/4 & -2/4\end{bmatrix} \\ \Rightarrow A= \begin{bmatrix}-1/4 & -1/4 \\-3/4 & -2/4\end{bmatrix}^T =\begin{bmatrix}-1/4 & -3/4 \\-1/4 & -2/4\end{bmatrix},故選\bbox[red, 2pt]{(C)}$$
解答:$$\cases{3的倍數有7\times 11=77個\\ 21的倍數有11個\\ 33的倍數有7個\\ 231的倍數有1個} \Rightarrow 77-11-7+1= 60,故選\bbox[red, 2pt]{(C)}$$
解答:$$3e^{xy}-x=0 \Rightarrow 3(xy'+y)e^{xy}-1=0 \Rightarrow y'= \left({1\over 3e^{xy}}-y \right)/x \Rightarrow y'(3,0) ={1\over 3}/3={1\over 9},故選\bbox[red, 2pt]{(B)}$$
解答:$$L=(1+{0.08\over n})^n \Rightarrow \ln L=n\ln(1+{0.08 \over n}) \Rightarrow \lim_{n\to \infty} \ln L= \lim_{n\to \infty} {\ln(1+{0.08 \over n})\over 1/n} \\=\lim_{n\to \infty} {(\ln(1+{0.08 \over n})) '\over (1/n)'} =\lim_{n\to \infty} {\ln(1+{0.08 \over n})\over 1/n} =\lim_{n\to \infty}{0.08n\over n+0.08} =0.08 \Rightarrow \lim_{n\to \infty}L =e^{0.08} \\ \Rightarrow \lim_{n\to \infty} 500(1+{0.08\over n})^n =500e^{0.08},故選\bbox[red, 2pt]{(A)}$$
解答:$$\int_{-3}^4 {1\over x^2+6x+12}\,dx = \int_{-3}^4 {1\over (x+3)^2+ 3}\,dx = {1\over 3}\int_{-3}^4 {1\over ({x+3\over \sqrt 3})^2+ 1}\,dx \\={1\over 3} \left. \left[\sqrt 3\tan^{-1}{x+3\over \sqrt 3} \right] \right|_{-3}^4 ={\sqrt 3\over 3}\tan^{-1}{7\over \sqrt 3},故選\bbox[red, 2pt]{(B)}$$
解答:$$(4A^T)^{-1} =\begin{bmatrix}2 & -1 \\-3 & 1\end{bmatrix} \Rightarrow 4A^T = \begin{bmatrix}2 & -1 \\-3 & 1\end{bmatrix}^{-1} =\begin{bmatrix}-1 & -1 \\-3 & -2\end{bmatrix} \Rightarrow A^T= \begin{bmatrix}-1/4 & -1/4 \\-3/4 & -2/4\end{bmatrix} \\ \Rightarrow A= \begin{bmatrix}-1/4 & -1/4 \\-3/4 & -2/4\end{bmatrix}^T =\begin{bmatrix}-1/4 & -3/4 \\-1/4 & -2/4\end{bmatrix},故選\bbox[red, 2pt]{(C)}$$
解答:$$P\in L \Rightarrow P(t,6-t) \Rightarrow f(t)=|\overline{PA}-\overline{PB}|= \left| \sqrt{(t-1)^2+(2-t)^2}-\sqrt{(t-5)^2+ (4-t)^2} \right| \\= \left| {(t-1)^2+(2-6)^2-((t-5)^2+ (4-t)^2)\over\sqrt{(t-1)^2+(2-t)^2}+\sqrt{(t-5)^2+ (4-t)^2}} \right| =\left| {-12t+\cdots\over\sqrt{2t^2+\cdots}+\sqrt{2t^2+\cdots}} \right| \\ \Rightarrow \lim_{t\to \pm\infty} f(t)={12\over 2\sqrt 2} =3\sqrt 2,故選\bbox[red, 2pt]{(C)}$$
解答:$$\cases{u=\ln x \\ dv=x^2\,dx} \Rightarrow \cases{du=dx/x\\ v={1\over 3}x^3} \Rightarrow \int x^2\ln x\,dx = {1\over 3}x^3\ln x-{1\over 3}\int x^2\,dx ={1\over 3}x^3\ln x-{1\over 9}x^3+C \\ \Rightarrow \int_1^e x^2\ln x\,dx = \left. \left[ {1\over 3}x^3\ln x-{1\over 9}x^3 \right] \right|_1^e ={1\over 3}e^3-{1\over 9}e^3+{1\over 9} ={2e^3+1\over 9},故選\bbox[red, 2pt]{(C)}$$
解答:$$y=f(x)={2\over 3}(x^2+1)^{3/2 } \Rightarrow f'(x)=2x\sqrt{x^2+1}\\ \Rightarrow 弧長=\int_1^2 \sqrt{1+f'^2(x)} \,dx =\int_1^2 \sqrt{4x^4+4x^2+1} \,dx =\int_1^2 (2x^2+1)\,dx =\left. \left[{2\over 3}x^3+x \right] \right|_1^2 \\={17\over 3},故選\bbox[red, 2pt]{(B)}$$
解答:
解答:$$假設取到球的序列為X \Rightarrow \cases{P(X=黑) =2/5\\ P(X=白白黑)=(3/5)(2/4)(2/3)= 1/5\\ P(X=白白白白黑)=0} \\ \Rightarrow 甲先取到黑球的機率={2\over 5}+{1\over 5}={3\over 5},故選\bbox[red, 2pt]{(D)}$$
解答:$$25+25\times{2\over 3} +25\times{2\over 3} +25\times{2\over 3}\times{2\over 3} +25\times{2\over 3}\times{2\over 3}+\cdots \\=25(1+2\cdot {2\over 3}+ 2\cdot ({2\over 3})^2 + 2\cdot ({2\over 3})^3 + \cdots) \\=25+ {100\over 3}+50(({2\over 3})^2 + ({2\over 3})^3 + \cdots) ={175\over 3}+50\cdot {4/9\over 1-2/3} ={175\over 3}+{200\over 3}=125,故選\bbox[red, 2pt]{(D)}$$
解答:$$\lim_{x\to 2}{(x-1)^3-1\over x-2}= \lim_{x\to 2}{((x-1)^3-1)'\over (x-2)'} =\lim_{x\to 2}{3(x-1)^2\over 1} =3,故選\bbox[red, 2pt]{(D)}$$

解答:$$f(x)=(x-b)(x-c)p(x)+2x+1= (x-a)(x-c)q(x)-x+7 = (x-a)(x-b)r(x)+3x-5 \\ \Rightarrow \cases{f(a)=-a+7=3a-5\\ f(b)=2b+1 =3b-5\\ f(c)=2c+1=-c+7} \Rightarrow \cases{a=3\\ b=6 \\c=2} \Rightarrow a+b+c=11,故選\bbox[red, 2pt]{(D)}$$
解答:$$\cases{u=\ln x \\ dv=x^2\,dx} \Rightarrow \cases{du=dx/x\\ v={1\over 3}x^3} \Rightarrow \int x^2\ln x\,dx = {1\over 3}x^3\ln x-{1\over 3}\int x^2\,dx ={1\over 3}x^3\ln x-{1\over 9}x^3+C \\ \Rightarrow \int_1^e x^2\ln x\,dx = \left. \left[ {1\over 3}x^3\ln x-{1\over 9}x^3 \right] \right|_1^e ={1\over 3}e^3-{1\over 9}e^3+{1\over 9} ={2e^3+1\over 9},故選\bbox[red, 2pt]{(C)}$$
解答:$$y=f(x)={2\over 3}(x^2+1)^{3/2 } \Rightarrow f'(x)=2x\sqrt{x^2+1}\\ \Rightarrow 弧長=\int_1^2 \sqrt{1+f'^2(x)} \,dx =\int_1^2 \sqrt{4x^4+4x^2+1} \,dx =\int_1^2 (2x^2+1)\,dx =\left. \left[{2\over 3}x^3+x \right] \right|_1^2 \\={17\over 3},故選\bbox[red, 2pt]{(B)}$$
解答:
$$半圓面積+矩形面積={1\over 2}\cdot 8^2\pi+ 16\cdot 3=32\pi +48,故選\bbox[red, 2pt]{(C)}$$
解答:$$(D)\times: A行向量線性相依\Rightarrow \det(A)=0 \Rightarrow A^{-1}不存在,故選\bbox[red, 2pt]{(D)}$$
解答:$$A= \left[ \begin{matrix}1 & 2 & 3 & 4\\2 & 4 & 6 & 8\\0 & 1 & 1 & 1\\1 & 3 & 4 & 5\end{matrix} \right] \xrightarrow{R_2-2R_1\to R_2, R_4-R_1\to R_4}\begin{bmatrix} 1 & 2 & 3 & 4\\0 & 0 & 0 & 0\\0 & 1 & 1 & 1\\0 & 1 & 1 & 1 \end{bmatrix} \xrightarrow{R_3-R_4\to R_3} \begin{bmatrix} 1 & 2 & 3 & 4\\0 & 0 & 0 & 0\\0 & 0 & 0 & 0\\0 & 1 & 1 & 1\end{bmatrix}\\ \xrightarrow{R_1-2R_4} \begin{bmatrix} 1 & 0 & 1 & 2\\0 & 0 & 0 & 0\\0 & 0 & 0 & 0\\0 & 1 & 1 & 1\end{bmatrix} \xrightarrow{R_2\leftrightarrow R_4} \begin{bmatrix} 1 & 0 & 1 & 2\\0 & 1 & 1 & 1\\0 & 0 & 0 & 0\\0 & 0 & 0 & 0\end{bmatrix} \\ \Rightarrow rref(A) =\begin{bmatrix} 1 & 0 & 1 & 2\\0 & 1 & 1 & 1\\0 & 0 & 0 & 0\\0 & 0 & 0 & 0\end{bmatrix} \Rightarrow rank(A)=2,故選\bbox[red, 2pt]{(B)}$$
解答:$${dy\over dx}=3y \Rightarrow {1\over y}dy =3\,dx \Rightarrow \int {1\over y}dy =\int 3\,dx \Rightarrow \ln y=3x+C_1 \Rightarrow y=e^{3x+C_1} =C e^{3x},故選\bbox[red, 2pt]{(B)}$$
解答:$$假設a=10,b=100\\(A)\times: \cases{\log a=1\\ \log b=2} \Rightarrow \log a\not \gt \log b\\ (B)\times: x=1 \Rightarrow \log_a x=0=\log_b x\\ (C)\times: x=10 \Rightarrow \cases{\log_a x=1\\ \log_b x=1/2} \Rightarrow \log_b x\not \gt \log_a x\\,故選\bbox[red, 2pt]{(D)}$$
解答:$$直線L:5x+4y=k \Rightarrow 斜率為-{5\over 4}\\橢圓:4x^2+(y-1)^2=4 \Rightarrow 8x+2(y-1)y'=0 \Rightarrow y'=-{8x\over 2(y-1)} =-{4x\over y-1}=-{5\over 4} \Rightarrow 16x=5y-5 \\ \Rightarrow y={16x+5\over 5} 代入橢圓\Rightarrow 4x^2+({16x\over 5})^2=4 \Rightarrow x^2={25\over 89} \Rightarrow x={5\over \sqrt{89}} \\ \Rightarrow 5x+4y=5x+ {64x+20\over 5}={25\over \sqrt{89}}+{64\over \sqrt{89}}+4= 4+\sqrt{89} \approx 4+9=13,故選\bbox[red, 2pt]{(C)}$$
解答:$$\cases{\vec a=(1,-1,2) \\\vec b=(3,4,-1)} \Rightarrow \cases{-2b=(-6,-8,2) \\ 2a+b=(5,2,3)} \Rightarrow \cos \theta ={(-6,-8,2) \cdot (5,2,3) \over |(-6,-8,2)||(5,-3,3)} \lt 0 \Rightarrow \theta \gt 90^\circ \ne 70^\circ\\,故選\bbox[red, 2pt]{(C)}$$
解答:$$\begin{vmatrix}1& x+1& 3x-1\\ x& x-2& x-3\\ x-1& x+1& x-1 \end{vmatrix} =9x^2-11x+10\\ (A)\times: 常數項為10\ne 11\\ (B)\bigcirc: 9-11+10=8\\ (C)\times :奇次項係數和=-11 \ne 4\\ (D)\times: 偶次項係數和=9+10=19 \ne 5,故選\bbox[red, 2pt]{(B)}$$
解答:$$X\sim B(n=2,p=1/6) \Rightarrow E(X)=np ={1\over 3},故選\bbox[red, 2pt]{(D)}$$
解答:$$(D)\times: A行向量線性相依\Rightarrow \det(A)=0 \Rightarrow A^{-1}不存在,故選\bbox[red, 2pt]{(D)}$$
解答:$$A= \left[ \begin{matrix}1 & 2 & 3 & 4\\2 & 4 & 6 & 8\\0 & 1 & 1 & 1\\1 & 3 & 4 & 5\end{matrix} \right] \xrightarrow{R_2-2R_1\to R_2, R_4-R_1\to R_4}\begin{bmatrix} 1 & 2 & 3 & 4\\0 & 0 & 0 & 0\\0 & 1 & 1 & 1\\0 & 1 & 1 & 1 \end{bmatrix} \xrightarrow{R_3-R_4\to R_3} \begin{bmatrix} 1 & 2 & 3 & 4\\0 & 0 & 0 & 0\\0 & 0 & 0 & 0\\0 & 1 & 1 & 1\end{bmatrix}\\ \xrightarrow{R_1-2R_4} \begin{bmatrix} 1 & 0 & 1 & 2\\0 & 0 & 0 & 0\\0 & 0 & 0 & 0\\0 & 1 & 1 & 1\end{bmatrix} \xrightarrow{R_2\leftrightarrow R_4} \begin{bmatrix} 1 & 0 & 1 & 2\\0 & 1 & 1 & 1\\0 & 0 & 0 & 0\\0 & 0 & 0 & 0\end{bmatrix} \\ \Rightarrow rref(A) =\begin{bmatrix} 1 & 0 & 1 & 2\\0 & 1 & 1 & 1\\0 & 0 & 0 & 0\\0 & 0 & 0 & 0\end{bmatrix} \Rightarrow rank(A)=2,故選\bbox[red, 2pt]{(B)}$$
解答:$${dy\over dx}=3y \Rightarrow {1\over y}dy =3\,dx \Rightarrow \int {1\over y}dy =\int 3\,dx \Rightarrow \ln y=3x+C_1 \Rightarrow y=e^{3x+C_1} =C e^{3x},故選\bbox[red, 2pt]{(B)}$$
解答:$$假設a=10,b=100\\(A)\times: \cases{\log a=1\\ \log b=2} \Rightarrow \log a\not \gt \log b\\ (B)\times: x=1 \Rightarrow \log_a x=0=\log_b x\\ (C)\times: x=10 \Rightarrow \cases{\log_a x=1\\ \log_b x=1/2} \Rightarrow \log_b x\not \gt \log_a x\\,故選\bbox[red, 2pt]{(D)}$$
解答:$$直線L:5x+4y=k \Rightarrow 斜率為-{5\over 4}\\橢圓:4x^2+(y-1)^2=4 \Rightarrow 8x+2(y-1)y'=0 \Rightarrow y'=-{8x\over 2(y-1)} =-{4x\over y-1}=-{5\over 4} \Rightarrow 16x=5y-5 \\ \Rightarrow y={16x+5\over 5} 代入橢圓\Rightarrow 4x^2+({16x\over 5})^2=4 \Rightarrow x^2={25\over 89} \Rightarrow x={5\over \sqrt{89}} \\ \Rightarrow 5x+4y=5x+ {64x+20\over 5}={25\over \sqrt{89}}+{64\over \sqrt{89}}+4= 4+\sqrt{89} \approx 4+9=13,故選\bbox[red, 2pt]{(C)}$$
解答:$$\cases{\vec a=(1,-1,2) \\\vec b=(3,4,-1)} \Rightarrow \cases{-2b=(-6,-8,2) \\ 2a+b=(5,2,3)} \Rightarrow \cos \theta ={(-6,-8,2) \cdot (5,2,3) \over |(-6,-8,2)||(5,-3,3)} \lt 0 \Rightarrow \theta \gt 90^\circ \ne 70^\circ\\,故選\bbox[red, 2pt]{(C)}$$
解答:$$\begin{vmatrix}1& x+1& 3x-1\\ x& x-2& x-3\\ x-1& x+1& x-1 \end{vmatrix} =9x^2-11x+10\\ (A)\times: 常數項為10\ne 11\\ (B)\bigcirc: 9-11+10=8\\ (C)\times :奇次項係數和=-11 \ne 4\\ (D)\times: 偶次項係數和=9+10=19 \ne 5,故選\bbox[red, 2pt]{(B)}$$
解答:$$X\sim B(n=2,p=1/6) \Rightarrow E(X)=np ={1\over 3},故選\bbox[red, 2pt]{(D)}$$
解答:$$假設取到球的序列為X \Rightarrow \cases{P(X=黑) =2/5\\ P(X=白白黑)=(3/5)(2/4)(2/3)= 1/5\\ P(X=白白白白黑)=0} \\ \Rightarrow 甲先取到黑球的機率={2\over 5}+{1\over 5}={3\over 5},故選\bbox[red, 2pt]{(D)}$$
解答:$$25+25\times{2\over 3} +25\times{2\over 3} +25\times{2\over 3}\times{2\over 3} +25\times{2\over 3}\times{2\over 3}+\cdots \\=25(1+2\cdot {2\over 3}+ 2\cdot ({2\over 3})^2 + 2\cdot ({2\over 3})^3 + \cdots) \\=25+ {100\over 3}+50(({2\over 3})^2 + ({2\over 3})^3 + \cdots) ={175\over 3}+50\cdot {4/9\over 1-2/3} ={175\over 3}+{200\over 3}=125,故選\bbox[red, 2pt]{(D)}$$
解答:$$\lim_{x\to 2}{(x-1)^3-1\over x-2}= \lim_{x\to 2}{((x-1)^3-1)'\over (x-2)'} =\lim_{x\to 2}{3(x-1)^2\over 1} =3,故選\bbox[red, 2pt]{(D)}$$
解答:$$f(x)=x^3+ax^2+bx+c \Rightarrow f'(x)=3x^2+2ax+b \\ \cases{x=-1有極大值2\\ x=3有極小值} \Rightarrow \cases{f(-1)=2\\ f'(-1)=0\\ f'(3) =0} \Rightarrow \cases{-1+a-b+c=2\\3-2a+b=0\\ 27+6a+b=0} \Rightarrow \cases{a=-3\\ b=-9\\ c=-3} \\ \Rightarrow a+b+c=-15,故選\bbox[red, 2pt]{(B)}$$
解答:$$\int_0^4(1-\sqrt{16-x^2}) \,dx = \int_0^4 1\,dx - \int_0^4 \sqrt{16-x^2}\,dx =4-4\pi(四分之一圓),故選\bbox[red, 2pt]{(C)}$$
解答:$$P(A')={1\over 4} \Rightarrow P(A)={3\over 4}, 又P(A'\cup B)={1\over 2} \Rightarrow P(A\cap B)={3\over 4}-{1\over 2}={1\over 4} \\ \Rightarrow P(B\mid A)={P(A\cap B)\over P(A)} ={1/4\over 3/4} ={1\over 3},故選\bbox[red, 2pt]{(C)}$$
解答:$$\int_0^4(1-\sqrt{16-x^2}) \,dx = \int_0^4 1\,dx - \int_0^4 \sqrt{16-x^2}\,dx =4-4\pi(四分之一圓),故選\bbox[red, 2pt]{(C)}$$
解答:$$P(A')={1\over 4} \Rightarrow P(A)={3\over 4}, 又P(A'\cup B)={1\over 2} \Rightarrow P(A\cap B)={3\over 4}-{1\over 2}={1\over 4} \\ \Rightarrow P(B\mid A)={P(A\cap B)\over P(A)} ={1/4\over 3/4} ={1\over 3},故選\bbox[red, 2pt]{(C)}$$
$$R=四分之一圓, 繞y軸旋轉得一半球, 半球體積={4\over 3}\pi\cdot 2^3\times {1\over 2}={16\over 3}\pi,故選\bbox[red, 2pt]{(B)}$$
解答:
解答:
$$由電腦繪圖可知最大值小於二分之一,但公佈的答案是\bbox[cyan,2pt]{(C)}, 試題有疑義!!$$
解答:$$f(x)=\sqrt{1+\sqrt{x+8}}-2 \Rightarrow f'(x)={1\over 4}(1+(x+8)^{-1/2})^{-1/2}(x+8)^{-1/2} \Rightarrow f'(1)= {1\over 4}\cdot {1\over 2}\cdot {1\over 3}={1\over 24} \\ \Rightarrow \lim_{x\to 1}{f(x)\over x-1} = \lim_{x\to 1}{f'(x)\over (x-1)'} =f'(1)={1\over 24},故選\bbox[red, 2pt]{(B)}$$
解答:$$x={\sqrt 3+1\over 2\sqrt 2}+{\sqrt 3-1\over 2\sqrt 2}i \Rightarrow x^2={4+2\sqrt 3\over 8} +{2\over 4}i-{ 4-2\sqrt 3\over 8} ={\sqrt 3\over 2}+{1\over 2}i =\cos 30^\circ +i\sin 30^\circ \\ \Rightarrow z=(\cos 30^\circ+i\sin 30)^3= \cos 90^\circ +i\sin 90^\circ =i,故選\bbox[red, 2pt]{(C)}$$
解答:$$信賴區間=[\bar x-d,\bar x+d] \Rightarrow 寬度=2d與平均值\bar x無關,故選\bbox[red, 2pt]{(B)}$$
解答:$$\cases{f(x)=x+2\\ g(x)=ax-2} \Rightarrow \cases{f(g(x))=f(ax-2)=ax\\ g(f(x)) =g(x+2)=ax+2a-2} \Rightarrow f(g(x))=g(f(x)) \Rightarrow 2a-2=0 \\ \Rightarrow a=1,故選\bbox[red, 2pt]{(A)}$$
解答:$$f(x)=\sqrt{1+\sqrt{x+8}}-2 \Rightarrow f'(x)={1\over 4}(1+(x+8)^{-1/2})^{-1/2}(x+8)^{-1/2} \Rightarrow f'(1)= {1\over 4}\cdot {1\over 2}\cdot {1\over 3}={1\over 24} \\ \Rightarrow \lim_{x\to 1}{f(x)\over x-1} = \lim_{x\to 1}{f'(x)\over (x-1)'} =f'(1)={1\over 24},故選\bbox[red, 2pt]{(B)}$$
解答:$$x={\sqrt 3+1\over 2\sqrt 2}+{\sqrt 3-1\over 2\sqrt 2}i \Rightarrow x^2={4+2\sqrt 3\over 8} +{2\over 4}i-{ 4-2\sqrt 3\over 8} ={\sqrt 3\over 2}+{1\over 2}i =\cos 30^\circ +i\sin 30^\circ \\ \Rightarrow z=(\cos 30^\circ+i\sin 30)^3= \cos 90^\circ +i\sin 90^\circ =i,故選\bbox[red, 2pt]{(C)}$$
解答:$$信賴區間=[\bar x-d,\bar x+d] \Rightarrow 寬度=2d與平均值\bar x無關,故選\bbox[red, 2pt]{(B)}$$
解答:$$\cases{f(x)=x+2\\ g(x)=ax-2} \Rightarrow \cases{f(g(x))=f(ax-2)=ax\\ g(f(x)) =g(x+2)=ax+2a-2} \Rightarrow f(g(x))=g(f(x)) \Rightarrow 2a-2=0 \\ \Rightarrow a=1,故選\bbox[red, 2pt]{(A)}$$
解答:$$(A)\times: \cases{a=b=11\\ c=10} \Rightarrow s=(a+b+c)/2 =16 \Rightarrow \sqrt{16\cdot 5\cdot 5\cdot 6} \not \in \mathbb N \\(B) \times: \cases{a=b=12\\ c=10} \Rightarrow s=(a+b+c)/2 =17 \Rightarrow \sqrt{17\cdot 5\cdot 5\cdot 7} \not \in \mathbb N \\(C)\bigcirc: \cases{a=b=13\\ c=10} \Rightarrow s=(a+b+c)/2 =18 \Rightarrow \sqrt{18\cdot 5\cdot 5\cdot 8} =60 \\(D)\bigcirc: \cases{a=b=14\\ c=10} \Rightarrow s=(a+b+c)/2 =19 \Rightarrow \sqrt{19\cdot 5\cdot 5\cdot 9} \not \in \mathbb N \\,故選\bbox[red, 2pt]{(C)}$$
解答:$$f(x,y)=x^2+y^2 +(x-2y+6)^2 \Rightarrow \cases{f_x=2x+2(x-2y+6) =0\\ f_y=2y-4(x-2y+6) =0} \Rightarrow \cases{ x=-1\\ y=2} \\ \Rightarrow f(-1,2)=1+4+(-1-4+6)^2=6,故選\bbox[red, 2pt]{(B)}$$
解答:$$f(x,y)=x^2+y^2 +(x-2y+6)^2 \Rightarrow \cases{f_x=2x+2(x-2y+6) =0\\ f_y=2y-4(x-2y+6) =0} \Rightarrow \cases{ x=-1\\ y=2} \\ \Rightarrow f(-1,2)=1+4+(-1-4+6)^2=6,故選\bbox[red, 2pt]{(B)}$$

解答:$$f(x)=(x-b)(x-c)p(x)+2x+1= (x-a)(x-c)q(x)-x+7 = (x-a)(x-b)r(x)+3x-5 \\ \Rightarrow \cases{f(a)=-a+7=3a-5\\ f(b)=2b+1 =3b-5\\ f(c)=2c+1=-c+7} \Rightarrow \cases{a=3\\ b=6 \\c=2} \Rightarrow a+b+c=11,故選\bbox[red, 2pt]{(D)}$$
$$x^2+y^2-4x-6y+4=0 \Rightarrow (x-2)^2+ (y-3)^2=9 \Rightarrow 圓心O(2,3)\\ 假設過A之弦中點為P(x,y), 則\angle OPA=90^\circ \Rightarrow \overline{OA}^2=\overline{PO}^2+\overline{PA}^2 \\ \Rightarrow 8=(x-2)^2+(y-3)^2+(x-4)^2+(y-5)^2 =2x^2+2y^2-12x-16y+54 \\ \Rightarrow x^2+y^2-6x-8y+23=0 \Rightarrow (x-3)^2+(y-4)^2=2 \Rightarrow 圓心為(3,4),故選\bbox[red, 2pt]{(A)}$$
解答:$$題目應該加一句:\cases{\overline{BC}=a\\ \overline{AC}=b\\ \overline{AB} =c}, (a+b+c)(a+b-c)=a^2+b^2-c^2+2ab=ab \\ \Rightarrow a^2+b^2-c^2=-ab \Rightarrow \cos \angle C={a^2+b^2-c^2\over 2ab}={-ab\over 2ab}=-{1\over 2} \Rightarrow \angle C=120^\circ,故選\bbox[red, 2pt]{(C)}$$
解答:$$f(x)=4^{x+1}-2^{x+1} \Rightarrow f'(x)=\ln 4\cdot 4^{x+1}-\ln 2\cdot 2^{x+1} =2\ln 2\cdot 2^{2x+2}-\ln2\cdot 2^{x+1}= \ln 2(2^{2x+3}-2^{x+1}) \\ 因此f'(x)=0 \Rightarrow 2x+3=x+1 \Rightarrow x=-2, 又f'(x)\gt 0, \text{ for }x\gt -2 \Rightarrow f(x)遞增,x\gt -2\\ 因此在區間-2\le x\le 2, \cases{M=f(2)=4^3-2^3=56\\ m=f(-2)=4^{-1}-2^{-1}=-1/4} \Rightarrow M+m={223\over 4},故選\bbox[red, 2pt]{(A)}$$
解答:$$S={1\over 2}+{3\over 2^2}+{5\over 2^3}+ \cdots +{15\over 2^8}+{17\over 2^9} \Rightarrow {1\over 2}S={1\over 2^2}+{3\over 2^3}+{5\over 2^4}+ \cdots +{15\over 2^9}+{17\over 2^{10}} \\ \Rightarrow S-{1\over 2}S= {1\over 2}+{2\over 2^2}+{2\over 2^3} + \cdots +{2\over 2^9}-{17\over 2^{10}} \Rightarrow {1\over 2}S={1\over 2}+{1\over 2}+{1\over 2^2}+ \cdots+{1\over 2^8}-{17\over 2^{10}} \\ \Rightarrow S=1+1+{1\over 2}+{1\over 2^2}+\cdots+{1\over 2^7}-{17\over 2^9}=1+{255\over 128}-{17\over 512} ={1515\over 512},故選\bbox[red, 2pt]{(B)}$$
解答:$$C^{12}_5C^7_4C^3_3 =166320,故選\bbox[red, 2pt]{(D)}$$
解答:$$令\cases{f(x)=(x^2+3x+2)^{10} \\g(x)=x^2+2x+3} \Rightarrow f(x) =(x^4+6x^3 +13x^2+12x+4)^5 =((x^2+4x+12)g(x)-4x-2)^5 \\ \Rightarrow 只需考慮(-4x-2)^5除以g(x)的餘式\\ 又(-4x-2)^5=(-64x^3-96x^2-48x-8)(16x^2+16x+4) \\=((-64x+32)g(x)+80x-104)(16g(x)-16x-44) \Rightarrow 只需考慮(80x-104)(-16x-44) \\又(80x-104)(-16x-44)=-1280x^2-1856x+4576=-1280g(x)+704x+8416 \\ \Rightarrow 704x+8416,故選\bbox[red, 2pt]{(A)}$$
解答:$$e^1=e \Rightarrow \ln(e)=1,故選\bbox[red, 2pt]{(C)}$$
解答:$$\lim_{x\to \infty}{4x-\sin(x^2+5x+7) \over x-\cos(2x-3)} =\lim_{x\to \infty}{4x \over x } =4,故選\bbox[red, 2pt]{(D)}$$
解答:$$f(x)=(4x^2+3) (5x+3)^2 \Rightarrow f'(x)=8x(5x+3)^2 +10(4x^2+3)(5x+3) \Rightarrow f'(1)=8^3+10\cdot 7\cdot 8 \\=1072,故選\bbox[red, 2pt]{(D)}$$
解答:$$\int_0^\pi \cos^2(x)\,dx = {1\over 2}\int_0^\pi (\cos(2x)+1)\,dx ={1\over 2}\left. \left[ {1\over 2}\sin(2x)+x \right] \right|_0^\pi ={\pi\over 2},故選\bbox[red, 2pt]{(A)}$$
解答:$$1-{1\over 3}+{1\over 5}-{1\over 7}+{1\over 9}- \cdots \\= \left. \left[x-{1\over 3}x^3 +{1\over 5}x^5 -{1\over 7}x^7+{1\over 9}x^9-\cdots\right] \right|_0^1 =\int_0^1 (1-x^2+x^4-x^6+x^8+\cdots)\,dx \\=\int_0^1 {1\over 1+x^2}\,dx = \left. \left[ \tan^{-1} x \right] \right|_0^1 ={\pi\over 4},故選\bbox[red, 2pt]{(B)}$$
解答:$$f(x,y)=x^4+y^4-4xy+8 \Rightarrow \cases{f_x=4x^3-4y\\ f_y=4y^3-4x} \Rightarrow \cases{f_{xx}= 12x^2\\ f_{xy}= -4\\ f_{yy} =12y^2} \Rightarrow d(x,y)=f_{xx}f_{yy}-(f_{xy})^2 \\ \Rightarrow d(x,y)=144x^2y^2-16 \\ 若\cases{f_x=0\\ f_y=0} \Rightarrow \cases{x^3=y\\ y^3=x} \Rightarrow y^9=y \Rightarrow y(y^8-1)=0 \Rightarrow \cases{y=0 \Rightarrow x=0\\ y=1 \Rightarrow x=1\\ y=-1\Rightarrow x=-1} \\\Rightarrow (0,0),(1,1),(-1,-1) 為臨界點 又\cases{d(0,0)=-16\lt 0\Rightarrow (0,0)為鞍點 \\ d(1,1)=128\gt 0 \Rightarrow f_{xx}(1,1) \gt 0 \Rightarrow f(1,1)為極小值\\ d(-1,-1)=128\gt 0 \Rightarrow f_{xx}(-1,-1)=\gt 0 \Rightarrow f(-1,-1)為極小值}\\,故選\bbox[red, 2pt]{(D)}$$
解答:$$\det(A ) = 16+140+162- 126-192-15=-15,故選\bbox[red, 2pt]{(A)}$$
解答:$$\det(A-\lambda I) =-\lambda^3+9 \lambda^2-26\lambda+24 =-(\lambda-2) (\lambda-3)(\lambda-4) \Rightarrow 特徵值\lambda=2,3,4,故選\bbox[red, 2pt]{(A)}$$

====================== END ==========================
解題僅供參考,其他教甄試題及詳解
解答:$$題目應該加一句:\cases{\overline{BC}=a\\ \overline{AC}=b\\ \overline{AB} =c}, (a+b+c)(a+b-c)=a^2+b^2-c^2+2ab=ab \\ \Rightarrow a^2+b^2-c^2=-ab \Rightarrow \cos \angle C={a^2+b^2-c^2\over 2ab}={-ab\over 2ab}=-{1\over 2} \Rightarrow \angle C=120^\circ,故選\bbox[red, 2pt]{(C)}$$
解答:$$f(x)=4^{x+1}-2^{x+1} \Rightarrow f'(x)=\ln 4\cdot 4^{x+1}-\ln 2\cdot 2^{x+1} =2\ln 2\cdot 2^{2x+2}-\ln2\cdot 2^{x+1}= \ln 2(2^{2x+3}-2^{x+1}) \\ 因此f'(x)=0 \Rightarrow 2x+3=x+1 \Rightarrow x=-2, 又f'(x)\gt 0, \text{ for }x\gt -2 \Rightarrow f(x)遞增,x\gt -2\\ 因此在區間-2\le x\le 2, \cases{M=f(2)=4^3-2^3=56\\ m=f(-2)=4^{-1}-2^{-1}=-1/4} \Rightarrow M+m={223\over 4},故選\bbox[red, 2pt]{(A)}$$
解答:$$S={1\over 2}+{3\over 2^2}+{5\over 2^3}+ \cdots +{15\over 2^8}+{17\over 2^9} \Rightarrow {1\over 2}S={1\over 2^2}+{3\over 2^3}+{5\over 2^4}+ \cdots +{15\over 2^9}+{17\over 2^{10}} \\ \Rightarrow S-{1\over 2}S= {1\over 2}+{2\over 2^2}+{2\over 2^3} + \cdots +{2\over 2^9}-{17\over 2^{10}} \Rightarrow {1\over 2}S={1\over 2}+{1\over 2}+{1\over 2^2}+ \cdots+{1\over 2^8}-{17\over 2^{10}} \\ \Rightarrow S=1+1+{1\over 2}+{1\over 2^2}+\cdots+{1\over 2^7}-{17\over 2^9}=1+{255\over 128}-{17\over 512} ={1515\over 512},故選\bbox[red, 2pt]{(B)}$$
解答:$$C^{12}_5C^7_4C^3_3 =166320,故選\bbox[red, 2pt]{(D)}$$
解答:$$令\cases{f(x)=(x^2+3x+2)^{10} \\g(x)=x^2+2x+3} \Rightarrow f(x) =(x^4+6x^3 +13x^2+12x+4)^5 =((x^2+4x+12)g(x)-4x-2)^5 \\ \Rightarrow 只需考慮(-4x-2)^5除以g(x)的餘式\\ 又(-4x-2)^5=(-64x^3-96x^2-48x-8)(16x^2+16x+4) \\=((-64x+32)g(x)+80x-104)(16g(x)-16x-44) \Rightarrow 只需考慮(80x-104)(-16x-44) \\又(80x-104)(-16x-44)=-1280x^2-1856x+4576=-1280g(x)+704x+8416 \\ \Rightarrow 704x+8416,故選\bbox[red, 2pt]{(A)}$$
解答:$$e^1=e \Rightarrow \ln(e)=1,故選\bbox[red, 2pt]{(C)}$$
解答:$$\lim_{x\to \infty}{4x-\sin(x^2+5x+7) \over x-\cos(2x-3)} =\lim_{x\to \infty}{4x \over x } =4,故選\bbox[red, 2pt]{(D)}$$
解答:$$f(x)=(4x^2+3) (5x+3)^2 \Rightarrow f'(x)=8x(5x+3)^2 +10(4x^2+3)(5x+3) \Rightarrow f'(1)=8^3+10\cdot 7\cdot 8 \\=1072,故選\bbox[red, 2pt]{(D)}$$
解答:$$\int_0^\pi \cos^2(x)\,dx = {1\over 2}\int_0^\pi (\cos(2x)+1)\,dx ={1\over 2}\left. \left[ {1\over 2}\sin(2x)+x \right] \right|_0^\pi ={\pi\over 2},故選\bbox[red, 2pt]{(A)}$$
解答:$$1-{1\over 3}+{1\over 5}-{1\over 7}+{1\over 9}- \cdots \\= \left. \left[x-{1\over 3}x^3 +{1\over 5}x^5 -{1\over 7}x^7+{1\over 9}x^9-\cdots\right] \right|_0^1 =\int_0^1 (1-x^2+x^4-x^6+x^8+\cdots)\,dx \\=\int_0^1 {1\over 1+x^2}\,dx = \left. \left[ \tan^{-1} x \right] \right|_0^1 ={\pi\over 4},故選\bbox[red, 2pt]{(B)}$$
解答:$$f(x,y)=x^4+y^4-4xy+8 \Rightarrow \cases{f_x=4x^3-4y\\ f_y=4y^3-4x} \Rightarrow \cases{f_{xx}= 12x^2\\ f_{xy}= -4\\ f_{yy} =12y^2} \Rightarrow d(x,y)=f_{xx}f_{yy}-(f_{xy})^2 \\ \Rightarrow d(x,y)=144x^2y^2-16 \\ 若\cases{f_x=0\\ f_y=0} \Rightarrow \cases{x^3=y\\ y^3=x} \Rightarrow y^9=y \Rightarrow y(y^8-1)=0 \Rightarrow \cases{y=0 \Rightarrow x=0\\ y=1 \Rightarrow x=1\\ y=-1\Rightarrow x=-1} \\\Rightarrow (0,0),(1,1),(-1,-1) 為臨界點 又\cases{d(0,0)=-16\lt 0\Rightarrow (0,0)為鞍點 \\ d(1,1)=128\gt 0 \Rightarrow f_{xx}(1,1) \gt 0 \Rightarrow f(1,1)為極小值\\ d(-1,-1)=128\gt 0 \Rightarrow f_{xx}(-1,-1)=\gt 0 \Rightarrow f(-1,-1)為極小值}\\,故選\bbox[red, 2pt]{(D)}$$
解答:$$\det(A ) = 16+140+162- 126-192-15=-15,故選\bbox[red, 2pt]{(A)}$$
解答:$$\det(A-\lambda I) =-\lambda^3+9 \lambda^2-26\lambda+24 =-(\lambda-2) (\lambda-3)(\lambda-4) \Rightarrow 特徵值\lambda=2,3,4,故選\bbox[red, 2pt]{(A)}$$

解題僅供參考,其他教甄試題及詳解













































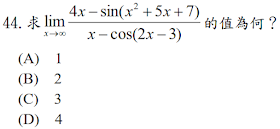






第29題在古早簡體數競賽數看到,裏面胡說八道,真實狀況應該答案小於1。為何不送分,很難懂。
回覆刪除