解:
此題相當於求以下聯立方程式:
一般而言式(3)為一圓方程式,而式(2)為一直線,兩者相交恰有一實數解表示相交於圓切點上。也就是將式(2)代入式(3)可得
由求得的k值,可得此圓的兩條切線為y=2x ±√5,如下圖
但由式(1)可知:y≥0 ⇔ (1-x2)≥0,也就是說式(3)的圓僅有上半部。而直線與半圓大部份相交於一點,僅有少部份情況是相交兩點。
若直線y=2x+k經過半圓的左右兩端點(1,0)、(-1,0),可求得k=-2及k=2,如下圖的兩條藍線。
介於兩條藍線間的所有直線均與半圓相交一點(除了k=2時剛好交於兩點),介於紅色切線於左邊藍線的直線均與半圓相交兩點(除了k=√5時剛好交於一點)。
因此直線y=2x+k與半圓交於一點的條件為:
k=√5及-2≤k<2
-- END --


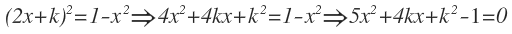



沒有留言:
張貼留言