國中數學：常見的平行與比例問題

國中數學中，有幾個常見的平行求比例的問題，相互之間有關聯且容易搞混，特地再寫一遍。

常見一

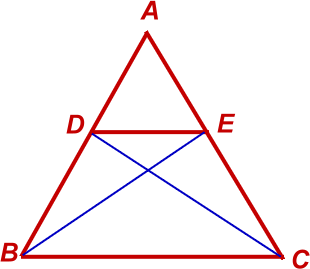
$$\triangle ABC中，\overline { DE } //\overline { BC } (如上圖)\Rightarrow \frac { \overline { AD }  }{ \overline { DB }  } =\frac { \overline { AE }  }{ \overline { EC }  } $$

解：

$$由於\overline { DE } //\overline { BC } \Rightarrow 面積\triangle DEB=\frac { 1 }{ 2 } \times \overline { DE } \times \left( \overline { DE } 與\overline { BC } 的距離 \right) =面積\triangle DEC$$$$因此\frac { \overline { AD }  }{ \overline { DB }  } =\frac { \triangle ADE }{ \triangle DEB } =\frac { \triangle ADE }{ \triangle DEC } =\frac { \overline { AE }  }{ \overline { EC }  } \Rightarrow \frac { \overline { AD }  }{ \overline { DB }  } =\frac { \overline { AE }  }{ \overline { EC }  }  $$

---

常見二

$$若\overline { AD } //\overline { BE } //\overline { CF } ，如上圖，則\frac { \overline { AB }  }{ \overline { BC }  } =\frac { \overline { DE }  }{ \overline { EF }  } $$
解：

$$\begin{cases} 在\triangle CDA中,\frac { \overline { BC }  }{ \overline { AB }  } =\frac { \overline { CG }  }{ \overline { GD }  }  \\ 在\triangle DCF中,\frac { \overline { DG }  }{ \overline { GC }  } =\frac { \overline { DE }  }{ \overline { EF }  }  \end{cases}\Rightarrow \frac { \overline { AB }  }{ \overline { BC }  } =\frac { \overline { DG }  }{ \overline { GC }  } =\frac { \overline { DE }  }{ \overline { EF }  } $$

---

常見三

$$在\triangle ABC中,\overline { AD } 為\angle A的角平分線,則\frac { \overline { AB }  }{ \overline { AC }  } =\frac { \overline { BD }  }{ \overline { DC }  } $$
解：

在\(\overline{BA}\)延長線上找一點E，使得\(\overline{DA}//\overline{CE}\)，如上圖。
$$由於\overline { DA } //\overline { CE } \Rightarrow \begin{cases} \angle BAD=\angle E \\ \angle DAC=\angle ACE \end{cases}\\ 又\overline { DA } 平分\angle BAC\Rightarrow \angle BAD=\angle DAC\Rightarrow \overline { AC } //\overline { AE } $$利用常見一的特性可知：$$\frac { \overline { BD }  }{ \overline { DC }  } =\frac { \overline { BA }  }{ \overline { AE }  } =\frac { \overline { BA }  }{ \overline { AC }  } \Rightarrow \frac { \overline { BA }  }{ \overline { AC }  } =\frac { \overline { BD }  }{ \overline { DC }  } $$

---

常見四
在常見一中，無論\(\overline{DE}\)是否平行\(\overline{BC}\)，皆有\(\triangle ADE:\triangle ABC=\overline{AD}\times\overline{AE}:\overline{AB}\times\overline{AC}\)。這個特性以前已說過，詳情可《按這裡》。
-- END --