解:$$\begin{cases} 2\left( x+y \right) +3\left( x-y \right) =5 \\ 5\left( x+y \right) +7\left( x-y \right) =12 \end{cases}\Rightarrow \begin{cases} 5x-y=5 \\ 12x-2y=12 \end{cases}\Rightarrow \begin{cases} 5x-y=5 \\ 6x-y=6 \end{cases}\\ \Rightarrow x=1,y=0\Rightarrow 2x+y=2$$,故選\(\bbox[red,2pt]{(A)}\)。
解:
令P的坐標為a,則Q=a+3、R=a+5、S=a+6。s-3p=16\(\Rightarrow a+6-3a=16\Rightarrow a=-5\)
因此q+2r=a+3+2a+10=3a+13=-15+13=-2,故選\(\bbox[red,2pt]{(A)}\)。
解:
令第2個數字為a,則此14個數字依序為
9、a、11-a、9、a、11-a、9、a、11-a、9、a、11-a、9、a
依題意倒數第3個為7,即11-a=7,因此a=4。x在第八個,即x=a=4,故選\(\bbox[red,2pt]{(B)}\)。解:$${ \left( 2+\sqrt { 5 } \right) }^{ 2017 }-4{ \left( 2+\sqrt { 5 } \right) }^{ 2016 }-{ \left( 2+\sqrt { 5 } \right) }^{ 2015 }\\ ={ \left( 2+\sqrt { 5 } \right) }^{ 2015 }\left[ { \left( 2+\sqrt { 5 } \right) }^{ 2 }-4\left( 2+\sqrt { 5 } \right) -1 \right] \\ ={ \left( 2+\sqrt { 5 } \right) }^{ 2015 }\left[ { \left( 9+4\sqrt { 5 } \right) }-4\left( 2+\sqrt { 5 } \right) -1 \right] { \\ =\left( 2+\sqrt { 5 } \right) }^{ 2015 }\times 0=0$$,故選\(\bbox[red,2pt]{(C)}\)。
解:
由題意可知:\(x^3+kx^2-4=P(x)(x^2+1)+(-x-6)\)。由於最高次方的係數為1,所以P(x)=x+a。
因此\(x^3+kx^2-4=(x+a)(x^2+1)+(-x-6)=x^3+ax^2+a-6\)
\(\Rightarrow a-6=-4\Rightarrow a=2=k\),故選\(\bbox[red,2pt]{(A)}\)。
解:
七個數依大小排序為1、1、3、4、5、6、8
(A)若另一個數為3,則數列變成1、1、3、3、4、5、6、8,中位數為3.5
(B)若另一個數為4,則數列變成1、1、3、4、4、5、6、8,中位數為4
(C)若另一個數為5,則數列變成1、1、3、4、5、5、6、8,中位數為4.5
,故選\(\bbox[red,2pt]{(D)}\)。
解:$$a^2-3ab-28b^2=0\Rightarrow (a-7b)(a+4b)=0\Rightarrow a=7b(\because a>0, b>0\therefore a\ne -4b)\\ \Rightarrow \frac{a-b}{a+b}=\frac{6b}{8b}=\frac{3}{4}$$,故選\(\bbox[red,2pt]{(D)}\)。
解:$$\begin{cases} \angle AED=26° \\ \angle AFB=32° \end{cases}\Rightarrow \begin{cases} \frac { \left( \widehat { AD } -\widehat { BC } \right) }{ 2 } =26° \\ \frac { \left( \widehat { AB } -\widehat { CD } \right) }{ 2 } =32° \end{cases}\Rightarrow \left( \widehat { AD } +\widehat { AB } )-(\widehat { CD } +\widehat { BC } \right) =116\\ 又\left( \widehat { AD } +\widehat { AB } )+(\widehat { CD } +\widehat { BC } \right) =360\Rightarrow \widehat { CD } +\widehat { BC } =122\Rightarrow \angle EAF=122/2=61$$,故選\(\bbox[red,2pt]{(D)}\)。
解:
f(x)=4x-2x(x+a)+b=\(-2x^2+(4-2a)x+b\)
由頂點坐標可知f(x)=\(-2{(x+2)}^2+3=-2x^2-8x-5\Rightarrow b=-5,a=6\Rightarrow 2a+3b=-3\),故選\(\bbox[red,2pt]{(A)}\)。
解:
令正三角形的邊長為a,如上圖。
\(\triangle BEF\)為等腰直角\(\Rightarrow \overline{BF}=\frac{a}{\sqrt{2}}\Rightarrow \overline{FC}=1-\frac{a}{\sqrt{2}}\)
在直角\(\triangle DCF中\)可知: \({\overline{DF}}^2={\overline{DC}}^2+{\overline{FC}}^2\)
\(\Rightarrow a^2=1+{1-\frac{a}{\sqrt{2}}}^2\Rightarrow a^2+2\sqrt{2}a-4=0\Rightarrow a=\sqrt{6}-\sqrt{2}\)
\(\triangle DEF面積=\frac{\sqrt{3}a^2}{4}=2\sqrt{3}-3\),故選\(\bbox[red,2pt]{(D)}\)。
解:
三角形任二邊之和大於第三邊,成為三角形的取法有:$$(\frac{1}{2},\frac{1}{3},\frac{1}{4}),(\frac{1}{2},\frac{1}{3},\frac{1}{5}),(\frac{1}{3},\frac{1}{4},\frac{1}{5}),(\frac{1}{3},\frac{1}{4},\frac{1}{6}),(\frac{1}{3},\frac{1}{5},\frac{1}{6}),(\frac{1}{4},\frac{1}{5},\frac{1}{6})$$共有六種情形,故選\(\bbox[red,2pt]{(C)}\)。
解:
令螢幕長為16k,寬為9k,則\((9k)^2+(16k)^2=(5\times 2.54)^2\Rightarrow k^2=\frac{(5\times 2.54)^2}{337}\)
\(\Rightarrow k=\frac{5\times 2.54}{\sqrt{337}}\approx\frac{12.7}{18.4}=0.69\Rightarrow 16k=11.04\),故選\(\bbox[red,2pt]{(B)}\)。
解:
再經y小時後,甲乙丙三線的生產量分別為:500+50y, 280+40y, 100+xy。由其比率可得
500+50y:280+40y=3:2\(\Rightarrow y=8\);又280+40y:100+xy=2:1,即600:100+8x=2:1\(\Rightarrow \)x=25,故選\(\bbox[red,2pt]{(C)}\)。
解:
令C點坐標為(a,\(a^2\)),由於C至\(\overline{AB}(Y軸)的距離為3\sqrt{3},所以C坐標為(3\sqrt{3},27)\)。A點與C點的垂直高度差距為3,所以A的坐標為(0, 27-3)=(0,24),故選\(\bbox[red,2pt]{(B)}\)。
解:
由題意可知: 2a+3b=44,其中a與b為原子筆的單價。
若不考慮丁品牌原子筆,2a+3b一定小於44,所以一定有丁品牌的原子筆,故選\(\bbox[red,2pt]{(D)}\)。
解:
延長\(\overline{BA}及\overline{ED}\)相交於F點,如上圖,則FDCA為一平行四邊形。
假設\(\triangle ACD面積=a\),則\(\triangle FAD面積也是a\)
由於\(\overline{FE}//\overline{AC}\Rightarrow \triangle ADF:\triangle CDE=\overline{FD}:\overline{DE}=a:27\)
同理,\(\overline{FA}:\overline{AB}=a:12\)$$\frac{\triangle FAD}{\triangle FBC}=\frac{\overline{FA}\times\overline{FD}}{\overline{FB}\times\overline{FE}}\Rightarrow \frac{a}{2a+39}=\frac{a^2}{(a+12)(a+27)}\\ \Rightarrow \frac{1}{2a+39}=\frac{a}{(a+12)(a+27)}\Rightarrow 2a^2+39a=a^2+39a+12\times 27\\ \Rightarrow a^2=12\times 27\Rightarrow a=18$$,故選\(\bbox[red,2pt]{(C)}\)。
解:
將長方體展開,可得上圖。螞蟻從P點走直線到Q點,其中\(\triangle PRQ\)為直角三角形。
因此,\({\overline{PQ}}^2={\overline{PR}}^2+{\overline{QR}}^2=3^2+14^2=205\Rightarrow \overline{PQ}=\sqrt{205}\),故選\(\bbox[red,2pt]{(A)}\)。
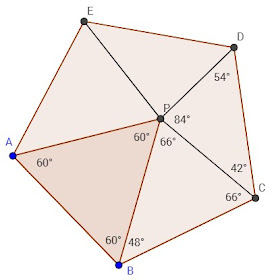
解:
正三角形每一內角為60度,正五邊形每一內角均為108度。
\(\angle PBC=108-60=48\),又\(\triangle BCP為等腰\Rightarrow \angle BPC=\angle BCP=(180-48)\div 2 = 66\)
\(\angle PCD=108-\angle BCP=108-66=42,\angle PDC=108\div 2=54\)
\(\Rightarrow \angle DPC=180-54-42=84\)
由三角形PCD之三內角可知\(\overline{PB}=\overline{CD}>\overline{PC}>\overline{PD}\),故選\(\bbox[red,2pt]{(A)}\)。
解:
第n層有6n-6個磁磚,第10層有60-6=54個磁磚。最外層磁磚有六個的外圍路徑是3,其餘皆是2,所以第10層的路徑總長是\(54\times 2+6\)=114,故選\(\bbox[red,2pt]{(B)}\)。
解:
令S1=第二次走到P1的距離,即S1=\(2\pi+1\)單位;
S2=第二次走到P2的距離,即S2=S1+\(4\pi+1\)單位;
...
\(S_n=S_{n-1}+2n\pi+1=(2\pi+4\pi+\cdots+2n\pi)+n = n(n+1)\pi+n\)
\(S_5=5\times 6\times\pi+5 \approx 66.8\Rightarrow \)第1次走到P6已走了67單位,再加逆時鐘走到Y軸再到X軸需要再走\(6\pi\approx18.84\),總距離已超過80,所以在第二象限,故選\(\bbox[red,2pt]{(B)}\)。
解:
上圖之等腰梯形符合條件(A)及條件(B),但不是平行四邊形
上圖之箏形符合條件(D),但不是平行四邊形
,故選\(\bbox[red,2pt]{(C)}\)。
解:$$\frac { 1911+x }{ x } =1+\frac { 1911 }{ x } =1+\frac { 3\times { 7 }^{ 2 }\times 13 }{ x } $$因此1911的因數有\(2\times 3\times 2\)=12個,但因數不能大於106,需扣除\(7^2\times 13\)、
\(3\times 7\times 13, 3\times 7^2及1911\)這四個大於106的因數,因此共有12-4=8個符合條件,故選\(\bbox[red,2pt]{(B)}\)。
解:
\(\overline{A_1B_1}\)的直線方程式為y=4x,而\(\overline{A_nB_n}\)的直線方程式為\(\overline{A_1B_1}\)右向平移n,因此\(\overline{A_nB_n}\)的直線方程式為y=4(x-n);同理\(\overline{A_2B_1}\)的直線方程式為y=-4x+4,\(\overline{A_nB_{n-1}}\)的直線方程式為y=-4(x-n)+4。
當n=10時,\(\left(\frac{52}{5},\frac{8}{5}\right)\)在直線y=4(x-10)上,故選\(\bbox[red,2pt]{(D)}\)。
解:
先任意畫連續兩個月曆(如上圖),紅字代表有營業,其餘黑字代表放假。其中同一星期皆放假的有兩個地方:一個是(3,10,17,24,31)、另一個是(6,13,20,27)。若觀察連續兩個月(6,13,20,27)接續(3,10,17,24,31)都放假,因此我們要將這兩個地方平移至星期日,可得下圖
所以1日在星期二會得到連續兩個月的週日都放假,故選\(\bbox[red,2pt]{(A)}\)。
解:
假設\(\triangle ABC\)為等要直角,且D為原點,C=(6,0),則各點坐標如下圖:
由以上坐標可求出\(\overline{BE}\)直線方程式為\(y=\frac{x}{2}+3,\overline{BF}\)的方程式為\(y=\frac{x}{5}+\frac{6}{5}\)
由兩方程式可求得Y截距,即\(\overline{GD}=3, \overline{HD}=\frac{6}{5} \Rightarrow \frac{\overline{AG}}{\overline{AH}}=\frac{\overline{AD}-\overline{GD}}{\overline{AD}-\overline{HD}}=\frac{6-3}{6-\frac{6}{5}}=\frac{5}{8}\)
,故選\(\bbox[red,2pt]{(C)}\)。
另解:
連結\(D, F\),並令\(\overline { GE } =a\),如上圖。$$\begin{cases} \overline { CF } :\overline { CE } =1:2 \\ \overline { CD } :\overline { CB } =1:2 \end{cases}\Rightarrow \triangle CDF\sim \triangle CBE\Rightarrow \overline { CF } //\overline { BE } \Rightarrow \triangle AGE\sim \triangle ADF\\ 又\begin{cases} \angle DHF=\angle GHB \\ \overline { DF } //\overline { BG } \end{cases}\Rightarrow \triangle HDF\sim \triangle HGB\\ \triangle AGE\sim \triangle ADF\Rightarrow \overline { DF } =2\overline { GE } =2a\Rightarrow \overline { BE } =4a\left( \because \triangle CDF\sim \triangle CBE \right) \Rightarrow \overline { BG } =3a\\ \Rightarrow \begin{cases} \triangle HDF\sim \triangle HGB\Rightarrow \frac { \overline { GH } }{ \overline { HD } } =\frac { \overline { BG } }{ \overline { DF } } =\frac { 3a }{ 2a } =\frac { 3 }{ 2 } \Rightarrow \overline { GH } =\frac { 3 }{ 5 } \overline { GD } \\ \triangle AGE\sim \triangle ADF\Rightarrow \overline { AG } =\overline { GD } \end{cases}\\ \Rightarrow \frac { \overline { AG } }{ \overline { AH } } =\frac { \overline { AG } }{ \overline { AG } +\overline { GH } } =\frac { \overline { AG } }{ \overline { AG } +\frac { 3 }{ 5 } \overline { GD } } =\frac { \overline { AG } }{ \overline { AG } +\frac { 3 }{ 5 } \overline { AG } } =\bbox[red,2pt]{\frac { 5 }{ 8 }} $$
-- end --



































第25題用孟氏定理會比較正確
回覆刪除假如AG=a, GH=b, HD=c
則△ACD和△FCB中得c/(a+b)=1/4
在△ACD和△ECB中得(b+c)/a=1/1
由兩式加減消去c可得a:b=5:3
所求=a/(a+b)=5/(5+3)=5/8
國中大多數應該不會用孟式吧
刪除可是國中也不會用座標假設吧! 有沒有國中生真正能用的方法呢?
刪除連接DF,CF:ef=1:1,CD:DB=1:1
刪除做cdf~cbe,同時age~adf
然後對應的AG:AH即可找出
增加「另解」,這樣就不用座標假設,謝謝大家的意見!
刪除第16題應為三角形FAD/三角形FBE
回覆刪除hi
回覆刪除