104年高考三級-工程數學詳解

104年公務人員高等考試三級考試

類科組：電子工程、電子工程、醫學工程
科        目：工程數學

甲、申論題部份：(50分)

解：$$y=a_{ 0 }+a_{ 1 }x+a_{ 2 }x^{ 2 }+\cdots +a_{ n }x^{ n }+\cdots \Rightarrow y'=a_{ 1 }+2a_{ 2 }x+3a_{ 3 }x^{ 2 }+\cdots +na_{ n }x^{ n-1 }+\cdots \\ 代入原式可得a_{ 1 }+2a_{ 2 }x+3a_{ 3 }x^{ 2 }+\cdots +na_{ n }x^{ n-1 }+\cdots =2a_{ 0 }x+2a_{ 1 }x^{ 2 }+\cdots +2a_{ n }x^{ n+1 }+\cdots \\ \Rightarrow \begin{cases} a_{ 1 }=0 \\ 2a_{ 2 }=2a_{ 0 } \\ 3a_{ 3 }=2a_{ 1 } \\ 4a_{ 4 }=2a_{ 2 } \\ 5a_{ 5 }=2a_{ 3 } \\ 6a_{ 6 }=2a_{ 4 } \\ na_{ n }=2a_{ n-2 } \end{cases}\Rightarrow a_{ n }=\begin{cases} 0 & n=2k-1,k=1,2,\dots  \\ \frac { a_{ 2k-2 } }{ k } =\frac { { a }_{ 0 } }{ k! }  & n=2k,k=1,2,\dots  \end{cases}\\ \Rightarrow \bbox[red,2pt]{y=a_{ 0 }+a_{ 0 }x^{ 2 }+\frac { 1 }{ 2 } a_{ 0 }x^{ 4 }+\frac { 1 }{ 6 } a_{ 0 }x^{ 6 }+\cdots +\frac { 1 }{ k! } a_{ 0 }x^{ 2k }+\cdots} ,k=1,2,\dots  ,a_0為一常數$$

---

解：$$\begin{cases} det\left( M \right) =36 \\ tr\left( M \right) =10 \end{cases}\Rightarrow \begin{cases} \lambda _{ 1 }\lambda _{ 2 }\lambda _{ 3 }=\lambda _{ 1 }\lambda _{ 2 }^{ 2 }=36 \\ \lambda _{ 1 }+\lambda _{ 2 }+\lambda _{ 3 }=\lambda _{ 1 }+2\lambda _{ 2 }=10 \end{cases}\Rightarrow \begin{cases} \lambda _{ 1 }=4 \\ \lambda _{ 2 }=\lambda _{ 3 }=3 \end{cases}\\ det(M-\lambda I)=0\Rightarrow det(M-I-\left( \lambda -I \right) I)=0\Rightarrow M-I的特徵值為\lambda _{ 1 }-1,\lambda _{ 2 }-1,\lambda _{ 3 }-1\\ \Rightarrow M-I=P\left[ \begin{matrix} \lambda _{ 1 }-1 & 0 & 0 \\ 0 & \lambda _{ 2 }-1 & 0 \\ 0 & 0 & \lambda _{ 3 }-1 \end{matrix} \right] { P }^{ -1 }\Rightarrow { \left( M-I \right)  }^{ 2 }\\=P\left[ \begin{matrix} { \left( \lambda _{ 1 }-1 \right)  }^{ 2 } & 0 & 0 \\ 0 & { \left( \lambda _{ 2 }-1 \right)  }^{ 2 } & 0 \\ 0 & 0 & { \left( \lambda _{ 3 }-1 \right)  }^{ 2 } \end{matrix} \right] { P }^{ -1 }\\ \Rightarrow { \left( M-I \right)  }^{ 2 }的特徵值為{ \left( \lambda _{ 1 }-1 \right)  }^{ 2 },{ \left( \lambda _{ 2 }-1 \right)  }^{ 2 },{ \left( \lambda _{ 3 }-1 \right)  }^{ 2 },即\bbox[red,2pt]{9,4,4}$$

---

解：
題目有誤! \(2\le x\le 5\)應該是\(2\le \bbox[red,2pt]{y}\le 5\)
(一)

由\(x,y\)的範圍可知定義域\(D\)為一面積為\(2\times 3=6\)的矩形，如上圖，又因直線\(x+y=w\)將矩形切分成三個區域，即\(R_1:\{3\le w< 5\},R_2:\{5\le w<6\}, R_3:\{6\le w< 8\}\)
我們先求累積分布函數\(F_W(w)=f_W(x+y<w)\)

\(3\le w<5 \Rightarrow \triangle AEF面積=(w-3)^2\div 2=(w^2-6w+9)\div 2\)

\(5\le w<6\Rightarrow 梯形 EBAF面積=\frac{((w-5)+(w-5+2))2}{2}=2w-8\)

\(6\le w<8\Rightarrow  ABEHD面積=6-\triangle CEH=6-(w-8)^2\div 2=-w^2/2+8w-26\)

由以上討論可知$$area\left( D \right) \times F_{ W }\left( w \right) =6F_{ W }\left( w \right) =\begin{cases} \frac { 1 }{ 2 } w^{ 2 }-3w+\frac { 9 }{ 2 }  & 3\le w<5 \\ 2w-8 & 5\le w<6 \\ -\frac { 1 }{ 2 } w^{ 2 }+8w+26 & 6\le w<8 \end{cases}\\ \Rightarrow F_{ W }\left( w \right) =\begin{cases} \frac { 1 }{ 12 } w^{ 2 }-\frac { 1 }{ 2 } w+\frac { 9 }{ 12 }  & 3\le w<5 \\ \frac { 1 }{ 3 } w-\frac { 4 }{ 3 }  & 5\le w<6 \\ -\frac { 1 }{ 12 } w^{ 2 }+\frac { 4 }{ 3 } w+\frac { 13 }{ 3 }  & 6\le w<8 \end{cases}\\ \Rightarrow f_{ W }\left( w \right) =F'_{ W }\left( w \right) =\bbox[red,2pt]{\begin{cases} \frac { 1 }{ 6 } w-\frac { 1 }{ 2 }  & 3\le w<5 \\ \frac { 1 }{ 3 }  & 5\le w<6 \\ \frac { 4 }{ 3 } -\frac { 1 }{ 6 } w & 6\le w<8 \end{cases}}$$(二)圖形如下:

---

解：

由\(D\)之定義可知其為四分之一圓，原點為圓心，半徑為2，如上圖。$$\begin{cases} x=r\cos { \theta  }  \\ y=r\sin { \theta  }  \end{cases}\Rightarrow \iint _{ D }{ { \left( x^{ 2 }+y^{ 2 } \right)  }^{ 4/3 }dA } =\int _{ 0 }^{ \pi /2 }{ \int _{ 0 }^{ 2 }{ \left( r^{ 2 } \right) ^{ 4/3 } } rdrd\theta  } =\int _{ 0 }^{ \pi /2 }{ \int _{ 0 }^{ 2 }{ r^{ 11/3 } } drd\theta  } \\ =\int _{ 0 }^{ \pi /2 }{ \left. \left[ \frac { 3 }{ 14 } r^{ 14/3 } \right]  \right| _{ 0 }^{ 2 }d\theta  } =\frac { 3 }{ 14 } \int _{ 0 }^{ \pi /2 }{ { 2 }^{ 14/3 }d\theta  } =\frac { 3 }{ 14 } \cdot { 2 }^{ 14/3 }\cdot \frac { \pi  }{ 2 } =\frac { 3\pi  }{ 14 } \cdot 8\cdot { 2 }^{ 2/3 }\\ =\bbox[red,2pt]{\frac { 12\sqrt [ 3 ]{ 4 }  }{ 7 } \pi }$$

---

乙、測驗題部分：(50分)

解：$$\nabla \times F=\left| \begin{matrix} \vec { i }  & \vec { j }  & \vec { k }  \\ \frac { \partial  }{ \partial x }  & \frac { \partial  }{ \partial y }  & \frac { \partial  }{ \partial z }  \\ 2xy & x{ e }^{ y } & 2z \end{matrix} \right| \\ =\frac { \partial  }{ \partial y } 2z\vec { i } +\frac { \partial  }{ \partial x } x{ e }^{ y }\vec { k } +\frac { \partial  }{ \partial z } 2xy\vec { j } -\frac { \partial  }{ \partial y } 2xy\vec { k } -\frac { \partial  }{ \partial x } 2z-\frac { \partial  }{ \partial z } x{ e }^{ y }\vec { i } \\ ={ e }^{ y }\vec { k } -2x\vec { k } =\left( { e }^{ y }-2x \right) \vec { k } \Rightarrow \left. \nabla \times F \right| _{ \left( -1,0,1 \right)  }=\left( { e }^{ 0 }+2 \right) \vec { k } =3\vec { k } ，故選\bbox[red,2pt]{(D)}$$

---

解：$$F=x^{ 3 }\vec { i } +x^{ 2 }y\vec { j } +x^{ 2 }z\vec { k } \Rightarrow \unicode{x222F} _{ S }{ F\cdot dA } =\iiint _{ T }{ \nabla \cdot F } dV=\iiint _{ T }{ \left( \frac { \partial  }{ \partial x } x^{ 3 }+\frac { \partial  }{ \partial y } x^{ 2 }y+\frac { \partial  }{ \partial z } x^{ 2 }z \right)  } dV\\ =\iiint _{ T }{ \left( 5x^{ 2 } \right)  } dV\\ 圓柱面:\left\{ (x=r\cos { \theta  } ,y=r\sin { \theta  } ,z):0\le r\le a,0\le z\le b,0\le \theta \le 2\pi  \right\} ,因此上式可寫成\\ \iiint _{ T }{ \left( 5x^{ 2 } \right)  } dV=\int _{ 0 }^{ b }{ \int _{ 0 }^{ 2\pi  }{ \int _{ 0 }^{ a }{ 5r^{ 2 }\cos ^{ 2 }{ \theta  }  } rdrd\theta dz }  } =\int _{ 0 }^{ b }{ \int _{ 0 }^{ 2\pi  }{ \int _{ 0 }^{ a }{ 5r^{ 3 }\cos ^{ 2 }{ \theta  }  } drd\theta dz }  } \\ =\int _{ 0 }^{ b }{ \int _{ 0 }^{ 2\pi  }{ \cos ^{ 2 }{ \theta  } \left. \left[ \frac { 5 }{ 4 } r^{ 4 } \right]  \right| _{ 0 }^{ a }d\theta dz }  } =\frac { 5 }{ 4 } a^{ 4 }\int _{ 0 }^{ b }{ \int _{ 0 }^{ 2\pi  }{ \cos ^{ 2 }{ \theta  } d\theta dz }  } =\frac { 5 }{ 4 } a^{ 4 }\int _{ 0 }^{ b }{ \int _{ 0 }^{ 2\pi  }{ \frac { 1+\cos { 2\theta  }  }{ 2 } d\theta dz }  } \\ =\frac { 5 }{ 4 } a^{ 4 }\int _{ 0 }^{ b }{ \left. \left[ \frac { 1 }{ 2 } \theta +\frac { 1 }{ 4 } \sin { 2\theta  }  \right]  \right| _{ 0 }^{ 2\pi  } } dz=\frac { 5\pi  }{ 4 } a^{ 4 }\int _{ 0 }^{ b }{ 1 } dz=\frac { 5\pi  }{ 4 } a^{ 4 }b，故選\bbox[red,2pt]{(D)}$$

---

解：$$\nabla \cdot \varphi =\frac { \partial  }{ \partial x } xy+\frac { \partial  }{ \partial y } \left( -yz \right) +\frac { \partial  }{ \partial z } xyz=y-z+xy\\ \Rightarrow \left. \nabla \cdot \varphi   \right| _{ \left( 0,-1,1 \right)  }=-1-1+0=-2，故選\bbox[red,2pt]{(B)}$$

---

解：$$F+G=\vec { i } -3\vec { k } +2\vec { j } \Rightarrow \left\| F+G \right\| _{ 2 }=\sqrt { 1^{ 2 }+2^{ 2 }+(-3)^{ 2 } } =\sqrt { 14 }，故選\bbox[red,2pt]{(D)} $$

---

解：$$det\left( M-\lambda I \right) =0\Rightarrow \left[ \begin{matrix} 1-\lambda  & -1 & -1 \\ 1 & 3-\lambda  & 1 \\ -3 & 1 & -1-\lambda  \end{matrix} \right] =\left( \lambda -2 \right) \left( \lambda +2 \right) \left( \lambda -3 \right) =0\\ \Rightarrow \lambda =\pm 2,3，故選\bbox[red,2pt]{(B)}$$

---

解：$$\left| \begin{matrix} a+g & b+h & c+i \\ -2d & -2e & -2f \\ -2g & -2h & -2i \end{matrix} \right| =4\left| \begin{matrix} a+g & b+h & c+i \\ d & e & f \\ g & h & i \end{matrix} \right| =4\left| \begin{matrix} a & b & c \\ d & e & f \\ g & h & i \end{matrix} \right| =4\times 20=80，故選\bbox[red,2pt]{(D)} $$

---

解：$$det\left( A-\lambda I \right) =0\Rightarrow \left| \begin{matrix} -\lambda  & 1 & 0 \\ 0 & -\lambda  & 1 \\ 4 & -17 & 8-\lambda  \end{matrix} \right| =\lambda ^{ 2 }\left( 8-\lambda  \right) +4-17\lambda =\left( \lambda -4 \right) \left( \lambda ^{ 2 }-4\lambda +1 \right) =0\\ \Rightarrow \lambda =4,2\pm \sqrt { 3 } ，故選\bbox[red,2pt]{(A)}$$

---

解：$$det\left( M-\lambda I \right) =0\Rightarrow \left| \begin{matrix} 2-\lambda  & 1 & 1 \\ -1 & 2-\lambda  & -1 \\ -1 & 1 & 3-\lambda  \end{matrix} \right| =\lambda ^{ 3 }-7\lambda ^{ 2 }+19\lambda -19=0\\ \Rightarrow M^{ 3 }-7M^{ 2 }+19M-19I=0\Rightarrow M^{ 3 }-7M^{ 2 }+19M=\left[ \begin{matrix} 19 & 0 & 0 \\ 0 & 19 & 0 \\ 0 & 0 & 19 \end{matrix} \right] \\ \Rightarrow M^{ 3 }=7M^{ 2 }-19M+19I=7\left[ \begin{matrix} 2 & 1 & 1 \\ -1 & 2 & -1 \\ -1 & 1 & 3 \end{matrix} \right] ^{ 2 }-19\left[ \begin{matrix} 2 & 1 & 1 \\ -1 & 2 & -1 \\ -1 & 1 & 3 \end{matrix} \right] +\left[ \begin{matrix} 19 & 0 & 0 \\ 0 & 19 & 0 \\ 0 & 0 & 19 \end{matrix} \right] \\ =\left[ \begin{matrix} 14 & 35 & 28 \\ -21 & 14 & -42 \\ -42 & 28 & 49 \end{matrix} \right] -\left[ \begin{matrix} 38 & 19 & 19 \\ -19 & 38 & -19 \\ -19 & 19 & 57 \end{matrix} \right] +\left[ \begin{matrix} 19 & 0 & 0 \\ 0 & 19 & 0 \\ 0 & 0 & 19 \end{matrix} \right] =\left[ \begin{matrix} -5 & 16 & 9 \\ -2 & -5 & -23 \\ -23 & 9 & 11 \end{matrix} \right] \\ 由以上可知選項(A)(B)(C)皆正確\\ \lambda ^{ 3 }=7\lambda ^{ 2 }-19\lambda +19\Rightarrow \lambda ^{ 4 }=7\lambda ^{ 3 }-19\lambda ^{ 2 }+19\lambda =7\left( 7\lambda ^{ 2 }-19\lambda +19 \right) -19\lambda ^{ 2 }+19\lambda =30\lambda ^{ 2 }-114\lambda +133\\ \Rightarrow M^{ 4 }=30M^{ 2 }-114M+133I\left( \neq 139 \right) \Rightarrow 選項(D)錯誤!，故選\bbox[red,2pt]{(D)}$$

---

解：$$\begin{cases} f\left( z \right) =z^{ 6 }+z^{ 3 }-2z \\ g\left( z \right) =-5z^{ 4 } \end{cases}\Rightarrow p\left( z \right) =z^{ 6 }-5z^{ 4 }+z^{ 3 }-2z=f\left( z \right) +g\left( z \right) \\ 在|z|=1\Rightarrow \left| f\left( z \right)  \right| =\left| z^{ 6 }+z^{ 3 }-2z \right| \le 1+1+2=4<5=\left| -5z^{ 4 } \right| =\left| g\left( z \right)  \right| \\ \Rightarrow f\left( z \right) +g\left( z \right) 與g\left( z \right) 有相同個數的零點,即g\left( z \right) =-5z^{ 4 }=0有4重根，故選\bbox[red,2pt]{(D)}$$

---

解：$$f\left( z \right) =\frac { 5z-2 }{ z\left( z-1 \right)  } \Rightarrow z=0,z=1為單極點\\ \Rightarrow \int _{ C }{ f\left( z \right)  } =2\pi i\left( \frac { -2 }{ -1 } +\frac { 5-2 }{ 1 }  \right) =2\pi i\times 5=10\pi i，故選\bbox[red,2pt]{(D)}$$

---

解：$$\left( 6-2i \right) \left( 1+i \right) =6+6i-2i+2=8+4i\Rightarrow \overline { \left( 6-2i \right) \left( 1+i \right)  } =\overline { 8+4i } =8-4i，故選\bbox[red,2pt]{(C)}$$

---

解：$$f\left( t \right) =\begin{cases} 0 & ,0\le t<1 \\ 1 & ,1\le t<3 \\ -1 & ,3\le t \end{cases}=u\left( t-1 \right) -2u\left( t-3 \right) \Rightarrow L\left\{ f\left( t \right)  \right\} =L\left\{ u\left( t-1 \right) -2u\left( t-3 \right)  \right\} \\ =\frac { 1 }{ s } { e }^{ -s }-\frac { 2 }{ s } { e }^{ -3s }，故選\bbox[red,2pt]{(A)}$$

---

解：$$au_{ xx }+bu_{ xy }+cu_{ yy }=0\Rightarrow 若b^{ 2 }<4ac則為橢圓\\ 僅(D)u_{xx}+u_{yy}=0\Rightarrow b^2-4ac=0-4<0符合條件，故選\bbox[red,2pt]{(D)}$$

---

解：$$xy'+2y=x^{ 3 }y^{ 2 }\Rightarrow \frac { 1 }{ x^{ 2 } } y'+\frac { 2 }{ x^{ 3 } } y=y^{ 2 }\\ 令u=\frac { 1 }{ y } \Rightarrow u'=-\frac { y' }{ { y }^{ 2 } } =-{ u }^{ 2 }y'\Rightarrow y'=-\frac { u' }{ { u }^{ 2 } } 代入上式可得:\\ -\frac { u' }{ x^{ 2 }{ u }^{ 2 } } +\frac { 2 }{ x^{ 3 }u } =\frac { 1 }{ u^{ 2 } } \Rightarrow -xu'+2u=x^{ 3 }\Rightarrow u=u_{ h }+u_{ p }=Cx^{ 2 }-x^{ 3 }=\frac { 1 }{ y } \\ \Rightarrow y=\frac { 1 }{ Cx^{ 2 }-x^{ 3 } } ，故選\bbox[red,2pt]{(B)}$$

---

解：$$F\left( s \right) =L\left\{ \frac { t^{ 2 } }{ 2 } -\frac { t }{ \pi  } +\frac { e^{ \pi t }-1 }{ \pi ^{ 2 } }  \right\} =\frac { 1 }{ 2 } L\left\{ t^{ 2 } \right\} -\frac { 1 }{ \pi  } L\left\{ t \right\} +\frac { 1 }{ \pi ^{ 2 } } L\left\{ e^{ \pi t } \right\} -\frac { 1 }{ \pi ^{ 2 } } L\left\{ 1 \right\} \\ =\frac { 1 }{ 2 } \cdot \frac { 2 }{ s^{ 3 } } -\frac { 1 }{ \pi  } \cdot \frac { 1 }{ s^{ 2 } } +\frac { 1 }{ \pi ^{ 2 } } \cdot \frac { 1 }{ s-\pi  } -\frac { 1 }{ \pi ^{ 2 } } \cdot \frac { 1 }{ s } =\frac { 1 }{ s^{ 3 } } -\frac { 1 }{ s^{ 2 }\pi  } +\frac { 1 }{ \pi ^{ 2 }\left( s-\pi  \right)  } -\frac { 1 }{ s\pi ^{ 2 } } \\ \Rightarrow F\left( 2\pi  \right) =\frac { 1 }{ 8\pi ^{ 3 } } -\frac { 1 }{ 4\pi ^{ 3 } } +\frac { 1 }{ \pi ^{ 3 } } -\frac { 1 }{ 2\pi ^{ 3 } } =\frac { 1 }{ 8\pi ^{ 3 } } \left( 1-2+8-4 \right) =\frac { 3 }{ 8\pi ^{ 3 } } ，故選\bbox[red,2pt]{(A)}$$

---

解：$$f\left( t \right) =\begin{cases} -\frac { \pi  }{ 2 } , & -\pi <t<0 \\ \frac { \pi  }{ 2 } , & 0<t<\pi  \end{cases}=2\left( \sin { t } +\frac { \sin { 3t }  }{ 3 } +\frac { \sin { 5t }  }{ 5 } +\cdots  \right) \\ \Rightarrow f\left( \frac { \pi  }{ 2 }  \right) =\frac { \pi  }{ 2 } =2\left( \sin { \frac { \pi  }{ 2 }  } +\frac { \sin { 3\pi /2 }  }{ 3 } +\frac { \sin { 5\pi /2 }  }{ 5 } +\cdots  \right) \\ \Rightarrow \pi =4\left( \sin { \frac { \pi  }{ 2 }  } +\frac { \sin { 3\pi /2 }  }{ 3 } +\frac { \sin { 5\pi /2 }  }{ 5 } +\cdots  \right) =4\left( 1-\frac { 1 }{ 3 } +\frac { 1 }{ 5 } -\cdots  \right) \\ =4\cdot \sum _{ n=1 }^{ \infty  }{ \left( \frac { 1 }{ 2n-1 }  \right) { \left( -1 \right)  }^{ n+1 } } =\sum _{ n=1 }^{ \infty  }{ \left( \frac { 2 }{ n-\frac { 1 }{ 2 }  }  \right) { \left( -1 \right)  }^{ n+1 } } ，故選\bbox[red,2pt]{(D)}$$

---

解：$$\nabla ^{ 2 }u\equiv u_{ xx }+u_{ yy }+u_{ zz }\\ \left( A \right) \nabla ^{ 2 }\left( x+y+xy+4z \right) =0+0+0=0\\ \left( B \right) \nabla ^{ 2 }\left( x^{ 2 }+y^{ 2 }+xy+yz+zx \right) =2+2+0=4\neq 0\\ \left( C \right) \nabla ^{ 2 }\left( x^{ 3 }-3xy^{ 2 }zx \right) =6-6+0=0\\ \left( D \right) \nabla ^{ 2 }\left( \ln { \left( x^{ 2 }+y^{ 2 } \right)  }  \right) =\frac { 2y^{ 2 }-2x^{ 2 } }{ { \left( x^{ 2 }+y^{ 2 } \right)  }^{ 2 } } +\frac { 2x^{ 2 }-2y^{ 2 } }{ { \left( x^{ 2 }+y^{ 2 } \right)  }^{ 2 } } +0=0\\ ，故選\bbox[red,2pt]{(B)}$$

---

解：$$P\left( X\le 5\mid X\ge 2 \right) =\frac { P\left( 2\le X\le 5 \right) }{ P\left( x\ge 2 \right) } =\frac { \left( 1-F\left( 2 \right) \right) -\left( 1-F\left( 5 \right) \right) }{ 1-F\left( 2 \right) } =\frac { \frac { 3 }{ 4 } -\frac { 1 }{ 4 } }{ \frac { 3 }{ 4 } } =\frac { 2 }{ 3 } ，故選\bbox[red,2pt]{(B)}$$

---

解：
假設二枚錢幣分別為A及B，錢幣A出現正面的機率為1/2，錢幣B出現正面的機率為1/10；
情況一：選出錢幣A的機率為1/2，投擲第1次出現正面的機率為1/2，因此機率為\(\frac{1}{2}\times\frac{1}{2}=\frac{1}{4}\);
情況二：選出錢幣B的機率為1/2，投擲第1次出現正面的機率為1/10，因此機率為\(\frac{1}{2}\times\frac{1}{10}=\frac{1}{20}\);
以上兩種情況的機率為\(\frac{1}{4}+\frac{1}{20}=\frac{6}{20}=\frac{3}{10}\)，故選\(\bbox[red,2pt]{(D)}\)

---

解：

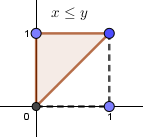
積分區域如上圖，因此\(P(X<Y)=\int_0^1\int_0^y{4xy\,dx\,dy}=\int_0^1{2y^3\,dy}=\frac{1}{2}\)，故選\(\bbox[red,2pt]{(B)}\)

---

考選部未公布申論題答案，解題僅供參考