臺北市立建國高級中學109學年度第一次代理教師甄選
數學科題目卷
解:$$\cases{\log_3 x-y=1\\ x-3^y=2\sqrt 3} \Rightarrow \cases{3^{y+1}=x \\ 3^y=x-2\sqrt 3} \Rightarrow x=3(x-2\sqrt 3) \Rightarrow x=3\sqrt 3 \Rightarrow 3^y=3\sqrt 3-2\sqrt 3=3^{1/2} \\ \Rightarrow y=1/2 \Rightarrow (x,y)=\bbox[red,2pt]{(3\sqrt 3,1/2)}$$

解:$$\begin{bmatrix} a& b& 1& 2\\ c & d& 4& 3\end{bmatrix} \xrightarrow{列運算}\begin{bmatrix} 1& 0& 3& 4\\ 0 & 1& 5& 7 \end{bmatrix}\\ \Rightarrow \cases{(a,b,1,2)=m(1,0,3,4) +n(0,1,5,7) =(m,n,3m+5n,4m+7n) \\ (c,d,4,3) = p(1,0,3,4)+q(0,1,5,7) =(p,q,3p+5q,4p+7q)} \\ \Rightarrow \cases{\cases{3m+5n=1\\ 4m+7n=2}\\ \cases{3p+5q=4\\ 4p+7q=3}} \Rightarrow \cases{(m,n)=(-3,2) \\ (p,q)=(13,-7)} \Rightarrow \cases{a=m=-3\\ b=n=2\\ c=p=13\\ d=q=-7} \\ \Rightarrow \begin{bmatrix} a& b\\ c & d\end{bmatrix} =\bbox[red,2pt]{\begin{bmatrix} -3& 2\\ 13 & -7\end{bmatrix}}$$

解:$${1\over \sqrt{a_1}+\sqrt{a_2}} +{1\over \sqrt{a_2}+\sqrt{a_3}} +{1\over \sqrt{a_3}+\sqrt{a_4}} +\cdots +{1\over \sqrt{a_{80}}+\sqrt{a_{81}}} \\ ={\sqrt{a_1}-\sqrt{a_2}\over a_1-a_2} +{\sqrt{a_2}-\sqrt{a_3}\over a_2-a_3} +{\sqrt{a_3}-\sqrt{a_4}\over a_3-a_4} +\cdots +{ \sqrt{a_{80}} -\sqrt{a_{81}}\over a_{80}-a_{81}} \\ =-{1\over 7}(\sqrt{a_1}-\sqrt{a_2} +\sqrt{a_2}-\sqrt{a_3}+\sqrt{a_3}-\sqrt{a_4}+\cdots +\sqrt{a_{80}} -\sqrt{a_{81}})\\ =-{1\over 7}(\sqrt{a_1} -\sqrt{a_{81}}) = -{1\over 7}(\sqrt{16} -\sqrt{16+80\times 7}) =-{1\over 7}(4-24)\\ =\bbox[red, 2pt]{20\over 7}$$
解:$${1\over \sqrt{a_1}+\sqrt{a_2}} +{1\over \sqrt{a_2}+\sqrt{a_3}} +{1\over \sqrt{a_3}+\sqrt{a_4}} +\cdots +{1\over \sqrt{a_{80}}+\sqrt{a_{81}}} \\ ={\sqrt{a_1}-\sqrt{a_2}\over a_1-a_2} +{\sqrt{a_2}-\sqrt{a_3}\over a_2-a_3} +{\sqrt{a_3}-\sqrt{a_4}\over a_3-a_4} +\cdots +{ \sqrt{a_{80}} -\sqrt{a_{81}}\over a_{80}-a_{81}} \\ =-{1\over 7}(\sqrt{a_1}-\sqrt{a_2} +\sqrt{a_2}-\sqrt{a_3}+\sqrt{a_3}-\sqrt{a_4}+\cdots +\sqrt{a_{80}} -\sqrt{a_{81}})\\ =-{1\over 7}(\sqrt{a_1} -\sqrt{a_{81}}) = -{1\over 7}(\sqrt{16} -\sqrt{16+80\times 7}) =-{1\over 7}(4-24)\\ =\bbox[red, 2pt]{20\over 7}$$
4. 已知建仔每天中午到熱食部只從紅燒牛肉麵、肉麻雙醬麵、 貢丸麵、雞排飯、 柳葉魚飯 5 種餐中選一種來點, 若前一天中午點飯, 則當天中午就從前一天中午沒點過的 4 種餐中隨機點一種; 若前一天中午點麵, 則當天中午就從雞排飯、 柳葉魚飯這 2 種飯中隨機點一種。 假設熱食部每天中午開門,供餐充足,沒有不能點的情形。 若建仔於 7 月6 日中午點了貢丸麵,則 4 天後(7 月 10 日)中午也是點貢丸麵的機率為_____ 。
解:$$令\cases{A群(麵)\cases{A1:牛肉麵\\ A2:肉麻雙醬麵\\ A3:貢丸麵}\\ B群(飯)\cases{B1:雞排飯\\ B2:柳葉魚飯}}\\ A3\to B1\to B2\to B1\to A3\Rightarrow 機率為{1\over 2}\times {1\over 4}\times {1\over 4}\times {1\over 4} ={1\over 128}\\ A3\to B1\to A群\to B1\to A3\Rightarrow 機率為{1\over 2}\times {3\over 4}\times {1\over 2}\times {1\over 4} ={3\over 64}\\ A3\to B1\to A群\to B2\to A3\Rightarrow 機率為{1\over 2}\times {3\over 4}\times {1\over 2}\times {1\over 4} ={3\over 64}\\ 因此A3\to B1\to \cdots\to A3機率為{1\over 128}+{3\over 64}+ {3\over 64}={13\over 128};\\同理A3\to B2\to \cdots\to A3機率也是{13\over 128};\\因此4天後也是點貢丸麵(A3)的機率為{13\over 128}+{13\over 128} =\bbox[red,2pt]{13\over 64}$$

解:$$\cases{A(-9,0)\\ B(0,-4)} \Rightarrow \cases{\overleftrightarrow{AB}: 4x+9y+36=0 \\\overline{AB}= \sqrt{9^2+4^2}= \sqrt{97}}\\ {4a+{9\over a} \ge 2\sqrt{4a\cdot {9\over a}}}=12 \Rightarrow P(a,{1\over a}) \Rightarrow d(P,\overleftrightarrow{AB})= {4a+{9\over a}+36 \over \sqrt{97}} \ge {48\over \sqrt{97}} \\ \Rightarrow \triangle ABP 面積={1\over 2}\times \overline{AB}\times d(P,\overleftrightarrow{AB}) \ge {1\over 2}\times \sqrt{97}\times{48\over \sqrt{97}} =\bbox[red,2pt]{24}$$

解:$$\cases{x^3-1 = (x-1)(x^2+x+1)\\ x^3+2x^2+2x+1= (x+1) (x^2+x+1)} \\\Rightarrow f(x)=\cases{P(x)(x-1)(x^2+x+1) +ax^2-bx+1 \\ Q(x)(x+1) (x^2+x+1)-3ax^2+bx+5}\\ 令x^2+x+1=0 \Rightarrow f(x)=\cases{ax^2-bx+1 \\-3ax^2+bx+5} =\cases{a(-x-1)-bx+1 \\-3a(-x-1)+bx+5} (\because x^2=-x-1)\\=\cases{(-a-b)x-a+1 \\(3a+b)x+3a+5} \Rightarrow \cases{-a-b=3a+b\\ -a+1=3a+5} \Rightarrow (a,b)=\bbox[red,2pt]{(-1,2)}$$

解:$$S_n,a_{n+1},S_{n+1} 成等差\Rightarrow a_{n+1}-S_n =S_{n+1}-a_{n+1} \Rightarrow S_{n+1}=2a_{n+1}-S_n \Rightarrow S_{n+1} -S_n=2a_{n+1}-2S_n \\\Rightarrow a_{n+1}=2a_{n+1}-2S_n \Rightarrow a_{n+1}=2S_n\\ \Rightarrow a_2=2S_1=2a_1 \Rightarrow S_2= a_1+a_2=3a_1 \Rightarrow a_3=2S_2 = 6a_1 \Rightarrow S_3= a_3+S_2=9a_1 \\ \Rightarrow a_4=2S_3 =18a_1 \Rightarrow S_4 = a_4+S_3 =27a_1 \Rightarrow a_5=2S_4 =54a_1 =324 \Rightarrow a_1= \bbox[red,2pt]{6}$$

解:$$\begin{array}{} a& b& c& d &排列數\\\hline 1 & 0 & 1 & 2 & 6\\& 0 & 1 & 3 & 6 \\ & 0 & 2 & 2& 3\\ & 0 & 2 & 3& 6\\ &0 &3 &3 & 3\\\hdashline & 1& 2& 2 & 3 \\ & 1 & 2& 3& 6\\ & 1 & 3& 3& 3\\\hdashline & 2 & 2& 2& 1\\ & 2& 2& 3& 3\\ & 2 & 3& 3& 3\\ & 3& 3& 3& 1\\\hline & & & & 44\end{array} \Rightarrow \begin{array}{} a& b& c& d &排列數\\\hline 2 & 0 & 1& 1 &3 \\ & 0 & 1 & 2 & 6\\& 0 & 1 & 3 & 6 \\ & 0 & 2 & 2& 3\\ & 0 & 2 & 3& 6\\ &0 &3 &3 & 3\\\hdashline & 1& 1& 2 & 3\\ & 1& 1& 3& 3\\ & 1& 2& 2 & 3 \\ & 1 & 2& 3& 6\\ & 1 & 3& 3& 3\\\hdashline & 2& 2& 3& 3\\ & 2 & 3& 3& 3\\ & 3& 3& 3& 1\\\hline & & & & 52\end{array} \Rightarrow \begin{array}{} a& b& c& d &排列數\\\hline 3 & 0 & 1& 1 &3 \\ & 0 & 1 & 2 & 6\\& 0 & 1 & 3 & 6 \\ & 0 & 2 & 2& 3\\ & 0 & 2 & 3& 6\\ &0 &3 &3 & 3\\\hdashline & 1& 1& 2 & 3\\ & 1& 1& 3& 3\\ & 1& 2& 2 & 3 \\ & 1 & 2& 3& 6\\ & 1 & 3& 3& 3\\\hdashline & 2& 2& 2& 1\\ & 2& 2& 3& 3\\ & 2 & 3& 3& 3\\ & 3& 3& 3& 1\\\hline & & & & 53\end{array}\\ 1開頭有44種、2開頭有52種、3開頭有53種,共\bbox[red,2pt]{149}種千位數$$

解:$$\log (3x^3+8x^2+5x+1) = \log (2x+3) \Rightarrow \cases{3x^3+8x^2+5x+1 =2x+3\\ 3x^3+8x^2+5x+1 >0 \\2x+3>0 } \\ \Rightarrow 3x^3+8x^2+3x-2=0 \Rightarrow (x+1)(3x-1)(x+2)=0 \Rightarrow x=-1,1/3(-2不合,\because 2x+3 \not \gt 0)\\ \Rightarrow 所有實根之乘積= -1\times {1\over 3} =\bbox[red,2pt]{-1\over 3}$$

解:$$\cases{P(a,b,c) 在xy平面的投影點為(a,b,0)代入x-2y+1=0\\ P(a,b,c) 在x=y平面的投影點為((a+b)/2,(a+b)/c,c)代入x/2=y/2=(z-1)/3} \\ \Rightarrow \cases{a-2b+1=0\\ {a+b\over 4}={c-1\over 3}} \Rightarrow \cases{a=2b-1\\ c=(9b+1)/4} \Rightarrow \cases{a+1=2y\\ 4c-1=9b} \Rightarrow \bbox[red,2pt]{{x+1\over 8}={y\over 4}={z-1/4\over 9}}$$

解:
解:$$\cases{A(-9,0)\\ B(0,-4)} \Rightarrow \cases{\overleftrightarrow{AB}: 4x+9y+36=0 \\\overline{AB}= \sqrt{9^2+4^2}= \sqrt{97}}\\ {4a+{9\over a} \ge 2\sqrt{4a\cdot {9\over a}}}=12 \Rightarrow P(a,{1\over a}) \Rightarrow d(P,\overleftrightarrow{AB})= {4a+{9\over a}+36 \over \sqrt{97}} \ge {48\over \sqrt{97}} \\ \Rightarrow \triangle ABP 面積={1\over 2}\times \overline{AB}\times d(P,\overleftrightarrow{AB}) \ge {1\over 2}\times \sqrt{97}\times{48\over \sqrt{97}} =\bbox[red,2pt]{24}$$
解:$$\cases{x^3-1 = (x-1)(x^2+x+1)\\ x^3+2x^2+2x+1= (x+1) (x^2+x+1)} \\\Rightarrow f(x)=\cases{P(x)(x-1)(x^2+x+1) +ax^2-bx+1 \\ Q(x)(x+1) (x^2+x+1)-3ax^2+bx+5}\\ 令x^2+x+1=0 \Rightarrow f(x)=\cases{ax^2-bx+1 \\-3ax^2+bx+5} =\cases{a(-x-1)-bx+1 \\-3a(-x-1)+bx+5} (\because x^2=-x-1)\\=\cases{(-a-b)x-a+1 \\(3a+b)x+3a+5} \Rightarrow \cases{-a-b=3a+b\\ -a+1=3a+5} \Rightarrow (a,b)=\bbox[red,2pt]{(-1,2)}$$
解:$$S_n,a_{n+1},S_{n+1} 成等差\Rightarrow a_{n+1}-S_n =S_{n+1}-a_{n+1} \Rightarrow S_{n+1}=2a_{n+1}-S_n \Rightarrow S_{n+1} -S_n=2a_{n+1}-2S_n \\\Rightarrow a_{n+1}=2a_{n+1}-2S_n \Rightarrow a_{n+1}=2S_n\\ \Rightarrow a_2=2S_1=2a_1 \Rightarrow S_2= a_1+a_2=3a_1 \Rightarrow a_3=2S_2 = 6a_1 \Rightarrow S_3= a_3+S_2=9a_1 \\ \Rightarrow a_4=2S_3 =18a_1 \Rightarrow S_4 = a_4+S_3 =27a_1 \Rightarrow a_5=2S_4 =54a_1 =324 \Rightarrow a_1= \bbox[red,2pt]{6}$$
解:$$\begin{array}{} a& b& c& d &排列數\\\hline 1 & 0 & 1 & 2 & 6\\& 0 & 1 & 3 & 6 \\ & 0 & 2 & 2& 3\\ & 0 & 2 & 3& 6\\ &0 &3 &3 & 3\\\hdashline & 1& 2& 2 & 3 \\ & 1 & 2& 3& 6\\ & 1 & 3& 3& 3\\\hdashline & 2 & 2& 2& 1\\ & 2& 2& 3& 3\\ & 2 & 3& 3& 3\\ & 3& 3& 3& 1\\\hline & & & & 44\end{array} \Rightarrow \begin{array}{} a& b& c& d &排列數\\\hline 2 & 0 & 1& 1 &3 \\ & 0 & 1 & 2 & 6\\& 0 & 1 & 3 & 6 \\ & 0 & 2 & 2& 3\\ & 0 & 2 & 3& 6\\ &0 &3 &3 & 3\\\hdashline & 1& 1& 2 & 3\\ & 1& 1& 3& 3\\ & 1& 2& 2 & 3 \\ & 1 & 2& 3& 6\\ & 1 & 3& 3& 3\\\hdashline & 2& 2& 3& 3\\ & 2 & 3& 3& 3\\ & 3& 3& 3& 1\\\hline & & & & 52\end{array} \Rightarrow \begin{array}{} a& b& c& d &排列數\\\hline 3 & 0 & 1& 1 &3 \\ & 0 & 1 & 2 & 6\\& 0 & 1 & 3 & 6 \\ & 0 & 2 & 2& 3\\ & 0 & 2 & 3& 6\\ &0 &3 &3 & 3\\\hdashline & 1& 1& 2 & 3\\ & 1& 1& 3& 3\\ & 1& 2& 2 & 3 \\ & 1 & 2& 3& 6\\ & 1 & 3& 3& 3\\\hdashline & 2& 2& 2& 1\\ & 2& 2& 3& 3\\ & 2 & 3& 3& 3\\ & 3& 3& 3& 1\\\hline & & & & 53\end{array}\\ 1開頭有44種、2開頭有52種、3開頭有53種,共\bbox[red,2pt]{149}種千位數$$
解:$$\log (3x^3+8x^2+5x+1) = \log (2x+3) \Rightarrow \cases{3x^3+8x^2+5x+1 =2x+3\\ 3x^3+8x^2+5x+1 >0 \\2x+3>0 } \\ \Rightarrow 3x^3+8x^2+3x-2=0 \Rightarrow (x+1)(3x-1)(x+2)=0 \Rightarrow x=-1,1/3(-2不合,\because 2x+3 \not \gt 0)\\ \Rightarrow 所有實根之乘積= -1\times {1\over 3} =\bbox[red,2pt]{-1\over 3}$$
解:$$\cases{P(a,b,c) 在xy平面的投影點為(a,b,0)代入x-2y+1=0\\ P(a,b,c) 在x=y平面的投影點為((a+b)/2,(a+b)/c,c)代入x/2=y/2=(z-1)/3} \\ \Rightarrow \cases{a-2b+1=0\\ {a+b\over 4}={c-1\over 3}} \Rightarrow \cases{a=2b-1\\ c=(9b+1)/4} \Rightarrow \cases{a+1=2y\\ 4c-1=9b} \Rightarrow \bbox[red,2pt]{{x+1\over 8}={y\over 4}={z-1/4\over 9}}$$
解:
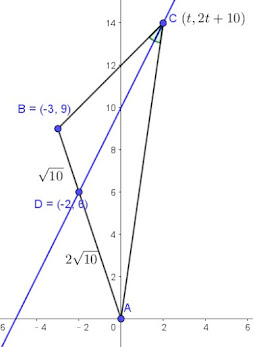
$$\cases{A(0,0)\\ B(-3,9)} \Rightarrow \overleftrightarrow{AB}: y=-3x \Rightarrow \overleftrightarrow{AB}與L的交點D(-2,6) \Rightarrow \cases{\overline{AD}=2\sqrt{10} \\\overline{BD}=\sqrt{10}} \Rightarrow \overline{AD}:\overline{BD}=2:1;\\又C在L上\Rightarrow C(t,2t+10) \Rightarrow \overline{AC}:\overline{BC}= \overline{AD}:\overline{BD}=2:1(\because L為角平分線)\\ \Rightarrow \sqrt{t^2+(2t+10)^2} =2\sqrt{(t+3)^2+(2t+1)^2} \Rightarrow 5t^2+40t+100 =20t^2+40t+40\\ \Rightarrow t^2=4 \Rightarrow t=2(t=-2 \Rightarrow C=D) \Rightarrow \bbox[red,2pt]{C(2,14)}$$

解:
解:
$$h=\cases{a\tan (90^\circ-\theta) =a/\tan\theta \cdots(1)\\(30+a)\tan 2\theta=(30+a){2\tan \theta\over 1-\tan^2\theta } \cdots(2) \\ (140+a)\tan \theta\cdots(3)}\Rightarrow \cases{(1)=(3)\\ (1)=(2)} \Rightarrow \cases{{a\over \tan \theta}=(140+a)\tan \theta \\ {a\over \tan \theta}=(30+a){2\tan \theta\over 1-\tan^2\theta }}\\ \Rightarrow \cases{{a\over 140+a}= \tan^2\theta\cdots(4)\\ {a\over 30+a}={2\tan^2 \theta \over 1-\tan^2\theta}=-2+{2\over 1-\tan^2\theta}\cdots(5)},\\將(4)代入(5) \Rightarrow {a\over 30+a}=-2+{2\over 1-(a/(140+a))} ={a\over 70} \\ \Rightarrow a=40 代入(4)\Rightarrow {40\over 180} =\tan^2 \theta \Rightarrow \tan \theta = {\sqrt 2\over 3} \Rightarrow h=(140+40)\times {\sqrt 2\over 3} =\bbox[red,2pt]{60\sqrt 2}$$
13.某中心接到其正東、 正西、 正北方向三個觀測站的報告, 正西、 正北兩地觀測站同時聽到一聲巨響, 正東觀測站聽到該巨響的時間比其他兩個觀測站晚 4 秒, 已知各觀測站到該中心的距離都是 1360 公尺, 聲音傳播速度為340 公尺/秒, 則巨響的位置到中心的距離為 ___ 公尺。
解:
$$令\cases{O:中心\\ A:正西觀測所 \\B:正北觀測所 \\C:正東觀測所 \\P:巨響位置} \Rightarrow \cases{O(0,0)\\ A(-1360,0)\\ B(0,1360) \\ C(1360,0) \\ \overline{PA}=\overline{PB}=a \\ \overline{PC}=a+340\times 4=a+1360} \Rightarrow P在\overline{AB}的中垂線上 \Rightarrow P(t,-t) \\ \Rightarrow a=\overline{PA} =\overline{PC}-1360 \Rightarrow \sqrt{(t+1360)^2+t^2} = \sqrt{(t-1360)^2+t^2}-1360 \\ \Rightarrow 2t^2+2720t+1360^2 =2t^2-2720t+1360^2 -2720\sqrt{(t-1360)^2+t^2}+1360^2\\ \Rightarrow -2t+680 = \sqrt{(t-1360)^2+t^2} \Rightarrow 4t^2-2720t+680^2=2t^2-2720t+1360^2 \\ \Rightarrow 2t^2=1360^2-680^2 =680\times (680\times 3) \Rightarrow \overline{PO}= \sqrt{2t^2} =\sqrt{680^2\times 3} =\bbox[red,2pt]{680\sqrt 3}$$

解:
解:
$${\overline{CE}\over \overline{EA}} \times{\overline{AD} \over \overline{DB}} \times{\overline{BQ}\over \overline{QC}} =1 \Rightarrow {4\over 2} \times{3 \over 1} \times{\overline{BQ}\over \overline{QC}} =1 \Rightarrow {\overline{BQ}\over \overline{QC}} ={1\over 6} \Rightarrow \cases{\overline{BQ}=a\\ \overline{QC}=6a}\\ \cases{直角\triangle AQB: \overline{QA}^2 = \overline{AB}^2-\overline{BQ}^2 =16-a^2\\ 直角\triangle AQC: \overline{QA}^2 = \overline{AC}^2-\overline{QC}^2 =36-36a^2} \Rightarrow 16-a^2=36-36a^2 \Rightarrow a^2=4/7\\ \triangle ABC: \cos \angle BAC = {4^2+6^2 -(7a)^2 \over 2\times 4\times 6} ={52-28\over 48} =\bbox[red,2pt]{1\over 2}$$
-- END (解題僅供參考) --



沒有留言:
張貼留言