110 學年度指定科目考試試題-數學乙
第壹部分:選擇題(單選題、多選題及選填題共占 74 分)
一 、單選題 (占 18 分 )
解答:
$$相關係數為正值代表年齡越大則人數越多,只有(4)符合此要;\\而(3)與(5)約一半的點是年齡越大反而人數越少,相關係數接近0,故選\bbox[red,2pt]{(4)}$$
$$令\cases{k=1\\ f(x)=\alpha x^2+\beta x+\gamma} \Rightarrow \cases{f(-1)=\alpha-\beta+\gamma =1 \\ f(1)=\alpha +\beta +\gamma = 9\\ f(3)=9\alpha+ 3\beta+\gamma =-15} \Rightarrow \cases{\alpha=-4\\ \beta=4\\ \gamma=9} \\ \Rightarrow f(x)=-4x^2+4x+9 =-4(x-{1\over 2})^2+10 \Rightarrow a={1\over 2},故選\bbox[red,2pt]{(2)}\\當然也可以不用假設k值,若a=1,則f(1-2)=f(1+2),但f(-1) \gt f(3)\\,因此極值會出現在-1與1之間$$
解答:$$和為奇數:1+2,1+4,1+6,2+3,2+5, 3+4, 3+6, 4+5,5+6,共9種情形\\ \Rightarrow 和為偶數有C^6_2-9=6種情形;因此第一次抽到兩張牌和為奇數的機率為{9\over 15}= {3\over 5},偶數為{2\over 5}\\ 第一次抽到和為偶數\Rightarrow \cases{丟掉兩張奇數牌,剩下1奇3偶\\ 丟掉兩張偶數牌,剩下3奇1偶}\\\Rightarrow 第二抽和為奇數皆是3種情形(都是奇+偶),機率為1/2\\ 期望值=100\times {3\over 5}+ 50\times {2\over 5}\times {1\over 2}=60+10=70,故選\bbox[red,2pt]{(2)}$$
解答:$$假設裝有甲和a的叫A袋,另一袋叫B袋;而d、e不同袋且每袋剛好裝4個\\(1)\bigcirc:B袋至少有d或e,剩下乙、丙、b、c要取2個,一定會取到另一個公仔,所以每袋都至少有2個公仔\\(2)\times: \cases{A=\{甲、a、c、d\}\\ B=\{乙、丙、b、e\}}\qquad 符合要求,但乙、丙皆在B袋\\(3)\times: \cases{A=\{甲、a、c、e\}\\ B=\{乙、丙、b、d\}}\qquad 符合要求,但丙、e不同袋\\(4) \times:\cases{A=\{甲、丙、a、d\}\\ B=\{乙、b、c、e\}}\qquad 符合要求,但b、c同袋\\(5)\bigcirc: b、c不同袋且d、e不同袋;因此剩下乙、丙能只都裝在B袋,才符合每袋有4個\\,故選\bbox[red,2pt]{(15)}$$
解答:$$a_{n+1}={2n+1\over 2n-1}a_n \Rightarrow a_n={2n-1\over 2n-3}a_{n-1} ={2n-1\over 2n-3}\cdot {2n-3\over 2n-5}a_{n-2} ={2n-1\over 2n-3}\cdot {2n-3\over 2n-5} \cdots {3\over 1}a_{1} = (2n-1)a_1\\ \Rightarrow a_n=(2n-1)a_1= 2n-1,n\ge 1\\(1) \bigcirc: a_2=2\cdot 2-1=3\\(2)\times: a_4=8-1=7 \\(3) \times:\langle a_n\rangle=\langle 2n-1\rangle \Rightarrow 等差數列,公差為2 \\(4) \bigcirc:\sum_{n=1}^{20}a_n =\sum_{n=1}^{20}(2n-1) = 21\times 20-20=400 \\(5) \bigcirc: \lim_{n\to\infty} {a_n\over n} =\lim_{n\to\infty} {2n-1\over n} =\lim_{n\to\infty} (2-1/n) =2\\,故選\bbox[red,2pt]{(145)}$$
解答:$$(1)\bigcirc: C^2_1{1\over 2}(1-{1\over 2})={1\over 2} \\(2)\times: C^4_2({1\over 2})^2(1-{1\over 2})^{4-2} ={6\over 16} \ne {1\over 2}\\ (3)\bigcirc: 射中1次及射中3次的機率={1\over 16}(C^4_1+C^4_3)= {8\over 16}={1\over 2} \\(4)\bigcirc: {第1次沒射中且第2次射\over 第1次沒射中} ={(1/2)\times (1/2)\over 1/2}={1\over 2} \\(5)\times: 前2次與後4次獨立,因此{前2次射中次且後4次射中2次的機率\over 前2次射中1次的機率} =4次射中2次的機率\\\qquad \quad =3/8(由(2)知)\\,故選\bbox[red,2pt]{(134)}$$
解答:$$\cases{A=\begin{bmatrix} 1& -2 \\ 0 & 1\end{bmatrix}\begin{bmatrix} 1& 0 \\ 0 & 6\end{bmatrix}\begin{bmatrix} 1& -2 \\ 0 & 1\end{bmatrix}^{-1} \\ B=\begin{bmatrix} 1& -2 \\ 0 & 1\end{bmatrix}\begin{bmatrix} 6& 0 \\ 0 & 1\end{bmatrix}\begin{bmatrix} 1& -2 \\ 0 & 1\end{bmatrix}^{-1}} \Rightarrow A+B=\begin{bmatrix} 1& -2 \\ 0 & 1\end{bmatrix} \left(\begin{bmatrix} 1& 0 \\ 0 & 6\end{bmatrix} +\begin{bmatrix} 6& 0 \\ 0 & 1\end{bmatrix}\right)\begin{bmatrix} 1& -2 \\ 0 & 1\end{bmatrix}^{-1} \\ = \begin{bmatrix} 1& -2 \\ 0 & 1\end{bmatrix} \begin{bmatrix} 7& 0 \\ 0 & 7\end{bmatrix} \begin{bmatrix} 1& -2 \\ 0 & 1\end{bmatrix}^{-1} = \begin{bmatrix} 7& -14 \\ 0 & 7\end{bmatrix} \begin{bmatrix} 1& -2 \\ 0 & 1\end{bmatrix}^{-1} = \begin{bmatrix} 7& -14 \\ 0 & 7\end{bmatrix} \begin{bmatrix} 1& 2 \\ 0 & 1\end{bmatrix} \\ =\begin{bmatrix} 7& 0 \\ 0 & 7\end{bmatrix} \Rightarrow a+b+c+d = 7+0+0+7= \bbox[red, 2pt]{14}$$
解答:$$6正0反機率=({1\over 3})^6={1\over 729}\\ 5正1反機率=C^6_5({1\over 3})^5({2\over 3})={12\over 729}\\ 4正2反機率=C^6_4({1\over 3})^4({2\over 3})^2={60\over 729}\\ 3正3反機率=C^6_3({1\over 3})^3({2\over 3})^3={160\over 729}\\ 2正4反機率=C^6_2({1\over 3})^2({2\over 3})^4={240\over 729}\\ 1正5反機率=C^6_1({1\over 3}) ({2\over 3})^5={192\over 729} \\ 0正6反機率= ({2\over 3})^6={64\over 729} \\ \Rightarrow 2正4反機率最高 \Rightarrow (0,0)+2(-1,2)+4(1,0)= \bbox[red,2pt]{(2,4)}$$
$$\cases{80x+50y \le 200\\68x+48y \le 200 \\ 1\le x,y\le 2} \Rightarrow \cases{8x+5y \le 20\\ 17x+12y \le 50\\1\le x,y\le 2} \Rightarrow 頂點坐標\cases{A(1,2)\\ B(5/4,2)\\ C(15/8,1)\\ D(1,1)},斜線區域如上圖;$$(3)$$令h(x,y)=f(x,y)-g(x,y)=12x+2y \Rightarrow \cases{h(A)=16\\ h(B)=19\\ h(C)=49/2 \\ h(D)=14}\\ 當\bbox[red,2pt]{\cases{x=15/8\\ y=1}}時,售價差距最大;此時差距為{49\over 2}=\bbox[red,2pt]{24.5萬元}$$
解答:$$和為奇數:1+2,1+4,1+6,2+3,2+5, 3+4, 3+6, 4+5,5+6,共9種情形\\ \Rightarrow 和為偶數有C^6_2-9=6種情形;因此第一次抽到兩張牌和為奇數的機率為{9\over 15}= {3\over 5},偶數為{2\over 5}\\ 第一次抽到和為偶數\Rightarrow \cases{丟掉兩張奇數牌,剩下1奇3偶\\ 丟掉兩張偶數牌,剩下3奇1偶}\\\Rightarrow 第二抽和為奇數皆是3種情形(都是奇+偶),機率為1/2\\ 期望值=100\times {3\over 5}+ 50\times {2\over 5}\times {1\over 2}=60+10=70,故選\bbox[red,2pt]{(2)}$$
二 、多選題 (占 32 分 )
解答:$$\cases{a=\log_2 8 \Rightarrow a=3\\ b=\log_3 1 \Rightarrow b=0\\ c=\log_{0.5} 8\Rightarrow c=-3} \Rightarrow \cases{(1)\bigcirc: b=0\\ (2)\times: a+b+c = 3+0-3=0 \not \gt 0 \\(3)\bigcirc: 3\gt 0\gt -3\\(4)\times: \cases{a^2=9\\ b^2=0\\ c^2=9} \Rightarrow a^2=c^2 \gt b^2\\ (5)\times: \cases{2^a=8\\ 3^b=1\\ (1/2)^c=8} \Rightarrow 2^a=(1/2)^c \gt 3^b}\\,故選\bbox[red,2pt]{(1,3)}$$解答:$$假設裝有甲和a的叫A袋,另一袋叫B袋;而d、e不同袋且每袋剛好裝4個\\(1)\bigcirc:B袋至少有d或e,剩下乙、丙、b、c要取2個,一定會取到另一個公仔,所以每袋都至少有2個公仔\\(2)\times: \cases{A=\{甲、a、c、d\}\\ B=\{乙、丙、b、e\}}\qquad 符合要求,但乙、丙皆在B袋\\(3)\times: \cases{A=\{甲、a、c、e\}\\ B=\{乙、丙、b、d\}}\qquad 符合要求,但丙、e不同袋\\(4) \times:\cases{A=\{甲、丙、a、d\}\\ B=\{乙、b、c、e\}}\qquad 符合要求,但b、c同袋\\(5)\bigcirc: b、c不同袋且d、e不同袋;因此剩下乙、丙能只都裝在B袋,才符合每袋有4個\\,故選\bbox[red,2pt]{(15)}$$
解答:$$a_{n+1}={2n+1\over 2n-1}a_n \Rightarrow a_n={2n-1\over 2n-3}a_{n-1} ={2n-1\over 2n-3}\cdot {2n-3\over 2n-5}a_{n-2} ={2n-1\over 2n-3}\cdot {2n-3\over 2n-5} \cdots {3\over 1}a_{1} = (2n-1)a_1\\ \Rightarrow a_n=(2n-1)a_1= 2n-1,n\ge 1\\(1) \bigcirc: a_2=2\cdot 2-1=3\\(2)\times: a_4=8-1=7 \\(3) \times:\langle a_n\rangle=\langle 2n-1\rangle \Rightarrow 等差數列,公差為2 \\(4) \bigcirc:\sum_{n=1}^{20}a_n =\sum_{n=1}^{20}(2n-1) = 21\times 20-20=400 \\(5) \bigcirc: \lim_{n\to\infty} {a_n\over n} =\lim_{n\to\infty} {2n-1\over n} =\lim_{n\to\infty} (2-1/n) =2\\,故選\bbox[red,2pt]{(145)}$$
解答:$$(1)\bigcirc: C^2_1{1\over 2}(1-{1\over 2})={1\over 2} \\(2)\times: C^4_2({1\over 2})^2(1-{1\over 2})^{4-2} ={6\over 16} \ne {1\over 2}\\ (3)\bigcirc: 射中1次及射中3次的機率={1\over 16}(C^4_1+C^4_3)= {8\over 16}={1\over 2} \\(4)\bigcirc: {第1次沒射中且第2次射\over 第1次沒射中} ={(1/2)\times (1/2)\over 1/2}={1\over 2} \\(5)\times: 前2次與後4次獨立,因此{前2次射中次且後4次射中2次的機率\over 前2次射中1次的機率} =4次射中2次的機率\\\qquad \quad =3/8(由(2)知)\\,故選\bbox[red,2pt]{(134)}$$
三、選填題( 占 24 分 )
解答:$$\overline{AC}\gt \overline{BC} \Rightarrow 10-{\overline{AB}\over 2}\lt x \lt 10+{\overline{AB}\over 2} \Rightarrow4\lt x\lt 16 \Rightarrow 6\lt \overline{AC} \lt 18 \cdots(1)\\ 又\overline{AC}\lt \overline{OB} \Rightarrow \overline{AC}\lt 10 \cdots(2);\\由(1)及(2) \Rightarrow 6\lt \overline{AC}\lt 10 \Rightarrow (6-2)\lt x \lt (10-2) \Rightarrow \bbox[red, 2pt]{4\lt x \lt 8}$$解答:$$\cases{A=\begin{bmatrix} 1& -2 \\ 0 & 1\end{bmatrix}\begin{bmatrix} 1& 0 \\ 0 & 6\end{bmatrix}\begin{bmatrix} 1& -2 \\ 0 & 1\end{bmatrix}^{-1} \\ B=\begin{bmatrix} 1& -2 \\ 0 & 1\end{bmatrix}\begin{bmatrix} 6& 0 \\ 0 & 1\end{bmatrix}\begin{bmatrix} 1& -2 \\ 0 & 1\end{bmatrix}^{-1}} \Rightarrow A+B=\begin{bmatrix} 1& -2 \\ 0 & 1\end{bmatrix} \left(\begin{bmatrix} 1& 0 \\ 0 & 6\end{bmatrix} +\begin{bmatrix} 6& 0 \\ 0 & 1\end{bmatrix}\right)\begin{bmatrix} 1& -2 \\ 0 & 1\end{bmatrix}^{-1} \\ = \begin{bmatrix} 1& -2 \\ 0 & 1\end{bmatrix} \begin{bmatrix} 7& 0 \\ 0 & 7\end{bmatrix} \begin{bmatrix} 1& -2 \\ 0 & 1\end{bmatrix}^{-1} = \begin{bmatrix} 7& -14 \\ 0 & 7\end{bmatrix} \begin{bmatrix} 1& -2 \\ 0 & 1\end{bmatrix}^{-1} = \begin{bmatrix} 7& -14 \\ 0 & 7\end{bmatrix} \begin{bmatrix} 1& 2 \\ 0 & 1\end{bmatrix} \\ =\begin{bmatrix} 7& 0 \\ 0 & 7\end{bmatrix} \Rightarrow a+b+c+d = 7+0+0+7= \bbox[red, 2pt]{14}$$
解答:$$6正0反機率=({1\over 3})^6={1\over 729}\\ 5正1反機率=C^6_5({1\over 3})^5({2\over 3})={12\over 729}\\ 4正2反機率=C^6_4({1\over 3})^4({2\over 3})^2={60\over 729}\\ 3正3反機率=C^6_3({1\over 3})^3({2\over 3})^3={160\over 729}\\ 2正4反機率=C^6_2({1\over 3})^2({2\over 3})^4={240\over 729}\\ 1正5反機率=C^6_1({1\over 3}) ({2\over 3})^5={192\over 729} \\ 0正6反機率= ({2\over 3})^6={64\over 729} \\ \Rightarrow 2正4反機率最高 \Rightarrow (0,0)+2(-1,2)+4(1,0)= \bbox[red,2pt]{(2,4)}$$
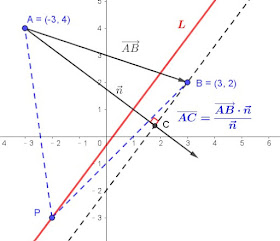
(1)$$\cases{A(-3,4)\\ B(3,2)\\ \vec n=(4,-3)} \Rightarrow \overrightarrow{AB}\cdot \vec n = (6,-2)\cdot (4,-3)=24+6=\bbox[red,2pt]{30}$$(2)$$\overrightarrow{AB}在\vec n的投影長= {\overrightarrow{AB}\cdot \vec n\over |\vec n|} ={30\over 5}=6=d(A,L)+d(B,L),又{d(A,L)\over d(B,L)}=5 \Rightarrow \cases{d(A,L)=5\\ d(B,L)=1} \\ \vec n=(4,-3) \Rightarrow L:4x-3y+k=0\Rightarrow \cases{d(A,L)=|k-24|/5=5\\ d(B,L)=|6+k|/5=1} \Rightarrow \cases{|k-24|=25\\ |k+6|=5}\\ \Rightarrow \cases{k=-1,49\\ k=-1,-11} \Rightarrow k=-1 \Rightarrow L:\bbox[red,2pt]{4x-3y=1}$$(3)$$P\in L \Rightarrow P((3t+1)/4,t),t\in \mathbb{R},由 \overline{PA}=\overline{PB}\\ \Rightarrow \left({3t+1\over 4}+3\right)^2+(t-4)^2 =\left( {3t+1\over 4}-3\right)^2 +(t-2)^2\\ \Rightarrow t=-3 \Rightarrow \bbox[red,2pt]{P(-2,-3)}$$
解答:
解答:
(1)$$\cases{甲車售價=f(x,y)=56x+26y+48\cdot (x+y)/2 \\乙車售價=g(x,y)=40x+20y+56\cdot (x+y)/2} \Rightarrow \cases{f(x,y)=80x+50y \\ g(x,y)=68x+48y} \\ \Rightarrow f(x,y)-g(x,y)=12x+2y \gt 0,1\le x\le 2,1\le y\le 2 \Rightarrow f(x,y)\gt g(x,y)\\ \Rightarrow 甲型電動車售價必高於乙型電動車的售價$$(2)
================ end ==================
















選填題C部分中間計算3正3反機率是160/729
回覆刪除謝謝指正,已修訂
刪除