國立竹北高中111學年度第1學期第1次教師甄選
填充題第一部分: 每題 6 分,共 30 分
解答:$$\cases{L_1:{x+1\over 4} ={y-3\over -1} ={z+3\over -1}\\ L_2:{x\over 4} ={y-1\over -3} ={z-6\over -2}} \Rightarrow \cases{L_1的方向向量\vec u=(4,-1,-1)\\ L_2的方向向量\vec v=(4,-3,-2)} \Rightarrow \vec n= \vec u\times \vec v=(-1,4,-8)\\ \cases{在L_1任找一點P(-1,3,-3)\\ 在L_2任找一點Q(0,1,6)} \Rightarrow \vec w=\overrightarrow{PQ}=(1,-2,9) \Rightarrow \vec w在\vec n的正射影長={|\vec w\cdot \vec n|\over |\vec n|} = {81\over \sqrt{81}}\\ =\bbox[red, 2pt]{9}$$
解答:
$$分別在\overline{AB}與\overline{CD}上找點E、F,使得\overline{DE} \bot \overline{AC}及\overline{BD} \bot\overline{AC},垂足分別是G與O,見上圖;\\ \overline{AC} =\sqrt{6^2+(2\sqrt 3)^2} =4\sqrt 3,又\overline{AB}\times \overline{BC} = \overline{AC}\times \overline{BO} \Rightarrow \overline{BO}=6\times 2\sqrt 3\div 4\sqrt 3=3\\ \Rightarrow \overline{CF} =\sqrt{(2\sqrt 3)^2-3^2} =\sqrt 3 =\overline{AG}\\ 令O為空間的原點、\overrightarrow{OB}為x軸、\overrightarrow{OA}為y軸,摺起後\cases{O(0,0,0)\\ A(0,3\sqrt 3,0)\\ B(-3\cos 30^\circ, 0,3\sin 30^\circ)=(-3\sqrt 3/2,0,3/2)\\ D(-3,2\sqrt 3,0)} \\ \Rightarrow \cases{\overrightarrow{AB} =(-3\sqrt 3/2,-3\sqrt 3,3/2)\\ \overrightarrow{AD}= (-3,-\sqrt 3,0)} \Rightarrow \cos \theta = \cfrac{9\sqrt 3/2+9}{6\times 2\sqrt 3} =\bbox[red, 2pt]{\cfrac{3+2\sqrt 3}{8}}$$
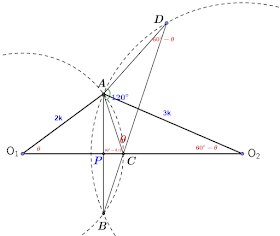
$$假設C在\overline{O_1O_2}上(可藉由調整兩圓心距離達成),\\並令\angle ACD=\theta \Rightarrow \angle ADC=180^\circ-120^\circ-\theta =60^\circ-\theta\\ \Rightarrow \angle AO_2B = 2\angle ADC (對同弧的圓心角是圓周角的2倍) \Rightarrow \angle AO_2O_1 = \angle ADC=60^\circ\\ 又\angle ACD=180^\circ-\theta \Rightarrow \angle AO_1B= 360^\circ-2(180^\circ-\theta)=2\theta \Rightarrow AO_1O_2=\theta\\ 因此\cases{\sin \angle AO_1O_2 =\sin \theta =\overline{AP}/2k\\ \sin AO_2O_1 = \sin (60^\circ-\theta) = \overline{AP}/3k} \Rightarrow \overline{AP}=2k\sin\theta =3k(\sin(60^\circ-\theta))\\ \Rightarrow 2\sin \theta = 3 ({\sqrt 3\over 2}\cos\theta -{1\over 2}\sin \theta) \Rightarrow {7\over 2}\sin \theta ={3\sqrt 3\over 2}\cos \theta \Rightarrow \tan \theta = \bbox[red, 2pt]{3\sqrt 3\over 7}$$
解答:$$令\cases{u=13x-10y+6\\ v=17x+13y-2} \Rightarrow |u|+|v|\le 339的面積=339^2\times 2\\ 而J=\begin{Vmatrix} u_x & u_y\\ v_x & v_y\end{Vmatrix} =\begin{Vmatrix} 13 & -10\\ 17 & 13\end{Vmatrix} =339 \Rightarrow 欲求之面積={339^2\times 2\over 339} =339\times 2= \bbox[red, 2pt]{678}$$
$$為什麼\overline{BG}=\overline{CF}?\\
對同弧的圓周角相等\Rightarrow \cases{\angle AFC= \angle ABG\\ \angle AGB=\angle ACF},又正\triangle 邊長相等\Rightarrow \cases{\overline{AG}= \overline{AC}\\ \overline{AF} =\overline{AB}}\\ 因此\triangle AGB \cong \triangle ACF(SAS) \Rightarrow \overline{BG} =\overline{CF}$$
$$\overline{BG}與\overline{CF}的交點P,即為費馬點,因此\overline{BG}=\overline{CF};\\再由中線定理:\cases{\triangle GBC:\overline{GC}^2 +\overline{GB}^2 = 2(\overline{GM}^2 +\overline{CM}^2) \\ \triangle FBC:\overline{FC}^2 +\overline{FB}^2 = 2(\overline{FM}^2 +\overline{CM}^2) }\\ 兩式相減\Rightarrow \overline{FB}^2-\overline{GC}^2 = \overline{AB}^2-\overline{AC}^2 = \overline{BC}^2=2(\overline{FM}^2-\overline{GM}^2) =2(11^2-7^2)=144\\ \Rightarrow \overline{BC}= \bbox[red, 2pt]{12}$$
$$為什麼\overline{BG}=\overline{CF}?\\
對同弧的圓周角相等\Rightarrow \cases{\angle AFC= \angle ABG\\ \angle AGB=\angle ACF},又正\triangle 邊長相等\Rightarrow \cases{\overline{AG}= \overline{AC}\\ \overline{AF} =\overline{AB}}\\ 因此\triangle AGB \cong \triangle ACF(SAS) \Rightarrow \overline{BG} =\overline{CF}$$
解答:$$令x={t\over 1+t}=1-{1\over 1+t},則原式變為f(x)+f({1\over x})\log(1+t)=f({1\over x})\log t+2022 \\ \Rightarrow f(x)+f({1\over x})(\log(1+t)-\log t)=2022 \Rightarrow f(x) +f({1\over x}) \log{1+t\over t} =f(x) +f({1\over x}) \log{1\over x} =2022 \\ \Rightarrow f(x) -f({1\over x}) \log{ x} =2022 \cdots(1) \\ \Rightarrow f({1\over x})-f(x)\log {1\over x}=2022 \Rightarrow f({1\over x})+f(x)\log x=2022 \Rightarrow f({1\over x}) \log{ x} +f(x)(\log x)^2= 2022\log x \\ \Rightarrow f({1\over x}) \log{ x} =2022\log x-f(x)(\log x)^2代入(1) \Rightarrow f(x)-2022\log x+f(x)(\log x)^2=2022\\ \Rightarrow f(x) = {2022(1+\log x)\over 1+(\log x)^2} \Rightarrow f(1000)= {2022\cdot 4\over 1+9} = \bbox[red, 2pt]{808.8}$$
解答:$$a_n= \sqrt{1+a_{n-1}\over 2} \Rightarrow 2a_n^2-1=a_{n-1}此算式與2\cos^2\theta-1 = \cos 2\theta一致;\\ 因此a_0= {\sqrt 3\over 2} =\cos {\pi\over 6} \Rightarrow a_1= \cos{\pi\over 12} \Rightarrow a_n= \cos{\pi \over 6\cdot 2^n} \Rightarrow 4^n(1-a_n) =4^n(1- \cos{\pi \over 6\cdot 2^n})\\ 由於\cos x=1-{1\over 2}x^2 +{1\over 4!}x^4-{1\over 6!}x^6+ \cdots,因此1- \cos{\pi \over 6\cdot 2^n} ={1\over 2}({\pi \over 6\cdot 2^n})^2-{1\over 4!}({\pi \over 6\cdot 2^n})^4+\cdots \\ \Rightarrow 4^n(1- \cos{\pi \over 6\cdot 2^n}) ={\pi^2\over 72} -{4^n\over 4!}({\pi \over 6\cdot 2^n})^4+\cdots \Rightarrow \lim_{n\to \infty} 4^n(1-a_n) ={\pi^2\over 72}-0+0-\cdots =\bbox[red, 2pt]{\pi^2\over 72}$$
解答:$$可重複選取,共有4^3=64種組合,但需扣除非直線及重複的直線,如下:\\ \begin{array}{} a & b& c& 說明\\\hline 0 & 0 & 0 & 非直線\\ 0 & 0 & 1\\ 0 & 0 & 2\\ 0 & 0 & 3\\\hdashline 0 & 1 & 1& y=1\\ 0 & 2 & 2\\ 0 & 3 & 3\\\hdashline 1 & 0 & 1 & x=1\\ 2 & 0 & 2\\ 3 & 0 & 3\\\hdashline 1 & 1 & 0 & x+y=0\\ 2 & 2& 0 \\ 3 & 3 & 0\\\hdashline 1 & 1 & 1& x+y=1\\ 2 & 2& 2 \\ 3 & 3& 3\\\hdashline 1 & 0 & 0 & x=0\\ 2& 0 & 0\\ 3 & 0 & 0\\\hdashline 0 & 1& 0 & y=0\\ 0 & 2 & 0 \\ 0 & 3 & 0\\\hline\end{array} \Rightarrow 需扣除4 + 6\times 2=16,因此有64-16=\bbox[red, 2pt]{48}不同的直線$$
解答:
解答:$$a_n= \sqrt{1+a_{n-1}\over 2} \Rightarrow 2a_n^2-1=a_{n-1}此算式與2\cos^2\theta-1 = \cos 2\theta一致;\\ 因此a_0= {\sqrt 3\over 2} =\cos {\pi\over 6} \Rightarrow a_1= \cos{\pi\over 12} \Rightarrow a_n= \cos{\pi \over 6\cdot 2^n} \Rightarrow 4^n(1-a_n) =4^n(1- \cos{\pi \over 6\cdot 2^n})\\ 由於\cos x=1-{1\over 2}x^2 +{1\over 4!}x^4-{1\over 6!}x^6+ \cdots,因此1- \cos{\pi \over 6\cdot 2^n} ={1\over 2}({\pi \over 6\cdot 2^n})^2-{1\over 4!}({\pi \over 6\cdot 2^n})^4+\cdots \\ \Rightarrow 4^n(1- \cos{\pi \over 6\cdot 2^n}) ={\pi^2\over 72} -{4^n\over 4!}({\pi \over 6\cdot 2^n})^4+\cdots \Rightarrow \lim_{n\to \infty} 4^n(1-a_n) ={\pi^2\over 72}-0+0-\cdots =\bbox[red, 2pt]{\pi^2\over 72}$$
解答:$$可重複選取,共有4^3=64種組合,但需扣除非直線及重複的直線,如下:\\ \begin{array}{} a & b& c& 說明\\\hline 0 & 0 & 0 & 非直線\\ 0 & 0 & 1\\ 0 & 0 & 2\\ 0 & 0 & 3\\\hdashline 0 & 1 & 1& y=1\\ 0 & 2 & 2\\ 0 & 3 & 3\\\hdashline 1 & 0 & 1 & x=1\\ 2 & 0 & 2\\ 3 & 0 & 3\\\hdashline 1 & 1 & 0 & x+y=0\\ 2 & 2& 0 \\ 3 & 3 & 0\\\hdashline 1 & 1 & 1& x+y=1\\ 2 & 2& 2 \\ 3 & 3& 3\\\hdashline 1 & 0 & 0 & x=0\\ 2& 0 & 0\\ 3 & 0 & 0\\\hdashline 0 & 1& 0 & y=0\\ 0 & 2 & 0 \\ 0 & 3 & 0\\\hline\end{array} \Rightarrow 需扣除4 + 6\times 2=16,因此有64-16=\bbox[red, 2pt]{48}不同的直線$$
解答:
$$\cases{g(3-2i)=0 \\ \deg(g)=2}\Rightarrow g(x)=a(x-(3-2i))(x-(3+2i)) = a(x^2-6x+13),\\又g(0)=26 \Rightarrow 13a=26\Rightarrow a=2 \Rightarrow g(x)= 2(x^2-6x+13)\\ \cases{f(3-2i)=0\\ \deg(f)=3} \Rightarrow f(x)= (x^2-6x+13)(bx+c),又\cases{f(0)=13 \\ f(1)=16} \Rightarrow \cases{13c=13 \\ 8(b+c)=16} \\ \Rightarrow \cases{b=1\\ c=1} \Rightarrow f(x)=(x^2-6x+13)(x+1)\\ f(x)=g(x) \Rightarrow x+1=2 \Rightarrow x=1 \Rightarrow P=(1,g(1))= (1,16);\\ f'(x)= (2x-6)(x+1)+ (x^2-6x+13) \Rightarrow f'(1)= -8+8=0 \Rightarrow 切線L為一水平線:y=16 \\ \Rightarrow \cases{ L\cap (y=f(x)) \Rightarrow (x^2-6x+13)(x+1)=16 \Rightarrow x=1,3\\ L\cap (y=g(x)) \Rightarrow 2(x^2-6x+13)=16 \Rightarrow x=1,5} \\ \Rightarrow {F\over G} =\cfrac{\int_1^3 16-f(x)\,dx}{\int_1^5 16-g(x)\,dx} =\cfrac{4/3}{64/3} = \bbox[red, 2pt]{1\over 16}$$
解答:$$令\cases{z_1= a+ 2ai\\ z_2= \cos(-\theta) +i\sin (-\theta)} \Rightarrow \cases{P(z_1)的軌跡為一直線:y=2x\\ Q(z_2) 的軌跡為一單位圓,且圓心在原點,即x^2+y^2=1} \\\Rightarrow z= (a+\cos\theta) +(2a-\sin\theta)i = z_1+z_2 \Rightarrow |z|= |z_1+z_2 | \le 2\\ 因此直線與單位圓的交點(\pm {1\over \sqrt 5},\pm {2\over \sqrt 5})就是線段的界限,即\bbox[red, 2pt]{-{1\over \sqrt 5} \le a\le {1\over \sqrt 5}}才符合|z|\le 2$$
解答:$$第一個a有16個位置可填,第2個a只能填剩下的9個位置,因此有16\times 9=144種填法\\,但兩個a長的一樣,所以有144\div 2=72種填法;同理,2個b也有72種填法;\\若不考慮重複問題,兩個a兩個b有72^2種填法;若兩個a與兩個b剛好填在相同位置,則有72種;\\ 若一個a與一個b剛好填在相同位置,另一個a與另一個b不再同位置,則有16\times 9\times 8=1152種;\\綜合以上,符合要求的填法共有72^2-72-1152= \bbox[red,2pt]{3960}種$$
解答:
解答:$$第一個a有16個位置可填,第2個a只能填剩下的9個位置,因此有16\times 9=144種填法\\,但兩個a長的一樣,所以有144\div 2=72種填法;同理,2個b也有72種填法;\\若不考慮重複問題,兩個a兩個b有72^2種填法;若兩個a與兩個b剛好填在相同位置,則有72種;\\ 若一個a與一個b剛好填在相同位置,另一個a與另一個b不再同位置,則有16\times 9\times 8=1152種;\\綜合以上,符合要求的填法共有72^2-72-1152= \bbox[red,2pt]{3960}種$$
解答:
$$假設A、B在準線L的投影點分別為A'及B',則\overline{MN}為梯形AA'B'B的中線;\\依拋物線定義\cases{\overline{AA'}= \overline{AF}=a\\ \overline{BB'} = \overline{BF}= b},則中線長\overline{MN}= (a+b)/2;\\餘弦定理:\cos 60^\circ {1\over 2}={a^2+b^2-\overline{AB}^2 \over 2ab} \Rightarrow \overline{AB}^2 = a^2+b^2-ab \\\Rightarrow {\overline{MN} \over \overline{AB}} ={(a+b)/2\over \sqrt{a^2+b^2-ab}} ={a+b\over 2\sqrt{(a+b)^2-3ab}}\\ ={1\over 2\sqrt{1-{3ab\over (a+b)^2}}}\le {1\over 2\sqrt{1-{3ab\over 4ab}}}=1(\because a+b\ge 2\sqrt{ab} \Rightarrow (a+b)^2 \ge 4ab) \\ \Rightarrow {\overline{MN} \over \overline{AB}} 最大值=\bbox[red, 2pt]{1}$$
解答:$$\begin{array}{c|cccccc|r}i &1 & 2 & 3 & 4 & 5 & 6 & \sum\\ \hline x_i &15 & 9 & 10 & x_4 & 12 & 6 & 52+x_4\\ y_i & 12 & 10 & 7 & 7 & y_5 & y_6 & 36+ y_5+y_6\\\hdashline x_i^2 & 225 & 81 & 100 & x_4^2 & 144 & 36 & 586+x_4^2\\y_i^2 & 144 & 100 & 49 & 49 & y_5^2 & y_6^2 & 342+y_5^2 +y_6^2\\x_i y_i & 180 & 90 & 70 & 7x_4 & 12y_5 & 6y_6 & 340+7x_4 +12y_5+ 6y_6\end{array}\\ \bar x=10={1\over 6} \sum x_i \Rightarrow 60 =52+x_4 \Rightarrow x_4=8 \Rightarrow \sum x_i^2 = 586+8^2
= 650\\ \bar y= 8 ={1\over 6}\sum y_i \Rightarrow 48 = 36+y_5+y_6 \Rightarrow y_5+y_6 = 12;\\ Var(Y)={16\over 3} = EY^2 -(EY)^2 = (342+y_5^2+y_6^2)/6-8^2 \Rightarrow y_5^2 +y_6^2= 74\\ 由\cases{y_5+y_6=12 \\ y_5^2+y_6^2 =74} \Rightarrow (y_5,y_6) =(7,5) (題意:y_5\gt y_6)\\\Rightarrow 相關係數r=\cfrac{\sum (x_iy_i)-(\sum x_i)(\sum y_i)/n}{\sqrt{\sum x_i^2-(\sum x_i)^2/n} \cdot \sqrt{\sum y_i^2-(\sum y_i)^2/n}} \\= \cfrac{396+12\cdot 7+6\cdot 5-60\cdot 48/6}{\sqrt{650-60^2/6}\cdot \sqrt{416-48^2/6}} ={30\over 5\sqrt 2\cdot 4\sqrt 2}={3\over 4}\\ 迴歸直線斜率m=\cfrac{\sum (x_iy_i)-(\sum x_i)(\sum y_i)/n}{ {\sum x_i^2-(\sum x_i)^2/n} } ={30\over (5\sqrt 2)^2} ={3\over 5}\\ \Rightarrow (r,m)= \bbox[red, 2pt]{({3\over 4},{3\over 5})}$$
解答:$$f(x)=\sum_{k=1}^{10}x^k = x+ x^2+\cdots + x^{10}={x-x^{11}\over 1-x} \Rightarrow f'(x)=1+2x+ 3x^2+\cdots +10x^9 \\={1-11x^{10}\over 1-x} +{x-x^{11}\over (1-x)^2} \Rightarrow xf'(x)= \sum_{k=1}^{10}kx^k = {x-11x^{11}\over 1-x} +{x^2-x^{12}\over (1-x)^2} ={x-11x^{11}+ 10x^{12}\over (1-x)^2}\\{1\over 5}+ {4\over 5^2} +{7\over 5^3}+\cdots +{28\over 5^{10}} =\sum_{k=1}^{10} {3k-2\over 5^k} =3\sum_{k=1}^{10} {k\over 5^k}-2\sum_{k=1}^{10}{1\over 5^k}\\ =3\cdot {(1/5)-11/5^{11}+10/5^{12}\over (1-1/5)^2}-2\cdot {1/5-1/5^{11}\over 1-1/5} = {1/5+2/5^2-31/5^{11}+ 28/5^{12}\over 16/25} \\={7-31/5^9+28/5^{10}\over 16} =\cfrac{7+(-127)\times{1\over 5^{10}}}{16} \Rightarrow \cases{p=7\\ q=-127\\ r=16} \Rightarrow p+q+r =7-127+16= \bbox[red,2pt]{-104}$$
= 650\\ \bar y= 8 ={1\over 6}\sum y_i \Rightarrow 48 = 36+y_5+y_6 \Rightarrow y_5+y_6 = 12;\\ Var(Y)={16\over 3} = EY^2 -(EY)^2 = (342+y_5^2+y_6^2)/6-8^2 \Rightarrow y_5^2 +y_6^2= 74\\ 由\cases{y_5+y_6=12 \\ y_5^2+y_6^2 =74} \Rightarrow (y_5,y_6) =(7,5) (題意:y_5\gt y_6)\\\Rightarrow 相關係數r=\cfrac{\sum (x_iy_i)-(\sum x_i)(\sum y_i)/n}{\sqrt{\sum x_i^2-(\sum x_i)^2/n} \cdot \sqrt{\sum y_i^2-(\sum y_i)^2/n}} \\= \cfrac{396+12\cdot 7+6\cdot 5-60\cdot 48/6}{\sqrt{650-60^2/6}\cdot \sqrt{416-48^2/6}} ={30\over 5\sqrt 2\cdot 4\sqrt 2}={3\over 4}\\ 迴歸直線斜率m=\cfrac{\sum (x_iy_i)-(\sum x_i)(\sum y_i)/n}{ {\sum x_i^2-(\sum x_i)^2/n} } ={30\over (5\sqrt 2)^2} ={3\over 5}\\ \Rightarrow (r,m)= \bbox[red, 2pt]{({3\over 4},{3\over 5})}$$
解答:$$f(x)=\sum_{k=1}^{10}x^k = x+ x^2+\cdots + x^{10}={x-x^{11}\over 1-x} \Rightarrow f'(x)=1+2x+ 3x^2+\cdots +10x^9 \\={1-11x^{10}\over 1-x} +{x-x^{11}\over (1-x)^2} \Rightarrow xf'(x)= \sum_{k=1}^{10}kx^k = {x-11x^{11}\over 1-x} +{x^2-x^{12}\over (1-x)^2} ={x-11x^{11}+ 10x^{12}\over (1-x)^2}\\{1\over 5}+ {4\over 5^2} +{7\over 5^3}+\cdots +{28\over 5^{10}} =\sum_{k=1}^{10} {3k-2\over 5^k} =3\sum_{k=1}^{10} {k\over 5^k}-2\sum_{k=1}^{10}{1\over 5^k}\\ =3\cdot {(1/5)-11/5^{11}+10/5^{12}\over (1-1/5)^2}-2\cdot {1/5-1/5^{11}\over 1-1/5} = {1/5+2/5^2-31/5^{11}+ 28/5^{12}\over 16/25} \\={7-31/5^9+28/5^{10}\over 16} =\cfrac{7+(-127)\times{1\over 5^{10}}}{16} \Rightarrow \cases{p=7\\ q=-127\\ r=16} \Rightarrow p+q+r =7-127+16= \bbox[red,2pt]{-104}$$
======================== END ==============================










沒有留言:
張貼留言