臺北市立技術型高中暨進修部111 學年度聯合轉學考招生考試
升高二數學科試題(技高)
一、 單選題:
解答:$$判別式\lt 0 \Rightarrow a^2-3\lt 0 \Rightarrow -\sqrt 3\lt a\lt \sqrt 3,故選\bbox[red, 2pt]{(A)}$$解答:$$P=(3A+2B)\div 5 \Rightarrow P的x坐標={51+84\over 197\cdot 5} ={27\over 917},故選\bbox[red, 2pt]{(B)}$$
解答:$$\cases{x\ge 1+\sqrt 5 \\ x\le 1-\sqrt 5 }\Rightarrow \cases{x-1\ge \sqrt 5 \\ x-1\le -\sqrt 5} \Rightarrow |x-1|\ge \sqrt 5,故選\bbox[red, 2pt]{(C)}$$
解答:$$只有\overline{DE}與\overline{AB}的斜率是負值,而\overline{AB}較陡,故選\bbox[red, 2pt]{(A)}$$
解答:$$3x+4y-12=0\Rightarrow \cases{與x軸交於A(4,0)\\ 與y軸交於B(0,3)} \Rightarrow \cases{a=-3/4\\ b=4\\ c=3\\ d=3\times 4\div 2=6} \\ \Rightarrow ab+cd = -3+18=15,故選\bbox[red, 2pt]{(D)}$$
解答:$$f(x)=x^3+mx^2+nx-2 = (x+1)(x-2)p(x) \Rightarrow \cases{f(-1)=m-n-3=0 \\ f(2)=4m+2n=-6} \Rightarrow \cases{m=0\\ n=-3} \\ \Rightarrow 2m+n=0-3=-3,故選\bbox[red, 2pt]{(A)}$$
解答:$$100\times(-3)^4 +250\times(-3)^3-100\times (-3)^2+140\times(-3)-20 \\= (-3)^3 (-300+250)-100\times (-3)^2+140\times(-3)-20 \\=-50\times(-3)^3 -100\times (-3)^2+140\times(-3)-20 = (-3)^2(150-100) 140\times(-3)-20 \\=50\times(-3)^2+140\times(-3)-20 = (-3)(-150+140)-20 =30-20=10,故選\bbox[red, 2pt]{(B)}$$
解答:$$\cases{A(4,0)\\ B(0,-3) } \Rightarrow 直線L=\overleftrightarrow{AB}:3x-4y-12=0 \\ \Rightarrow (-5,2)至L距離={|-15-8-12|\over \sqrt{3^2+4^2}} ={35\over 5}=7,故選\bbox[red, 2pt]{(A)}$$
解答:$$\sin \pi +\cos \pi=0-1=-1 \Rightarrow (\pi,-1)在圖形上,(\pi ,1)不在圖形上,故選\bbox[red, 2pt]{(D)}$$
解答:$$f(x)=-\cos^2x-4\cos x+3 =-(\cos^2x+4\cos x+4)+7=-(\cos x+2)^2+7\\ \Rightarrow \cases{最大值=f(\pi)=6\\ 最小值=f(0)=-2} \Rightarrow 6-2=4,故選\bbox[red, 2pt]{(C)}$$
解答:$$分針走了{3\over 4}的圓,面積為{3\over 4}\times 12^2\pi =96\pi,故選\bbox[red, 2pt]{(B)}$$
解答:$$x=\pi \Rightarrow y=1 \Rightarrow -\cos(\pi)=1,故選\bbox[red, 2pt]{(D)}$$
解答:
$$假設O為圓心\Rightarrow \angle BOC=2\angle A=60^\circ \Rightarrow \triangle OAB為正三角形\Rightarrow 圓半徑r=\overline{BC}=10\\ 同理:\angle EOF=2\angle D=90^\circ \Rightarrow \overline{EF}^2=r^2+r^2=200 \Rightarrow \overline{EF}=10\sqrt 2,故選\bbox[red, 2pt]{(A)}$$
解答:$$\cases{A(-3,-2) \\B(1,0)} \Rightarrow \cases{直徑\overline{AB}=2\sqrt 5 \Rightarrow 半徑r=\sqrt 5\\ 圓心O=(A+B)\div 2= (-1,-1)} \\ \Rightarrow 圓方程式:(x+1)^2+(y+1)^2=5,故選\bbox[red, 2pt]{(D)}$$
解答:$$x^2+y^2-4x+2y-8=0 \Rightarrow (x-2)^2+(y+1)^2=13 \Rightarrow 圓心O(2,-1) \\ \Rightarrow \overline{OP} 斜率={3\over 2} \Rightarrow 切線斜率=-{2\over 3} \Rightarrow 過P(4,2)且斜率為-{2\over 3}的切線方程式:y=-{2\over 3}(x-4)+2 \\ \Rightarrow 2x+3y=14,故選\bbox[red, 2pt]{(B)}$$
解答:$$\cases{\overrightarrow{PQ} =(3,-4)\\ P(5,1)\\ Q(x,y)} \Rightarrow \overrightarrow{PQ} =(x-5,y-1) =(3,-4) \Rightarrow \cases{x=8\\ y=-3} \Rightarrow Q(8,-3),故選\bbox[red, 2pt]{(C)}$$
解答:$$\overrightarrow{BA} +\overrightarrow{AD} +\overrightarrow{DB} =0 \Rightarrow -\vec a+\vec b+2\overrightarrow{OB}=0 \Rightarrow \overrightarrow{OB}={1\over 2}(\vec a-\vec b) \Rightarrow y=-{1\over 2},故選\bbox[red, 2pt]{(D)}$$
解答:$$\cases{3\alpha-\beta+6=0 \\ 2\alpha+\beta-1=0} \Rightarrow \cases{\alpha=-1 \\\beta =3} \Rightarrow \alpha+\beta=2,故選\bbox[red, 2pt]{(C)}$$
解答:$$假設\cases{A(0,0)\\ C(6,0) \\B(3,3\sqrt 3)} \Rightarrow \cases{\overrightarrow{CA}=(-6,0)\\ \overrightarrow{AB}=(3,3\sqrt 3)} \Rightarrow \overrightarrow{CA} \cdot\overrightarrow{AB}= -18,故選\bbox[red, 2pt]{(B)}$$
解答:$${x\over x-1}+{3\over x-2} ={x(x-2)+3(x-1) \over (x-1)(x-2)} ={x^2+x-3\over x^2-3x+2} ={ x+1\over x^2-3x+2} \\ \Rightarrow x^2+x-3=x+1 \Rightarrow x^2=4 \Rightarrow x=-2(x-2在分母,因此x\ne 2),故選\bbox[red, 2pt]{(A)}$$
解答:$$4x^2+4x+1=(2x+1)^2\gt 0 \Rightarrow 只要x\ne -{1\over 2},其它任意數皆可,故選\bbox[red, 2pt]{(B)}$$
解答:$$2916=4\times 3^{n-1} \Rightarrow 3^{n-1} =729 =3^6 \Rightarrow n=7,故選\bbox[red, 2pt]{(C)}$$
解答:$$18+(x-4)=2\times (x+6) \Rightarrow x=2,故選\bbox[red, 2pt]{(C)}$$
解答:$$S= (-1)+{1\over 2}+(-{1\over 4}) +\cdots +{1\over 2^7} \\\Rightarrow -{1\over 2}S={1\over 2}-{1\over 4}+{1\over 8}+ \cdots -{1\over 2^8} \\ \Rightarrow S-(-{1\over 2})S =-1+{1\over 2^8} \Rightarrow {3\over 2}S=-{255\over 256} \Rightarrow S=-{85\over 128},故選\bbox[red, 2pt]{(D)}$$
解答:$$a_n=a_{n-1}+3 \Rightarrow a_n 為等差數列 \Rightarrow a_{50}=4+49\times 3=151,故選\bbox[red, 2pt]{(D)}$$
解答:$$\cases{A(-3,-2) \\B(1,0)} \Rightarrow \cases{直徑\overline{AB}=2\sqrt 5 \Rightarrow 半徑r=\sqrt 5\\ 圓心O=(A+B)\div 2= (-1,-1)} \\ \Rightarrow 圓方程式:(x+1)^2+(y+1)^2=5,故選\bbox[red, 2pt]{(D)}$$
解答:$$x^2+y^2-4x+2y-8=0 \Rightarrow (x-2)^2+(y+1)^2=13 \Rightarrow 圓心O(2,-1) \\ \Rightarrow \overline{OP} 斜率={3\over 2} \Rightarrow 切線斜率=-{2\over 3} \Rightarrow 過P(4,2)且斜率為-{2\over 3}的切線方程式:y=-{2\over 3}(x-4)+2 \\ \Rightarrow 2x+3y=14,故選\bbox[red, 2pt]{(B)}$$
解答:$$\cases{\overrightarrow{PQ} =(3,-4)\\ P(5,1)\\ Q(x,y)} \Rightarrow \overrightarrow{PQ} =(x-5,y-1) =(3,-4) \Rightarrow \cases{x=8\\ y=-3} \Rightarrow Q(8,-3),故選\bbox[red, 2pt]{(C)}$$
解答:$$\overrightarrow{BA} +\overrightarrow{AD} +\overrightarrow{DB} =0 \Rightarrow -\vec a+\vec b+2\overrightarrow{OB}=0 \Rightarrow \overrightarrow{OB}={1\over 2}(\vec a-\vec b) \Rightarrow y=-{1\over 2},故選\bbox[red, 2pt]{(D)}$$
解答:$$\cases{3\alpha-\beta+6=0 \\ 2\alpha+\beta-1=0} \Rightarrow \cases{\alpha=-1 \\\beta =3} \Rightarrow \alpha+\beta=2,故選\bbox[red, 2pt]{(C)}$$
解答:$$假設\cases{A(0,0)\\ C(6,0) \\B(3,3\sqrt 3)} \Rightarrow \cases{\overrightarrow{CA}=(-6,0)\\ \overrightarrow{AB}=(3,3\sqrt 3)} \Rightarrow \overrightarrow{CA} \cdot\overrightarrow{AB}= -18,故選\bbox[red, 2pt]{(B)}$$
解答:$${x\over x-1}+{3\over x-2} ={x(x-2)+3(x-1) \over (x-1)(x-2)} ={x^2+x-3\over x^2-3x+2} ={ x+1\over x^2-3x+2} \\ \Rightarrow x^2+x-3=x+1 \Rightarrow x^2=4 \Rightarrow x=-2(x-2在分母,因此x\ne 2),故選\bbox[red, 2pt]{(A)}$$
解答:$$4x^2+4x+1=(2x+1)^2\gt 0 \Rightarrow 只要x\ne -{1\over 2},其它任意數皆可,故選\bbox[red, 2pt]{(B)}$$
解答:$$2916=4\times 3^{n-1} \Rightarrow 3^{n-1} =729 =3^6 \Rightarrow n=7,故選\bbox[red, 2pt]{(C)}$$
解答:$$18+(x-4)=2\times (x+6) \Rightarrow x=2,故選\bbox[red, 2pt]{(C)}$$
解答:$$S= (-1)+{1\over 2}+(-{1\over 4}) +\cdots +{1\over 2^7} \\\Rightarrow -{1\over 2}S={1\over 2}-{1\over 4}+{1\over 8}+ \cdots -{1\over 2^8} \\ \Rightarrow S-(-{1\over 2})S =-1+{1\over 2^8} \Rightarrow {3\over 2}S=-{255\over 256} \Rightarrow S=-{85\over 128},故選\bbox[red, 2pt]{(D)}$$
解答:$$a_n=a_{n-1}+3 \Rightarrow a_n 為等差數列 \Rightarrow a_{50}=4+49\times 3=151,故選\bbox[red, 2pt]{(D)}$$
============================ END =============================
解題僅供參考,其他轉學考試題及詳解


















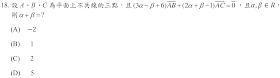









沒有留言:
張貼留言