113年中山機電碩士班-工程數學詳解

 國立中山大學113學年度碩士班招生考試

科目名稱:工程數學【機電系碩士班乙組、丙組】

解答: $$\textbf{(a)}\; y=x^m \Rightarrow y'=mx^{m-1} \Rightarrow y''=m(m-1)x^{m-2} \\ \quad \Rightarrow x^2y''-2xy'+4y= (m^2-3m+4)x^m =0 \Rightarrow m^2-3m+4=0 \Rightarrow m={3\pm \sqrt 7 i\over 2} \\ \quad \Rightarrow y_h=c_1 x^{3/2} \cos\left({\sqrt 7\over 2}\ln x \right) +c_2 x^{3/2} \sin\left({\sqrt 7\over 2}\ln x \right) ..\bbox[cyan,2pt]{待解}\\\textbf{(b)}\; y=x顯然為其一解,因此令\cases{y_1=x\\ y =v+y_1=v+x}代回原式 \\\Rightarrow x(v'+1)-(v+x)+2(v+x)^2=2x^2 \Rightarrow xv'-v+2v^2+4xv=0 \Rightarrow v'+(4-{1\over x})v=-{2\over x}v^2\\ 取u={1\over v} \Rightarrow u'=-{v'\over v^2}=-u^2v' \Rightarrow v'=-{u'\over u^2} \Rightarrow -{u'\over u^2}+(4-{1\over x}){1\over u}=-{2\over x}\cdot {1\over u^2} \\ \Rightarrow u'+({1\over x}-4)u={2\over x} \Rightarrow \text{ integrating factor }I(x)=e^{\int ((1/x)-4)\,dx} =xe^{-4x} \\ \Rightarrow xe^{-4x}u'+(1-4x)e^{-4x}u=2e^{-4x} \Rightarrow \left( x e^{-4x} u\right)'=2e^{-4x} \Rightarrow xe^{-4x}u= \int 2e^{-4x}\,dx =-{1\over 2}e^{-4x}+c_1 \\ \Rightarrow u=-{1\over 2x}+{c_1\over x}e^{4x} ={c_2e^{4x} -1\over 2x} \Rightarrow v={1\over u} ={2x\over c_2e^{4x}-1} \Rightarrow y=v+x \\ \Rightarrow \bbox[red, 2pt]{y={2x\over c_2e^{4x}-1}+x}$$

解答: (a)

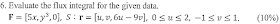
$$\mathbf{(b)}\; \bbox[red, 2pt]{f(t)= {\pi\over 3}(u(t)-u(t-2\pi)) + u(t-4\pi) 2\pi \sin(4t)} \\\mathbf{(c)}\; L\{f(t)\} =\int_0^\infty f(t)e^{-st}\,dt = \int_0^{2\pi} {\pi\over 3}e^{-st}\,dt +\int_{4\pi}^\infty 2\pi \sin(4t) e^{-st}\,dt \\\quad ={\pi\over 3}\left. \left[-{1\over s}e^{-st} \right] \right|_0^{2\pi}+ 2\pi\left. \left[ -{e^{-st}\over s^2+16}(s \sin(4t)+ 4\cos(4t) \right] \right|_0^{\infty} \\\quad =  \bbox[red, 2pt]{{\pi\over 3s} \left(1-e^{-2\pi s} \right) +2\pi\left( {4\over s^2+16}\right)}$$

解答: $$\mathbf{(a)}\;A= \left[\begin{matrix}1 & 0 & -2 & -1\\2 & 1 & -3 & 1\\-2 & 4 & 1 & 2\\0 & 2 & 0 & 2\end{matrix}\right] \xrightarrow{R_2-2R_1\to R_2,R_3+2R_1\to R_3} \left[\begin{matrix}1 & 0 & -2 & -1\\0 & 1 & 1 & 3\\0 & 4 & -3 & 0\\0 & 2 & 0 & 2\end{matrix}\right] \xrightarrow{R_3-4R_2\to R_3, R_4-2R_2\to R_4} \\ \left[\begin{matrix}1 & 0 & -2 & -1\\0 & 1 & 1 & 3\\0 & 0 & -7 & -12\\0 & 0 & -2 & -4\end{matrix}\right] \xrightarrow{R_3/(-7) \to R_3} \left[\begin{matrix}1 & 0 & -2 & -1\\0 & 1 & 1 & 3\\0 & 0 & 1 & \frac{12}{7}\\0 & 0 & -2 & -4\end{matrix}\right] \xrightarrow{R_1+2R_3\to R_1,R_2-R_3 \to R_2, R_4+2R_3\to R_4} \\\left[\begin{matrix}1 & 0 & 0 & \frac{17}{7}\\0 & 1 & 0 & \frac{9}{7}\\0 & 0 & 1 & \frac{12}{7}\\0 & 0 & 0 & - \frac{4}{7}\end{matrix}\right] \xrightarrow{-(7/4)R_4 \to R_4} \left[\begin{matrix}1 & 0 & 0 & \frac{17}{7}\\0 & 1 & 0 & \frac{9}{7}\\0 & 0 & 1 & \frac{12}{7}\\0 & 0 & 0 & 1\end{matrix}\right] \xrightarrow {R_1-(17/7)R_4\to R_1, RO2-(9/7)R_4\to R_2, R_3-(12/7)R_4\to R_3} \\ \left[\begin{matrix}1 & 0 & 0 & 0\\0 & 1& 0 & 0\\0 & 0 & 1& 0\\ 0 & 0 & 0 & 1\end{matrix}\right] \Rightarrow rref(A)=  \left[\begin{matrix}1 & 0 & 0 & 0\\0 & 1& 0 & 0\\0 & 0 & 1& 0\\ 0 & 0 & 0 & 1\end{matrix}\right] \Rightarrow rank(A)=\bbox[red, 2pt] 4 \\ \mathbf{(b)}\;A= \left[\begin{matrix}1 & 0 & -2 & -1\\2 & 1 & -3 & 1\\-2 & 4 & 1 & 2\\0 & 2 & 0 & 2\end{matrix}\right] \xrightarrow{R_2-2R_1\to R_2,R_3+2R_1\to R_3} \left[\begin{matrix}1 & 0 & -2 & -1\\0 & 1 & 1 & 3\\0 & 4 & -3 & 0\\0 & 2 & 0 & 2\end{matrix}\right] \xrightarrow{R_3-4R_2\to R_3, R_4-2R_2\to R_4} \\ \left[\begin{matrix}1 & 0 & -2 & -1\\0 & 1 & 1 & 3\\0 & 0 & -7 & -12\\0 & 0 & -2 & -4\end{matrix}\right] \xrightarrow{R_4-(2/7)R_3\to R_4} \left[\begin{matrix}1 & 0 & -2 & -1\\0 & 1 & 1 & 3\\0 & 0 & -7 & -12\\0 & 0 & 0 & - \frac{4}{7}\end{matrix}\right] \Rightarrow \det(A)= \left|\begin{matrix}1 & 0 & -2 & -1\\0 & 1 & 1 & 3\\0 & 0 & -7 & -12\\0 & 0 & 0 & - \frac{4}{7}\end{matrix}\right| \\\quad = 1\cdot 1\cdot (-7) \cdot (-{4\over 7})= \bbox[red, 2pt] 4 \\\mathbf{(c)}\; [A\mid I]= \left[ \begin{array}{rrrr|rrrr}1 & 0 & -2 & -1 & 1 & 0 & 0 & 0\\2 & 1 & -3 & 1 & 0 & 1 & 0 & 0\\-2 & 4 & 1 & 2 & 0 & 0 & 1 & 0\\0 & 2 & 0 & 2 & 0 & 0 & 0 & 1\end{array} \right] \xrightarrow{R_2-2R_1\to R_2, R_3+2R_1\to R_3} \\\left[ \begin{array}{rrrr|rrrr}1 & 0 & -2 & -1 & 1 & 0 & 0 & 0\\0 & 1 & 1 & 3 & -2 & 1 & 0 & 0\\0 & 4 & -3 & 0 & 2 & 0 & 1 & 0\\0 & 2 & 0 & 2 & 0 & 0 & 0 & 1\end{array} \right] \xrightarrow{R_3-4R_2\to R_3, R_4-2R_2\to R_4} \left[ \begin{array}{rrrr|rrrr} 1 & 0 & -2 & -1 & 1 & 0 & 0 & 0\\0 & 1 & 1 & 3 & -2 & 1 & 0 & 0\\0 & 0 & -7 & -12 & 10 & -4 & 1 & 0\\0 & 0 & -2 & -4 & 4 & -2 & 0 & 1 \end{array} \right] \\ \xrightarrow{-(1/7)R_3 \to R_3} \left[ \begin{array}{rrrr|rrrr}1 & 0 & -2 & -1 & 1 & 0 & 0 & 0\\0 & 1 & 1 & 3 & -2 & 1 & 0 & 0\\0 & 0 & 1 & \frac{12}{7} & - \frac{10}{7} & \frac{4}{7} & - \frac{1}{7} & 0\\0 & 0 & -2 & -4 & 4 & -2 & 0 & 1 \end{array} \right] \xrightarrow{R_1+2R_3\to R_1, R_2-R_3\to R_2, R_4+2R_3\to R_4} \\\left[ \begin{array}{rrrr|rrrr}1 & 0 & 0 & \frac{17}{7} & - \frac{13}{7} & \frac{8}{7} & - \frac{2}{7} & 0\\0 & 1 & 0 & \frac{9}{7} & - \frac{4}{7} & \frac{3}{7} & \frac{1}{7} & 0\\0 & 0 & 1 & \frac{12}{7} & - \frac{10}{7} & \frac{4}{7} & - \frac{1}{7} & 0\\0 & 0 & 0 & - \frac{4}{7} & \frac{8}{7} & - \frac{6}{7} & - \frac{2}{7} & 1\end{array} \right] \xrightarrow{-(7/4)R_4\to R_4} \left[ \begin{array}{rrrr|rrrr}1 & 0 & 0 & \frac{17}{7} & - \frac{13}{7} & \frac{8}{7} & - \frac{2}{7} & 0\\0 & 1 & 0 & \frac{9}{7} & - \frac{4}{7} & \frac{3}{7} & \frac{1}{7} & 0\\0 & 0 & 1 & \frac{12}{7} & - \frac{10}{7} & \frac{4}{7} & - \frac{1}{7} & 0\\0 & 0 & 0 & 1 & -2 & \frac{3}{2} & \frac{1}{2} & - \frac{7}{4}\end{array} \right] \\ \xrightarrow{R_1-(17/7)R_4\to R_1, R_2-(9/7)R_4\to R_2, R_3-(12/7)R_4 \to R_3} \left[ \begin{array}{rrrr|rrrr}1 & 0 & 0 & 0 & 3 & - \frac{5}{2} & - \frac{3}{2} & \frac{17}{4}\\0 & 1 & 0 & 0 & 2 & - \frac{3}{2} & - \frac{1}{2} & \frac{9}{4}\\0 & 0 & 1 & 0 & 2 & -2 & -1 & 3\\0 & 0 & 0 & 1 & -2 & \frac{3}{2} & \frac{1}{2} & - \frac{7}{4}\end{array} \right] \\ \Rightarrow A^{-1}=\bbox[red, 2pt]{ \left[ \begin{array}{rrrr } 3 & - \frac{5}{2} & - \frac{3}{2} & \frac{17}{4}\\ 2 & - \frac{3}{2} & - \frac{1}{2} & \frac{9}{4}\\ 2 & -2 & -1 & 3\\ -2 & \frac{3}{2} & \frac{1}{2} & - \frac{7}{4}\end{array} \right]}$$

解答: $$u(x,t)=X(x)T(t) \Rightarrow XT''=X''T \Rightarrow {T''\over T}={X''\over X}=\lambda\\ \lambda\ge 0 \Rightarrow X=0 \Rightarrow u=0\\ \lambda\lt 0 \Rightarrow \lambda=-\rho^2 \Rightarrow X''+\rho^2=0 \Rightarrow X=c_1\cos \rho x+c_2 \sin \rho x \Rightarrow \cases{X(0)=c_1=0\\ X(L=\pi)= c_2\sin \rho \pi=0} \\ \Rightarrow \rho =1,2,\cdots \Rightarrow X_n=\sin n x\\ T''+\rho^2 T=0 \Rightarrow T=c_1\cos \rho t+c_2\sin \rho t \Rightarrow T_n=c_1\cos nt+c_2\sin nt \\ \Rightarrow u(x,t)=\sum_{n=1}^\infty (A_n \cos nt+B_n \sin nt)\sin(nx) \\ \Rightarrow u_t(x,t)=\sum_{n=1}^\infty (-nA_n \sin nt+ nB_n \cos nt)\sin(nx) \\ \Rightarrow u_t(x,0) =\sum_{n=1}^\infty nB_n\sin(nx)\\ \Rightarrow B_n={2\over n\pi} \int_0^\pi g(x) \sin(nx)\,dx ={2\over n\pi} \left( \int_0^{\pi/2} 0.01x\sin(nx)\,dx + \int_{\pi/2}^\pi 0.01(\pi-x)\sin(nx)\,dx\right) \\={0.02\over n\pi} \left(\left. \left[{\sin(nx)-nx\cos(nx)\over n^2}  \right] \right|_0^{\pi/2} + \left. \left[ -{\sin(nx)+n(\pi-x)\cos(nx) \over n^2}\right] \right|_{\pi/2}^\pi \right) \\={0.02\over n\pi }\cdot {2\sin(n\pi/2) \over n^2} ={0.04\over n^3\pi} \sin(n\pi/2) \Rightarrow B_n={0.04\over n^3\pi} \sin(n\pi/2)\\ u(x,0)=0 \Rightarrow u(x,t)=\sum_{n=1}^\infty A_n   \sin(nx)=0 \Rightarrow A_n=0 \\ \Rightarrow \bbox[red, 2pt]{u(x,t)=\sum_{n=1}^\infty  {0.04\over n^3\pi} \sin(n\pi/2) \sin (nt) \sin(nx)}$$

解答: $$\textbf{(a)}\; \begin{vmatrix}\vec i & \vec j& \vec k\\ \frac{\partial }{\partial x}& \frac{\partial }{\partial y} & \frac{\partial }{\partial z}\\y^2\cos x+z^3 & 2y\sin x-4& 3xz^2+2 \end{vmatrix} =2y\cos x\vec k+3z^2 \vec j-2y\cos x\vec k-3z^2 \vec j=0 \\\qquad \Rightarrow \vec F\text{ is a conservative field}. \bbox[red, 2pt]{QED}\\ \textbf{(b)}\; \text{Let } \nabla\Phi= \mathbf F, \text{ then }\Phi_x= y^2\cos x+z^3 \Rightarrow \Phi =\int (y^2\cos x+z^3)\,dx \\ \Rightarrow \Phi=y^2\sin x+xz^3+ \phi(y,z) \Rightarrow \Phi_y=2y\sin x+\phi_y=2y\sin x-4\\ \Rightarrow \phi_y=-4 \Rightarrow \phi(y,z)=-4y +\rho(z) \Rightarrow \Phi = y^2\sin x+xz^3-4y+\rho(z) \\ \Rightarrow \Phi_z=3xz^2+\rho'(z)=3xz^2+2 \Rightarrow \rho'(z)=2 \Rightarrow \rho(z)=2z+c_1\\ \Rightarrow \bbox[red, 2pt]{\Phi = y^2\sin x+xz^3-4y+2z+ c_1}\\ \textbf{(c)}\; \Phi(\pi/2,-1,2)-\Phi(1,1,-1) =(1+4\pi +4+4) -(\sin 1-1-4-2)=\bbox[red, 2pt]{4\pi +2-\sin 1}$$

解答: $$\vec r(u,v)=[u,v,6u-9v] \Rightarrow \cases{\vec r_u=[1,0,6] \\ \vec r_v=[0,1,-9]} \Rightarrow \vec r_u\times \vec r_v =[-6,9,1]\\ \vec F(u,v)=[ 5u,v^3,0] \Rightarrow \int \vec F\cdot (\vec r_u\times \vec r_v )dudv = \int_{-1}^1 \int_0^2 -30u+9v^3\,dudv \\=\int_{-1}^1 -60+18v^3\,dv= \bbox[red, 2pt]{-120}$$

==================== END ======================

解題僅供參考,其他歷年試題及詳解