113年台科大材料碩士班-工程數學詳解

 國立臺灣科技大學113學年度碩士班招生試題

系所組別：材料科學與工程系碩士班乙組
科目：工程數學

解答：$$\textbf{(1)}\; \bbox[red, 2pt]{No}, \text{it is nonlinear. It cannot be written in the form of }a(x)y'+b(x)y=c(x) \\ \textbf{(2)}\; (y-4x)dx+(y-x)dy=0 \Rightarrow \cases{P(x,y)=y-4x\\ Q(x,y)=y-x} \Rightarrow \cases{P_y=1\\ Q_x=-1} \\ \quad \Rightarrow P_y\ne Q_x \Rightarrow \bbox[red, 2pt]{\text{Not Exact}} \\\textbf{(3)}\;\cases{ {P_y-Q_x\over Q} ={2\over y-x} \text{ is dependent on both of }x,y \\ \quad -{P_y-Q_x\over P} =-{2\over y-4x} \text{ is dependent on both of }x,y } \Rightarrow \bbox[red, 2pt]{No,} \\\qquad \text{the ODE have no integrating factor }I(x) \text{ or }I(y) \\ \textbf{(4)}\; xM+yN= -4x^2+y^2 \Rightarrow \mu(x,y)={1\over -4x^2+y^2}\\\qquad  \Rightarrow (\mu M)_y={-4x^2+8xy-y^2 \over (4x^2-y^2)^2} =(\mu N)_x \Rightarrow \text{ exact} \\ \Rightarrow \Phi(x,y)= \int {4x-y\over 4x^2-y^2}\,dx =\int {x-y\over 4x^2-y^2}\,dy \\ \Rightarrow \Phi= {1\over 4}\ln(2x-y)(2x+y)^3+ \phi(y) ={1\over 4} \ln(y-2x)(2x+y)^3 +\rho(x) \\ \Rightarrow \bbox[red, 2pt]{\ln(2x-y)+3\ln(2x+y)=c_1}$$

解答：$$\cases{y(0)=c_1=-2\\ y(2\pi)=c_1=-2} \Rightarrow y=-2\cos(2x)+ c_2\sin(2x) \\ \Rightarrow \text{There are }\bbox[red, 2pt]{\text{infinitely many}}\text{ solutions with different }c_2$$

解答：$$y=ve^x \Rightarrow y'=v'e^x+ ve^x \Rightarrow y''=v''e^x+ 2v'e^x + ve^x \\ \Rightarrow (x-1)(v''e^x+ 2v'e^x + ve^x)-x(v'e^x+ ve^x)+ve^x=0 \Rightarrow (x-1)v''+(x-2)v'=0 \\ \Rightarrow v''={2-x\over x-1}v' \Rightarrow v'={c_1(x-1)\over e^x} \Rightarrow v=-{c_1 x\over e^x}+c_2 \Rightarrow \bbox[red, 2pt]{y=-c_1x+c_2e^x}$$

解答：$$\textbf{(1)}\;f(t)=t(u(t)-u(t-2))+u(t-2) \Rightarrow \bbox[red, 2pt]{f(t)= tu(t)+(1-t)u(t-2)} \\ \textbf{(2)}\; L\{f(t)\} =\int_0^\infty f(t) e^{-st}\,dt  = \int_0^2 te^{-st}\,dt +\int_2^\infty e^{-st}\,dt \\\quad = \left.\left[ -{1\over s}te^{-st}-{1\over s^2}e^{-st}\right] \right|_0^2 + \left. \left[ -{1\over s}e^{-st} \right] \right|_2^\infty ={1\over s^2}-{2\over s}e^{-2s}-{1\over s^2}e^{-2s}+{1 \over s}e^{-2s} \\ \quad \Rightarrow \bbox[red, 2pt]{ L\{f(t)\} ={1\over s^2}-{1\over s}e^{-2s}-{1\over s^2}e^{-2s}} \\\textbf{(3)}\;L\{y'\}+ L\{y\}=L\{f(t)\}  \Rightarrow sY(s)-1+Y(s)= {1\over s^2}-{1\over s}e^{-2s}-{1\over s^2}e^{-2s} \\\quad \Rightarrow Y(s)={1\over (s+1)s^2}-{1\over s(s+1)}e^{-2s}-{1\over (s+1)s^2}e^{-2s}+ {1\over s+1}\\  \Rightarrow y(t)=L^{-1}\{ Y(s)\} =-1+t+e^{-t}-u(t-2)(1-e^{2-t})-u(t-2)(t-3+e^{2-t})+e^{-t} \\ \Rightarrow \bbox[red, 2pt]{y(t)=-1+t+2e^{-t}-u(t-2)\left( t-2\right)}$$

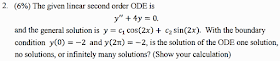
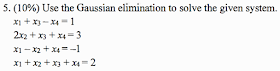
解答：$$\begin{cases}x_1 &    & +x_3 &-x_4  & = & 1 \\  & 2x_2  & + x_3 & +x_4  & = & 3 \\x_1 & -x_2 &   &+x_4  & = & -1\\ x_1& +x_2& +x_3& +x_4 &=& 2\end{cases} \Rightarrow \begin{bmatrix}1& 0  & 1&-1 \\0 & 2 & 1& 1\\ 1& -1 & 0 & 1\\ 1& 1& 1& 1 \end{bmatrix} \begin{bmatrix}x_1 \\x_2 \\x_3\\x_4\end{bmatrix}=\begin{bmatrix}1 \\3 \\-1\\2 \end{bmatrix} \\ \Rightarrow \text{augmented matrix} \left[ \begin{array}{rrrr|r}1 & 0 & 1 & -1 & 1 \\ 0 & 2 & 1 & 1 & 3 \\1 & -1 & 0 & 1 & -1 \\1 & 1 & 1 & 1 & 2\end{array} \right] \xrightarrow{R_3-R_1\to R_3,R_4-R_1\to R_4} \\ \left[ \begin{matrix} 1 & 0 & 1 & -1 & 1 \\0 & 2 & 1 & 1 & 3 \\0 & -1 & -1 & 2 & -2 \\0 & 1 & 0 & 2 & 1\end{matrix} \right] \xrightarrow{R_3+(1/2)R_2\to R_3, R_4-(1/2)R_2\to R_4} \left[ \begin{matrix}1 & 0 & 1 & -1 & 1 \\0 & 2 & 1 & 1 & 3 \\0 & 0 & \frac{-1}{2} & \frac{5}{2} & \frac{-1}{2} \\0 & 0 & \frac{-1}{2} & \frac{3}{2} & \frac{-1}{2} \end{matrix} \right] \\ \xrightarrow{R_4-R_3\to R_4} \left[ \begin{matrix}1 & 0 & 1 & -1 & 1 \\0 & 2 & 1 & 1 & 3 \\0 & 0 & \frac{-1}{2} & \frac{5}{2} & \frac{-1}{2} \\0 & 0 & 0 & -1 & 0 \end{matrix} \right] \Rightarrow \begin{cases} x_1 &  & +x_3 & -x_4 & = & 1 \\ &2x_2 & +x_3 & +x_4 & = & 3 \\ & &\frac{-1}{2}x_3 & +\frac{5}{2}x_4 & = & \frac{-1}{2} \\ & & &-x_4 & = & 0\end{cases} \\ \Rightarrow x_4=0 \Rightarrow -{1\over 2}x_3=-{1\over 2} \Rightarrow x_3=1 \Rightarrow 2x_2+1=3 \Rightarrow x_2=1 \Rightarrow x_1+1=1 \Rightarrow x_1=0 \\ \Rightarrow \bbox[red, 2pt]{\cases{x_1=0\\ x_2=1\\ x_3=1\\ x_4=0}}$$

解答：$$\begin{cases}x_1 & +2x_2 & +x_3 &  & = & 8 \\2x_1 & -2x_2 & +2x_3 &  & = & 7 \\x_1 & -4x_2 & +3x_3 &  & = & 1\end{cases} \Rightarrow \begin{bmatrix}1 & 2 & 1 \\2 & -2 & 2 \\1 & -4 & 3 \end{bmatrix} \begin{bmatrix}x_1 \\ x_2 \\x_3\end{bmatrix} =\begin{bmatrix}8 \\ 7 \\ 1\end{bmatrix} \\ \Rightarrow \cases{\triangle =\begin{vmatrix}1 & 2 & 1 \\2 & -2 & 2 \\1 & -4 & 3 \end{vmatrix} =-12 \\[1ex] \triangle_1= \left|\begin{matrix} 8 & 2 & 1 \\7 & -2 & 2 \\ 1 & -4 & 3 \end{matrix}\right| = -48\\[1ex] \triangle_2 =\left|\begin{matrix} 1 & 8 & 1 \\ 2 & 7 & 2 \\1 & 1 & 3\end{matrix}\right| = -18 \\[1ex] \triangle_3= \left|\begin{matrix} 1 & 2 & 8 \\2 & -2 & 7 \\1 & -4 & 1 \end{matrix}\right| =-12} \Rightarrow \cases{x_1=\triangle_1/\triangle =-48/-12=4 \\x_2= \triangle_2/\triangle = -18/-12= 3/2 \\ x_3=\triangle_3/ \triangle = -12/-12 =1}  \Rightarrow \bbox[red, 2pt]{ \cases{x_1= 4 \\x_2 = 3/2 \\ x_3  =1}}$$

解答：$$A=\begin{bmatrix}1 & 6 &0 \\0 & 2& 1\\ 0 & 1& 2 \end{bmatrix} \Rightarrow \det(A-\lambda I)= -(\lambda-1)^2(\lambda-3)\\ \lambda_1=1 \Rightarrow (A-\lambda_1 I)v=0 \Rightarrow \begin{bmatrix}0 & 6 & 0 \\0 & 1 & 1 \\0 & 1 & 1 \end{bmatrix} \begin{bmatrix}x_1 \\x_2\\ x_3 \end{bmatrix} =0 \Rightarrow x_2=x_3=0\\\qquad \Rightarrow v=x_1 \begin{pmatrix}1 \\0\\0 \end{pmatrix}, \text{ choose }v_1= \begin{pmatrix}1 \\0\\0 \end{pmatrix} \\ \lambda_2=3  \Rightarrow (A-\lambda_2 I)v=0 \Rightarrow \begin{bmatrix}-2 & 6 & 0 \\0 & -1 & 1 \\ 0 & 1 & -1 \end{bmatrix} \begin{bmatrix}x_1 \\x_2\\ x_3 \end{bmatrix} =0 \Rightarrow \cases{x_1=3x_3\\ x_2=x_3} \\\qquad \Rightarrow v=x_3 \begin{pmatrix}3 \\1\\ 1 \end{pmatrix}, \text{ choose }v_2= \begin{pmatrix}3 \\1\\ 1 \end{pmatrix}\\ \Rightarrow \text{eigenvalues: }\bbox[red, 2pt]{1,3}, \text{ eigenvectors: } \bbox[red, 2pt]{\begin{pmatrix}1 \\0\\0 \end{pmatrix} ,\begin{pmatrix}3 \\1\\ 1 \end{pmatrix}}$$

解答：$$$$