114年國中教育會考-數學詳解

 114年國中教育會考數學科試題本

第一部分：選擇題 (1 ～ 25 題)

解答:$$7^{10}\times 7^2 \div 7^4 =7^{10+2-4} =7^{8}，故選\bbox[red, 2pt]{(C)}$$

解答:$$(5x^2-2x)-(4-3x) =5x^2-2x-4+3x =5x^2+x-4，故選\bbox[red, 2pt]{(B)}$$

解答:

$$(A)對稱軸為斜線\\ (B)對稱軸為垂直線\\ (D)對稱軸為水平線，故選\bbox[red, 2pt]{(C)}$$

解答:$$\cases{37x+2y=81 \cdots(1)\\ 23x-2y=39 \cdots(2)} \Rightarrow 兩式相加可得60x=120 \Rightarrow x=2代回第(1)式\Rightarrow 74+2y=81 \\ \Rightarrow y={7\over 2} \Rightarrow \cases{a=2\\ b=7/2} \Rightarrow a+2b=2+7=9，故選\bbox[red, 2pt]{(B)}$$

解答:$$\triangle ACD中，r^\circ=180^\circ-30^\circ-70^\circ =80^\circ  \\\triangle ABD中，r^\circ=p^\circ+q^\circ \Rightarrow p+q+r=2r=2\times 80=160，故選\bbox[red, 2pt]{(C)}$$

解答:

$$只有A在P的下方及右方，故選\bbox[red, 2pt]{(A)}$$

解答:$$\cases{60-70歲減少109人\\ 70-80歲增加112人\\ 80至90歲以上增加204人} \Rightarrow 合計(-109)+112+204=207，故選\bbox[red, 2pt]{(A)}$$

解答:$$(2\sqrt 3+\sqrt 6) \times \sqrt 2 = 2\sqrt 6+\sqrt{12} =2\sqrt 6+2\sqrt 3，故選\bbox[red, 2pt]{(C)}$$

解答:$$停車位有20個，下車區有19個，因此總寬度為200\times 20+150\times 19=6850，故選\bbox[red, 2pt]{(A)}$$

解答:$$(A)(106^2-4^2)\times (108^2-2^2) =(106+4)(106-4)\times(108+2)(108-2) =110\times 102 \times 110\times 106 \\(B)(107^2-3^2) \times (107^2-1^2) =110\times 104\times 108\times 106\\ (C)(108^2-2^2) \times (106^2-2^2)=110\times 106\times 108\times 104 \\(D)(109^2-1^2)\times (105^2-1^2)=110\times 108\times 106\times 104\\ 只有(A)與其他不同，故選\bbox[red, 2pt]{(A)}$$

解答:$$\cases{阿嘉蓋住的牌為:2,4,5\\ 小楊蓋住的牌為:1,3,4} \Rightarrow 阿嘉比小楊大的情形:(2,1),(4,1),(4,3),(5,1),(5,3),(5,4)，共六種\\ 全部的情況有3\times 3=9，因此機率={6\over 9}={2\over 3}，故選\bbox[red, 2pt]{(B)}$$

解答:$$正三角錐的斜邊長需相等，乙的邊長一邊為3另一邊2不能成為正三角錐；\\而丙的兩邊皆為4，可以組成正三角錐，故選\bbox[red, 2pt]{(D)}$$

解答:$$甲:(x-4)^2=9 \Rightarrow \cases{x-4=3\\ x-4=-3} \Rightarrow \cases{x=7\\ x=1} 有兩相異解\\ 乙:(x+9)^2=-4, 由於(x+9)^2\ge 0，因此無解\\，故選\bbox[red, 2pt]{(A)}$$

解答:$$假設售出早餐組合x組，也就是x杯咖啡及x個三明治，剩下120-x杯咖啡及剩下100-x個三明治\\由於全部售出，因此收入為70x+ (120-x)50+(100-x)40 =8700\\ \Rightarrow -20x+10000=8700 \Rightarrow 20x=1300 \Rightarrow x=65 \Rightarrow 早餐數入65\times 70=4550，故選\bbox[red, 2pt]{(C)}$$

解答:$$假設 \overline{AB}= \overline{BC}= \overline{CD}= \overline{DE}= k\\ 若C為原點, 則\cases{|a|+|b|=2k+k=3k\\ |e|=2k} \Rightarrow 原點在C的左邊\\ 若B為原點, 則\cases{|a|+|b|=a+0=a\\ |e|=3k} \Rightarrow 原點在B的右邊\\ 若原點在\overline{BC}的中間, 則\cases{|a|+|b|=k+k/2+k/2=2k\\ |e|=2.5k} \Rightarrow 原點在\overline{BC}中點的右邊\\ 由以上可知:原點在\overline{BC}上且較接近C點，故選\bbox[red, 2pt]{(B)}$$

解答:$$\overline{EF} // \overline{BC} \Rightarrow {\overline{AE} \over \overline{EB}}={\overline{AF} \over \overline{FC}} ={7\over 3} \Rightarrow \overline{EB}={3\over 10} \overline{AB}\\ D為\overline{AB}中點\Rightarrow \overline{DB}={1\over 2}\overline{AB} \Rightarrow \overline{DE}=\overline{DB}-\overline{EB}={1\over 2}\overline{AB}-{3\over 10}\overline{AB}={2\over 10}\overline{AB} \Rightarrow \overline{DE} \lt \overline{EB} \\ 又{\overline{AD} \over \overline{DE}} ={{1\over 2}\overline{AB} \over {2\over 10}\overline{AB}} ={5\over 2}\ne {7\over 3}={\overline{AF} \over \overline{FC}} \Rightarrow \overline{DF}與\overline{EC}不平行，故選\bbox[red, 2pt]{(D)}$$

解答:$$正三角形特性可知:假設螺紋間距為a \Rightarrow H={\sqrt 3\over 2}a \Rightarrow 螺紋深度=H-{H\over 8}-{H\over 4}={5\over 8}H\\={5\over 8}\times {\sqrt 3\over 2}a={5\sqrt 3\over 16}a，故選\bbox[red, 2pt]{(D)}$$

解答:$$增加一個數，最大公因數會變小，最小公倍數會變大，因此兩人都錯，故選\bbox[red, 2pt]{(B)}$$

解答:$$16人電影票花費320\times 16=5120，剩下6000-5120=880元，需買16杯飲料\\假設\cases{使用優惠一a次\\ 使用優惠二b次 }，需滿足條件 \cases{a+b=16\\ 35a+90b\le 880}\\ a=16-b \Rightarrow 35(16-b)+90b=560+55b\le 880 \Rightarrow 55b\le 320 \Rightarrow b=5，故選\bbox[red, 2pt]{(C)}$$

解答:

$$\overline{BE}為摺線 \Rightarrow \cases{\angle PBE= \angle ABE =\angle 1\\ \angle PEB =\angle AEB=\angle 6}, \quad\overline{BF}為摺線\Rightarrow \cases{\angle PBF=\angle CBF=\angle 2\\ \angle PFB= \angle BFC=\angle 3} \\ \overline{EF}為摺線\Rightarrow \cases{\angle PEF=\angle DEF=\angle 5\\ \angle PFE=\angle EFD=\angle 4}\\ C,F,D在一直線上\Rightarrow \angle 3+\angle 3+\angle 4+ \angle 4=180^\circ \Rightarrow \angle 3+\angle 4=90^\circ \\ 又\triangle BFE中，\overline{BE}\gt \overline{FE}\gt \overline{BF} \Rightarrow  \angle 3+\angle 4\gt \angle 1+\angle 2\gt \angle 5+\angle 6\\，故選\bbox[red, 2pt]{(A)}$$

解答:

$$y=f(x)=-(x+7)^2+12 \xrightarrow {向右平移10點} y=f(x-10) =-(x-3)^2+12\\平移前頂點坐標(-7,12), y截距為-49+12=-37, \\再向右移7點，頂點在y軸上，此時y截距為12\\ 再向右多3點，頂點為(3,12)，y截距為-9+12=3 \\ 因此y截距向上再向下，故選\bbox[red, 2pt]{(D)}$$

解答:

$$G為重心\Rightarrow \triangle ABP={1\over 2}\triangle ABC\\ G為重心\Rightarrow {\overline{AG} \over \overline{GP}}={2\over 1} \Rightarrow \triangle ABG ={2\over 3}\triangle ABP ={2\over 3}\cdot {1\over 2}\triangle ABC ={1\over 3 }\triangle ABC \\ {\overline{AE} \over \overline{EB}} ={3\over 4} \Rightarrow \triangle AEG={3\over 7} \triangle ABG={3\over 7}\cdot {1\over 3}\triangle ABC ={1\over 7}\triangle ABC \\  {\overline{DE} \over \overline{EG}} ={3\over 2} \Rightarrow \triangle AEG ={2\over 5} \triangle ADG \Rightarrow \triangle ADG={5\over 2}\triangle AEG= {5\over 2}\cdot {1\over 7} \triangle ABC={5\over 14} \triangle ABC\\，故選\bbox[red, 2pt]{(B)}$$

解答:

$$\cases{\stackrel{\Large\frown}{BC} =54^\circ \Rightarrow \angle BAC=27^\circ\\ \stackrel{\Large\frown}{CA} =62^\circ \Rightarrow \angle ABC=31^\circ} \Rightarrow \angle ACB=180^\circ-27^\circ-31^\circ=122^\circ \\ \triangle ABC與\triangle AB'C'全等 \Rightarrow \cases{\angle C'AB'= \angle CAB=27^\circ\\ \angle AB'C'= \angle ABC=31^\circ\\ \angle AC'B'=\angle ACB=122^\circ} \\  由於 \cases{\angle C'B'A=31^\circ \\ \stackrel{\Large\frown}{AC} =62^\circ} \Rightarrow B'C'C在一直線上 \Rightarrow \angle AB'B=(62^\circ+54^\circ)/2=58^\circ \\ 又\overline{AB} =\overline{AB'} \Rightarrow \angle ABB'=\angle AB'B=58^\circ \\ 對同弧的\angle ACB'=\angle ABB'=58^\circ\Rightarrow \angle AC'B'=\angle CAC'+ \angle ACC' \Rightarrow 122^\circ= x+27^\circ+58^\circ \\ \Rightarrow x=37^\circ ，故選\bbox[red, 2pt]{(D)}$$

解答:$$原齒輪比 r={33\over 21} \\ \cases{\cases{(A) 齒輪比a={33\over 18} \\(B)齒輪比b={33\over 24}} \Rightarrow a\gt b \\ \cases{(C)齒輪比c={22\over 21} \\(D)齒輪比d={44\over 21}} \Rightarrow d\gt c}  \Rightarrow \cases{a=33/18=11/6 =77/42 \\d=44/21=88/42} \Rightarrow d\gt a，故選\bbox[red, 2pt]{(D)}$$

解答:$$(A){11\over 6}={33\over 18} ={44\over 24} \Rightarrow 2種組合\\ (B){11\over 7}={22\over 14} ={33\over 21} ={44\over 28} \Rightarrow 3種組合\\  (C){11\over 8}={22\over 16} ={33\over 24}  \Rightarrow 2種組合 \\(D) {11\over 9}={22\over 18} \Rightarrow 1種組合，故選\bbox[red, 2pt]{(B)}$$

解答:$$\textbf{(1)}調整倍率={該組人口占比\\ 該組調查比率} ={20\%\over 40\%} =\bbox[red, 2pt]{0.5} \\\textbf{(2) } \begin{array} {} 組別& 人口占比& 調查比率& 調整比率& 調整前&&調整後 \\\hline 18-39& 40\%&  20\% & 2 & 8\%& 12\% &16\% & 24\%\\\hline 40-59& 40\%   & 40\% & {\color{blue}1} & x\% & y\% & x\% & y\% \\\hline 60歲以上& 20\%& 40\% & {\color{blue}0.5}& a\% &b\% & 0.5a\%& 0.5b\%\\\hline 總計& 100\% & 100\% &&56\%& 44\%& 49\%& 51\% \\\hline\end{array} \\ \Rightarrow \cases{8+x+a=56 \\ 12+y+b=44\\16+x+0.5a=49 \\ 24+y+05b=51} \Rightarrow \cases{x=18\\y=22\\ a=30 \\b=10} \Rightarrow \bbox[red, 2pt]{\cases{40-59歲組調整前贙成比率18\%\\ 60歲以上組調整前贙成比率30\%}}$$

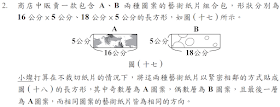
解答:$$\textbf{(1)}16,18的最最小公倍數為144，也就是A圖案至少144/16=\bbox[red, 2pt]9個 \\\textbf{(b)} 每一層\cases{A圖案9張\\ B圖案8張},又假設B圖案有n層、A圖案有n+1層 ,共需 \cases{A圖案9(n+1) 張\\ B圖案8n張} \\\quad 因此{9(n+1)\over 8n}={4\over 3} \Rightarrow 5n=27 \Rightarrow n不是整數，\bbox[red, 2pt]{無法剛好用完}$$

====================== END ==========================
解題僅供參考，其他國中會考試題及詳解