114年內湖高中教甄-數學詳解

 臺北市立內湖高級中學114 學年度第 1 次正式教師甄選

本試題共 20 題填充題，每題 5 分，共 100 分。

解答:$$利用長除法: x^{10} =(x+1)^3(x^7-3x^6+6x^5-10x^4+15x^3-21x^2+28x-36) +45x^2+80x+36 \\ \Rightarrow R(x)= 45x^2+80x+36 \Rightarrow R(1)= \bbox[red, 2pt]{161}$$

解答:$$\log x^{\log x}+ \log x^3-5=0 \Rightarrow(\log x)^2+3\log x-5=0 \Rightarrow 兩根之和=\log \alpha+\log \beta=-3 \\ \Rightarrow \log (\alpha \beta)=-3 \Rightarrow \alpha \beta=10^{-3} = \bbox[red, 2pt]{1\over 1000}$$

解答:

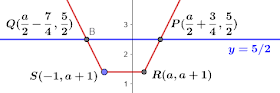
$$y=f(x)=|x-a|+|x+1| \Rightarrow \begin{cases}L_1: y=2x-a+1 & x\ge a\\ L_2:y=a+1 & -1\le x\le a\\ L_3: y=-2x+a-1& x\le -1\end{cases} \\ \Rightarrow \cases{P=L_1\cap  (y=5/2) =(a/2+3/4,5/2)\\ Q=L_3\cap (y=5/2) =(a/2-7/4, 5/2) \\ R=L_1\cap L_2 =(a,a+1) \\S=L_3\cap L_2 =(-1,a+1)} \Rightarrow \cases{\overline{PQ} =5/2 \\ \overline{RS}=a+1\\ d(L_2, y=a+1)=3/2-a} \\ \Rightarrow 梯形PQSR  =({5\over 2}+a+1)({3\over 2}-a)/2=2 \Rightarrow ({7\over 2}+a)({3\over 2}-a)=4 \Rightarrow a^2+2a-{5\over 4}=0 \\ \Rightarrow a=\bbox[red, 2pt]{1\over 2}$$

解答:$$f(x)=|3 \sin x+4\cos x|=| 5\sin(x+\alpha)|,其中\cos x={3\over 5}, \sin x={4\over 5} \\ \Rightarrow 當x+\alpha={3\pi\over 2}時,f(x)有最大值 \Rightarrow k={3\pi\over 2}-\alpha \Rightarrow \sin k-\cos k =\sin({3\pi\over 2}-\alpha)-\cos({3\pi\over 2}-\alpha) \\=-\cos \alpha+\sin \alpha=-{3\over 5}+ {4\over 5} = \bbox[red, 2pt]{1\over 5}$$

解答:$$假設三角形三邊長為a,b,c及其對應的高為{1\over 2},{1\over 3},{1\over 4} \Rightarrow {a\over 2}={b\over 3}={c\over 4} \\ \Rightarrow a:b:c=2:3:4 \Rightarrow \cases{a=2t\\ b=3t\\ c=4t} \Rightarrow s=(a+b+c)/2=9t/2 \\ \Rightarrow a\triangle ABC=\sqrt{s(s-a) (s-b)(s-c)}= \sqrt{{9t\over 2}\cdot {5t\over 2} \cdot {3t\over 2}\cdot {t\over 2}} ={3\sqrt{15}t^2\over 4} ={1\over 2}\cdot 2t\cdot {1\over 2} ={t\over 2} \\ \Rightarrow t={2\over 3\sqrt{15}} \Rightarrow 周長=2s=9t ={6\over \sqrt{15}} = \bbox[red, 2pt]{2\sqrt{15}\over 5}$$

解答:$$f(x)=2ax^3-3ax^2+b \Rightarrow f'(x)=6ax^2-6ax = 6ax(x-1) =0 \Rightarrow 當x=0,1時, f(x)有極值\\ \Rightarrow f''(x)= 12ax-6a=6a(2x-1) \\ \textbf{Case I }a\gt 0: f(x)\begin{cases}遞增 & x\ge 1\\ 遞減& 0\le x\le 1\\ 遞增& x\le 0 \end{cases} \Rightarrow \cases{f(2)=4a+b\\ f(0)=b} \Rightarrow f(2)\gt f(0) \\\qquad \Rightarrow \cases{f(2)=4a+b=7\\ f(1)=-a+b=-3} \Rightarrow \cases{a=2\\ b=-1} \\\textbf{Case II }a\lt 0: f(x)\begin{cases}遞減 & x\ge 1\\ 遞增& 0\le x\le 1\\ 遞減& x\le 0 \end{cases} \Rightarrow \cases{ f(0)=b\\ f(2)=4a+b} \Rightarrow f(0)\gt f(2) \\\qquad \Rightarrow \cases{f(1)=-a+b=7\\ f(2) = 4a+b=-3} \Rightarrow \cases{a=-2\\ b=5} \\ \Rightarrow (a,b)=\bbox[red, 2pt]{(2,-1)或 (-2,5)}$$

解答:$$\cases{A(0,0,0) \\ B(a,0,a)\\ C(0,a,a)\\ D(a,a,0)} \Rightarrow 稜長=\sqrt 2 a=1 \Rightarrow a=1/\sqrt 2 \Rightarrow \cases{E=(A+B)/2=(a/2,0,a/2) \\F=(C+D)/2 =(a/2,a,a/2)} \\ \Rightarrow G=(A+E+F)/3 =(a/3, a/3,a/3) \Rightarrow \overline{BG}=a= \bbox[red, 2pt]{\sqrt{2}\over 2}$$

解答:$$代公式{2\over 3}R^3 \tan \theta ={2\over 3}\cdot 3^3 \tan 45^\circ = \bbox[red, 2pt]{18}\\ \href{https://chu246.blogspot.com/2020/12/blog-post.html}{公式證明}$$

解答:$$\cases{\overleftrightarrow{AB} \parallel \overleftrightarrow{CD} \\\overleftrightarrow{AB}通過(6,0)\\ \overleftrightarrow{CD}通過(0,8)}\Rightarrow \cases{\overleftrightarrow{AB}: y=m(x-6) \\ \overleftrightarrow{CD} :y=mx+8}, 同理\cases{\overleftrightarrow{BC}: y=-{1\over m}(x-6)+6\\ \overleftrightarrow{AD}: y=-{1\over m}(x+5)+4} \\ d(\overleftrightarrow{AB}, \overleftrightarrow{CD}) = d(\overleftrightarrow{BC}, \overleftrightarrow{AD}) \Rightarrow {|8+6m| \over \sqrt{m^2+1}} ={|2m+ 11| \over \sqrt{m^2+1}} \Rightarrow (8+6m)^2=(2m+11)^2 \\ \Rightarrow 32m^2+52m-57=0 \Rightarrow (4m-3)(8m+19)=0 \\ \Rightarrow \cases{m=3/4 \Rightarrow  d(\overleftrightarrow{AB},\overleftrightarrow{CD}) =10 \\ m=-19/8 \Rightarrow E\not \in \overline{AB}} \Rightarrow 面積=10^2= \bbox[red, 2pt]{100}$$

解答:$$矩陣A有n個0,{n^2-n\over 2}個2及{n^2-n\over 2}個-1 \Rightarrow \cases{P(X=0)=1/n\\ P(X=2) =1/2-1/(2n)\\ P(X=-1) =1/2-1/(2n)} \\ \Rightarrow \cases{EX=2(1/2-1/(2n))-(1/2-1/(2n)) = 1/2-1/(2n) \\ EX^2= 2^2(1/2-1/(2n))+(-1)^2(1/2-1/(2n)) = 5/2-5/(2n)} \\ \Rightarrow Var(X)=EX^2-(EX)^2={5\over 2}-{5\over 2n}-\left({1\over 2}-{1\over 2n} \right)^2 ={9\over 4}-{2\over n}-{1\over 4n^2}=1.84\\ \Rightarrow 1.64n^2-8n-1=0 \Rightarrow (n-5)(1.64n+0.2)=0 \Rightarrow n= \bbox[red, 2pt]5$$

解答:$$\cases{\sum x_i=400\\ \sum y_i=900} \Rightarrow \cases{EX=400/20=20\\ EY=900/20=45} \Rightarrow \cases{E(X')=E(2X-4)=2\cdot 20-4=36\\ E(Y') =E(-3Y+5) =-3\cdot 45+5=-130} \\(x_i,y_i)迴歸直線經過(x_1,y_1)=(30,40)及(EX,EY)=(20,45) \Rightarrow y=-{1\over 2}x+55 \Rightarrow \cases{a=-1/2\\ b=55} \\ \Rightarrow a=-{1\over 2} ={Cov(X,Y)\over Var(X)}\\ (x_i',y_i')迴歸直線斜率m= {Cov(X',Y')\over Var(X')} ={Cov(2X-4,-3Y+5) \over Var(2X-4)} ={-6Cov(X,Y) \over4Var(X)}\\ =-{6\over 4}\cdot (-{1\over 2}) ={3\over 4 } \Rightarrow y={3\over 4}(x-36)-130 \Rightarrow \bbox[red, 2pt]{y={3\over 4}x-157}$$

解答:$${x^2 \over 100} +{y^2\over 75}=1 \Rightarrow \cases{a=10\\ b=5\sqrt 3} \Rightarrow c=5 \Rightarrow 焦點\cases{F_1(-5,0) \\F_2(5,0)} \\ \overline{PQ}斜率=\tan 60^\circ =\sqrt 3 \Rightarrow L=\overleftrightarrow{PQ}:y=\sqrt3 (x-5) \Rightarrow {x^2\over 100}+{3(x-5)^2\over 75} =1\\ \Rightarrow 5x^2-40x=5x(x-8)=0 \Rightarrow \cases{x=0 \Rightarrow y=5\sqrt 3\\ x=8 \Rightarrow y=3 \sqrt 3} \Rightarrow \cases{P(0,5\sqrt 3) \\ Q(8, 3\sqrt 3)} \\ \Rightarrow \triangle OPQ ={1\over 2} \begin{Vmatrix}0& 5\sqrt 3& 1\\ 8&3\sqrt 3& 1\\ 0& 0& 1 \end{Vmatrix} = \bbox[red, 2pt]{20\sqrt 3}$$

解答:

$$假設梯形ABCD的高為h=\overline{CE} =\overline{DF}及\overline{AF}=a \Rightarrow \overline{BE}=5-a \\ \Rightarrow h^2=\overline{AD}^2-\overline{AF}^2=\overline{BC}^2-\overline{BE}^2 \Rightarrow 20-a^2=25-(5-a)^2 \Rightarrow a=2 \Rightarrow h=4\\ 又\triangle PBN \sim \triangle CBE (AAA) \Rightarrow \overline{PN}:\overline{BN}: \overline{PB} =\overline{CE}: \overline{BE}:\overline{BC}=4:3:5 \Rightarrow \cases{\overline{PN}=4k\\ \overline{BN}=3k\\ \overline{PB}=5k}\\ 同理\triangle AMP \sim \triangle AFD \Rightarrow \overline{AM}: \overline{MP}:\overline{AP} =\overline{AF}: \overline{FD}: \overline{AD} \Rightarrow \overline{AM}: \overline{MP}:10-5k = 2:4:2\sqrt 5 \\ \Rightarrow \cases{\overline{AM} =(2-k)\sqrt 5 \\ \overline{MP} =(4-2k)\sqrt 5} \\ \Rightarrow a\triangle APM+ a\triangle BPN= {1\over 2} \overline{AM}\cdot \overline{MP} +{1\over 2}\overline{BN}\cdot \overline{PN} ={1\over 2}(5(k-2)(2k-4) +12k^2) \\=f(k)=11k^2-20k+20 \Rightarrow 最小值=f(10/11)= \bbox[red,2pt]{120\over 11}$$

解答:$$\cases{P\in L_1\\ Q\in L_2} \Rightarrow \cases{P(s+3,-2s-1,2s) \\Q(-t+6,kt-1,-2t+6)} \\\textbf{Case I }k=1: P=Q \Rightarrow \cases{s+3=-t+6\\ -2s-1=t-1\\ 2s=-2t+6} \Rightarrow \cases{s=-3\\ t=6} \Rightarrow \cases{L_1\cap L_2=(0,5,-6) \\L_1\ne L_2} \\\textbf{Case II }k=2: P=Q \Rightarrow \cases{s+3=-t+6\\ -2s-1=2t-1\\ 2s=-2t+6} \Rightarrow 無解 L_1\cap L_2=\varnothing \\ \textbf{Case III }k=3:  P=Q\Rightarrow \cases{s+3=-t+6\\ -2s-1=3t-1\\ 2s=-2t+6} \Rightarrow \cases{s=9\\ t=-6} \Rightarrow \cases{L_1\cap L_2=(12,-19,18) \\L_1\ne L_2} \\\textbf{Case IV }k=4:P=Q \Rightarrow \cases{s+3=-t+6\\ -2s-1=4t-1\\ 2s=-2t+6} \Rightarrow \Rightarrow \cases{s=6\\ t=-3} \Rightarrow \cases{L_1\cap L_2=(9,-13,12) \\L_1\ne L_2} \\ \Rightarrow L_1與L_2相交機率= \bbox[red, 2pt]{3\over 4}$$

解答:$$a=b:(a,a,1,2), (a,a,2,1), (a,a,2,3), (a,a,3,2),(a,a,3,4), (a,a,4,3)\\\qquad (a,a,4,5),(a,a,5,4),(a,a,5,6), (a,a, 6,5),共10組, 又a=b=1-6 \Rightarrow 共60組\\ b=c:(a,b,b,b\pm 1):(a,1,1,2),(a,2,2,1),(a,2,2,3),(a,3,3,2), (a,3,3,4) \\\qquad (a,4,4,3),(a,4,4,5), (a,5,5,4),(a,5,5,6), (a,6,6,5),共10組,又a=1-6\Rightarrow 共60組\\ a=b=c:(1,1,1,2), (2,2,2,1), (2,2,2,3), (3,3,3,2), (3,3,3,4),( 4,4,4,3), (4,4,4, 5)\\ \qquad (5,5,5,4), (5,5,5,6),(6,6,6,5),共10組\\ c=d:(1,2,1,1),(3,2,1,1), (2,1,2,2),(2,3,2,2),(4,3,2,2) (1,2,3,3),(3,2,3,3)\\\qquad (3,4,3,3), (5,4,3,3),(2,3,4,4), (4,3,4,4), (3,5,4,4), (6,5,4,4), (3,4,5,5), (5,4,5,5)\\\qquad (5,6,5,5), (4,5,6,6),(6,5,6,6),共18組\\ 因此共有60+60-10+18=128組 \Rightarrow 機率={128\over 6^4}= \bbox[red, 2pt]{8\over 81}$$

解答:$$O(a,6,3)在E:2x+y-2z=8上 \Rightarrow 2a+6-6=8 \Rightarrow a=4 \Rightarrow O(4,6,3) \\ P\in L \Rightarrow P(t+4,2t+b,2t+c) 在E上\Rightarrow  2t+8+2t+b-4t-2c=8 \Rightarrow b=2c \\ \Rightarrow P(t+4,2t+2c,2t+c) \Rightarrow \overline{OP}=  \sqrt{t^2+(2t+2c-6)^2+(2t+c-3)^2} \\= \sqrt{9t^2+(12c-36)t+ 5c^2-30c+45} ,當t={6-2c\over 3}時有最小值6 \\ \Rightarrow (6-2c)^2-2(6-2c)^2 +5c^2-30c+45=6^2 \Rightarrow c^2-6c-27=0 \\ \Rightarrow (c-9)(c+3)=0 \Rightarrow \cases{c=9 \Rightarrow b=18\\ c=-3 \Rightarrow b=-6} \Rightarrow (a,b,c)= \bbox[red, 2pt]{(4,18,9)或,(4,-6,-3)}$$

解答:$$\begin{bmatrix}a_1 & a_2 & a_3 \\b_1 & b_2 & b_3 \\c_1 & c_2 &c_3 \end{bmatrix} \begin{bmatrix} a_1& b_1 & c_1 \\a_2 & b_2 & c_2 \\ a_3&  b_3 & c_3 \end{bmatrix} =\begin{bmatrix} 9& 0 &-6  \\0 & 25 &0  \\ -6& 0 & 16\end{bmatrix} \Rightarrow \cases{\vec a\cdot \vec a=9\\ \vec a\cdot \vec b=0 \\ \vec a\cdot \vec c=-6\\ \vec b\cdot \vec b=25\\ \vec b\cdot \vec c=0 \\ \vec c\cdot \vec c=16} \Rightarrow \cases{ |\vec a|=3\\ |\vec b|=5\\ |\vec c|=4\\ \vec a\bot \vec b \\ \vec b\bot \vec c}\\ 假設\vec a, \vec c夾角\theta \Rightarrow  \cos \theta ={\vec a\cdot \vec c\over |\vec a||\vec c|} ={-6\over 3\cdot 4} =-{1\over 2} \Rightarrow \theta =120^\circ \Rightarrow 所夾銳角為60^\circ \\ \Rightarrow \vec a,\vec  c 所夾之三角形面積={1\over 2}\cdot 3\cdot 4\cdot \sin 60^\circ =3\sqrt 3 \Rightarrow 四面體體積={1\over 3} \cdot |\vec b|\cdot 3\sqrt 3= \bbox[red, 2pt]{5\sqrt 3}$$

解答:$$\left( {n+3\over n}\right)+\left( {n+3\over n}\right)^2 + \cdots+\left( {n+3\over n}\right)^{2n} ={\left( \displaystyle {n+3\over n}\right)^{2n+1}-\left( \displaystyle {n+3\over n}\right) \over \left(\displaystyle  {n+3\over n}\right)-1} \\={\displaystyle {{n+3\over n}}\left( \displaystyle \left( {n+3\over n}\right)^{2n}-1\right) \over \displaystyle {  3\over n}}={n+3\over 3}\left( \displaystyle \left( {n+3\over n}\right)^{2n}-1\right) \\ \Rightarrow 原式=\lim_{n\to \infty}{n+3\over 3n} \left( \displaystyle \left( {n+3\over n}\right)^{2n}-1\right) = {1\over 3}\lim_{n\to \infty}\left(1+{3\over n} \right) \left( \displaystyle \left( 1+{3\over n}\right)^{(n/3)\cdot 6}-1\right) \\= \bbox[red, 2pt]{{1\over 3}(e^6-1)}$$

解答:$$\lfloor \sqrt k \rfloor =n \text{ if } k=n^2, n^2+1, \dots,(n+1)^2-1,共2n+1個\\ 又\sqrt{2025} =45 \Rightarrow -2+\sum_{k=1}^{2025}2^{\lfloor \sqrt k \rfloor} =-2+ \sum_{k=1}^{44} (2k+1)2^{k} +2^{45}= -2+ 2\sum_{k=1}^{44} k\cdot 2^{k}+ \sum_{k=1}^{44} 2^k+2^{45} \\= -2+2\cdot \left( 44\cdot 2^{46}-45 \cdot 2^{45} +2\right) +\left( 2^{45}-2\right) +2^{45} =(44\cdot 4-45\cdot 2+2) 2^{45} =88\cdot 2^{45} \\ \Rightarrow p=\bbox[red, 2pt]{88} \\ 註: \sum_{k=1}^n k\cdot 2^k=n\cdot 2^{n+2}-(n+1)2^{n+1}+2, \href{https://math.stackexchange.com/questions/30732/how-can-i-evaluate-sum-n-0-inftyn1xn?noredirect=1&lq=1}{公式來源}$$

解答:$$判別式\gt 0 \Rightarrow (k-2)^2-4(k^2+3k+5)\gt 0 \Rightarrow 3k^2+16k+16\lt 0 \Rightarrow (3k+4)(k+4)\lt 0 \\ \Rightarrow -4\lt k\lt -{4\over 3} \Rightarrow \cases{k=-3 \Rightarrow x^2-5x+5=0 \Rightarrow 無整數根\\k=-2 \Rightarrow x^2+4x+3=0 \Rightarrow x=-3-1} \Rightarrow k=\bbox[red, 2pt]{-2}$$

====================== END ==========================
解題僅供參考，其他教甄試題及詳解