關鍵字:國中、數學、基測
解:
$$將(3,b)代入3y=2x-9 \Rightarrow 3b=2\times 3-9 =-3 \Rightarrow b=-1,故選\bbox[red,2pt]{(A)}$$
$$7^3+(-4)^3=7^3-4^3 =(7-4)(7^2+7\cdot 4+4^2) =3(49+28+16) = 3\times 93=279,故選\bbox[red,2pt]{(C)}$$
$$將(3,b)代入3y=2x-9 \Rightarrow 3b=2\times 3-9 =-3 \Rightarrow b=-1,故選\bbox[red,2pt]{(A)}$$
(A)9 (B) 27 (C) 279 (D) 407
解:$$7^3+(-4)^3=7^3-4^3 =(7-4)(7^2+7\cdot 4+4^2) =3(49+28+16) = 3\times 93=279,故選\bbox[red,2pt]{(C)}$$
解:
$$5(2x-3)-4(3-2x) = 5(2x-3)+4(2x-3) = 9(2x-3) =18x-27,故選\bbox[red,2pt]{(D)}$$
$$5(2x-3)-4(3-2x) = 5(2x-3)+4(2x-3) = 9(2x-3) =18x-27,故選\bbox[red,2pt]{(D)}$$
解:
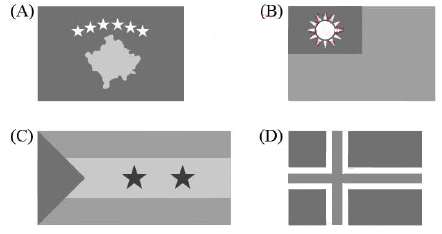
圖形為上下對稱,紅色為水平對稱線,故選(D)。
解:$$2x^2+5x-3 =(2x-1)(x+3) \Rightarrow 2x-1為其因式,故選\bbox[red,2pt]{(A)}$$
解:
累積次數一定是遞增圖形,所以(C)與(D)一定不對。
原次數分配圖前三項:34, 102, 136,累積次數為34, 136, 272。
累積次數第三項應為272, 圖(B)之第三項僅為170左右,故選(A)。
解:
$$令\angle B的外角=\angle A+\angle C= x,則\cases{2x=3\angle B \cdots(1)\\ x+\angle B=180^\circ \cdots(2)}\\由(2)可得\angle B=180^\circ-x代入(1) \Rightarrow 2x=3(180^\circ-x) = 540^\circ-3x \Rightarrow 5x=540^\circ \Rightarrow x=108^\circ\\,故選\bbox[red,2pt]{(C)}$$
解:$$(7x-a)^2 =49x^2-14ax +a^2 =49x^2-bx+9 \Rightarrow \cases{14a=b\\ a^2=9} \Rightarrow \cases{(a,b)=(3,42)\\ (a,b)= (-3,-42)}\\ \Rightarrow \cases{|a+b| =|3+42| =45\\ |a+b|=|-3-42|=45} \Rightarrow |a+b|=45,故選\bbox[red,2pt]{(D)}$$
解:$$\cases{5顆饅頭及3顆包子合計50+2元\\ 11顆饅頭及5顆包子打九折合計90元 } \\ \Rightarrow \cases{5x+3y=50+2\\ 0.9(11x+5y)=90 \Rightarrow 11x+5y= 90\div 0.9},故選\bbox[red,2pt]{(B)}$$
解:$$(a-1):7=4:5 \Rightarrow 5(a-1)= 7\times 4 \Rightarrow a-1={28\over 5} \Rightarrow a={28\over 5}+1={33\over 5}\\ \Rightarrow 10a+8 =10\times {33\over 5}+8=66+8=74,故選\bbox[red,2pt]{(C)}$$
解:$$16\lt 18\lt 25 \Rightarrow 4\lt \sqrt{18} \lt 5,再加上 4.5^2=20.25 ,因此4\lt \sqrt{18}\lt 4.5 ,故選\bbox[red,2pt]{(C)}$$
解:$${9^6\over 3^{12}} ={(3^2)^6\over 3^{12}} = {3^{12}\over 3^{12}} =1,故選\bbox[red,2pt]{(A)}$$
解:$$\mathbf{{1\over 2}+{2\over 3}+{3\over 4}\times (-4) ={1\over 2}+{2\over 3}-3={3\over 6}+{4\over 6}-{18\over 6} =-{11\over 6}},故選\bbox[red,2pt]{(B)}$$
解:$$\begin{array}{l|cc} 抓到糖果數 & 5 & 6 & 7 & 8 & 9 & 10& 11&12 &13 & 14& 15\\\hline 次數& 3 & 7 & 6 & 10 &11 & 8 & 13 & 7 & 1& 4 & 2\\\hline 累積次數 & 3 & 10 & 16 & 26 & 37 & 45 & 58 & 65 & 66 & 70& 72\\\hline \end{array} \\ 總人數為72,中位數為第36人與第37人抓到糖果的平均數\\,由上表累積次數可知第36人與第37人抓到的糖果數皆為9,即a=9;\\又抓到11個糖果的人數最多(13人),所以b=11;因此a+b=9+11=20,故選\bbox[red,2pt]{(A)}$$
解:
$$由摺線\overline{BD}可知:\angle ABD=\angle CBD\cdots(1) \\ 由B摺向D可知: \overline{CB}=\overline{CD} \Rightarrow \angle CBD= \angle BDC\cdots(2)\\ 由(1)及(2) 可知: \angle ABD =\angle BDC \Rightarrow \overline{AB}\parallel \overline{CD} (內錯角相等),故選\bbox[red,2pt]{(B)}$$
解:
解:$$(a-1):7=4:5 \Rightarrow 5(a-1)= 7\times 4 \Rightarrow a-1={28\over 5} \Rightarrow a={28\over 5}+1={33\over 5}\\ \Rightarrow 10a+8 =10\times {33\over 5}+8=66+8=74,故選\bbox[red,2pt]{(C)}$$
解:$${9^6\over 3^{12}} ={(3^2)^6\over 3^{12}} = {3^{12}\over 3^{12}} =1,故選\bbox[red,2pt]{(A)}$$
解:$$-{1\over 5}x-3 \gt 2 \Rightarrow -x-15\gt 10 \Rightarrow -x\gt 25 \Rightarrow x\lt -25,故選\bbox[red,2pt]{(A)}$$
解:$$\mathbf{{1\over 2}+{2\over 3}+{3\over 4}\times (-4) ={1\over 2}+{2\over 3}-3={3\over 6}+{4\over 6}-{18\over 6} =-{11\over 6}},故選\bbox[red,2pt]{(B)}$$
滾完一圈,C點座標由(1,0)→(6,0)
滾完n圈,C點座標由(1,0)→(1+5n,0)
滾完14圈,C點座標(71,0);滾完15圈,C點座標(76,0)
所以(75,0)的點為B,故選(B)。
解:$$\cases{A(-3)\\ B(-6)\\ \overline{AC}=4\\ \overline{BD}=1} \Rightarrow \cases{\cases{C(-7)\\ C(1)} \\\cases{D(-5)\\ D(-7)}} \Rightarrow \overline{CD}=\cases{\overline{-7,-5}=2 \\ \overline{-7,-7}=0 \\\overline{1,-5}=6 \\ \overline{1,-7}=8 } \Rightarrow \overline{CD} \ne 4,故選\bbox[red,2pt]{(C)}$$
解:$${\sqrt 9\over \sqrt {12}} \div \sqrt{54\over 12}\times \sqrt{3\over 6} =\sqrt{ 9\over 12} \div \sqrt{54\over 12}\times \sqrt{3\over 6}=\sqrt{ 3\over 4} \div \sqrt{9\over 2}\times \sqrt{1\over 2} \\= \sqrt{{3\over 4}\times {2\over 9}\times {1\over 2}} =\sqrt{{1\over 4}\times {1\over 3}} =\sqrt{1\over 12}={1\over 2\sqrt 3} ={\sqrt 3\over 6},故選\bbox[red,2pt]{(B)}$$
解:
六邊形ABCDEF有6個小三角形,三角形FCG有4個小三角形,所以兩者面積比6:4=3:2,故選(D)。
解:
$$假設方格子邊長為a \Rightarrow \cases{正方形ABCD=4a\times 4a=16a^2 \\\triangle ADE={1\over 2}\times 4a\times 2a=4a^2 \\ \triangle BEF={1\over 2}\times 2a\times 3a=3a^2 \\ \triangle CDF={1\over 2}\times a\times 4a=2a^2 } \\ \Rightarrow \triangle DEF = 16a^2-4a^2-3a^2-2a^2= 7a^2 ={21\over 4} \Rightarrow a^2={3\over 4} \Rightarrow 16a^2=12,故選\bbox[red,2pt]{(B)}$$
解:$$\begin{array}{l|cc} 抓到糖果數 & 5 & 6 & 7 & 8 & 9 & 10& 11&12 &13 & 14& 15\\\hline 次數& 3 & 7 & 6 & 10 &11 & 8 & 13 & 7 & 1& 4 & 2\\\hline 累積次數 & 3 & 10 & 16 & 26 & 37 & 45 & 58 & 65 & 66 & 70& 72\\\hline \end{array} \\ 總人數為72,中位數為第36人與第37人抓到糖果的平均數\\,由上表累積次數可知第36人與第37人抓到的糖果數皆為9,即a=9;\\又抓到11個糖果的人數最多(13人),所以b=11;因此a+b=9+11=20,故選\bbox[red,2pt]{(A)}$$
解:
利用長除法
餘式為 3x-3,故選(D)。
取兩支籤共有4X3=12種可能,兩號碼和為奇數的情況(1,2), (1,4), (2,1), (2,3), (3, 2), (3,4), (4,1), (4,3),共有8種情況,所以機率為8/12=2/3,故選(B)。
解:
$$\overset{\Large{\frown}}{AB}: \overset{\Large{\frown}}{BC}: \overset{\Large{\frown}}{CA} = \angle C:\angle A: \angle B= 12:13 :11 \\\Rightarrow \cases{\angle A=360^\circ \times 13/(11+12+13) \div 2= 65^\circ \\\angle B=360^\circ \times 11/(11+12+13) \div 2= 55^\circ \\\angle C=360^\circ \times 12/(11+12+13) \div 2= 60^\circ }; 又平行線之內錯角相等\\,因此 \cases{\overline{AB} \parallel \overline{DF} \Rightarrow \angle DFE =\angle B=55^\circ\\ \overline{AC} \parallel \overline{DE} \Rightarrow \angle EDF =\angle C=120^\circ } \Rightarrow \angle EDF=\angle A=65^\circ,故選\bbox[red,2pt]{(C)}$$
解:
兩圓相交於兩點,所以兩圓半徑之和需大於13,因此(C)(D)不合。且大圓半徑減小圓半徑需小於13,因此(A)不合。故選(B)。
解:
解:
$$假設底面梯形邊長為a,b,c,d及直角柱高為h,則\cases{底面面積A=16\div 2 =8\\ 側面面積和=(a+b+c+d)h=45\\ 體積=A\times h=24} \\\Rightarrow \cases{A=8\\ h=3\\ a+b+c+d=15} \Rightarrow 邊長長度和=4h+2(a+b+c+d) =12+30=42,故選\bbox[red,2pt]{(C)}$$解:
由圖形可知,y的最大值在x軸之上,所以最大值大於0
令\(y=f(x)\),由圖形可知,\(f(1)<f(0)<f(-1)=1\)。
所以只有(D)正確,故選\(\bbox[red,2pt]{(D)}\)。
解:
假設兩人均在O點,小龍向北直走160公尺至A點,再向東80公尺至B點(神仙百貨);阿虎由O點向西直走x公尺至C點,使得\(\overline{BC}=340\),如上圖。
由直角三角形BCD可知1602+(80+x)2=3402⇒x2+160x-8360=0 ⇒(x-220)(x+380)=0 ⇒x=220,故選(C)。
假設兩人均在O點,小龍向北直走160公尺至A點,再向東80公尺至B點(神仙百貨);阿虎由O點向西直走x公尺至C點,使得\(\overline{BC}=340\),如上圖。
由直角三角形BCD可知1602+(80+x)2=3402⇒x2+160x-8360=0 ⇒(x-220)(x+380)=0 ⇒x=220,故選(C)。
解:
 $$\cases{\angle A=30^\circ \\ \overline{AB}=\overline{AC}} \Rightarrow \angle B=\angle C= (180^\circ-30^\circ)\div 2= 75^\circ;\\又\overline{BC} =\overline{BD} \Rightarrow \angle BDC=\angle C=75^\circ \Rightarrow \angle DBC= 180^\circ-2\times 75^\circ=30^\circ\\ \Rightarrow \angle EBD= 75^\circ-30^\circ =45^\circ\\ 同理,\overline{BD} =\overline{BE} \Rightarrow \angle BDE= \angle BED =(180^\circ-45^\circ) \div 2=67.5^\circ,故選\bbox[red,2pt]{(C)}$$
$$\cases{\angle A=30^\circ \\ \overline{AB}=\overline{AC}} \Rightarrow \angle B=\angle C= (180^\circ-30^\circ)\div 2= 75^\circ;\\又\overline{BC} =\overline{BD} \Rightarrow \angle BDC=\angle C=75^\circ \Rightarrow \angle DBC= 180^\circ-2\times 75^\circ=30^\circ\\ \Rightarrow \angle EBD= 75^\circ-30^\circ =45^\circ\\ 同理,\overline{BD} =\overline{BE} \Rightarrow \angle BDE= \angle BED =(180^\circ-45^\circ) \div 2=67.5^\circ,故選\bbox[red,2pt]{(C)}$$

















































第4題無解吧..
回覆刪除與題本的圖有微妙的差距
刪除只有(D)最有可能,其他都不像線對稱~~
刪除D也是錯誤的
回覆刪除最後一題有地方寫錯了,"三角形OAD"寫錯了。
回覆刪除24題也寫錯了,是角DEF=角C。
回覆刪除感恩!
回覆刪除