朱式幸福: 105年桃連區內壢高中特招數學詳解

試題來源：內壢高中

解：

(A) A與原點距離小於1
(B) 絕對值必大於等於0
(C) 0<a<1, b<-2, 所以a+b<0
(D) 0<a<1, b<-2, 所以a-b>0
，故選$\bbox[red,2pt]{(D)}$。

解：

三者顯然相同，故選$\bbox[red,2pt]{(A)}$。

解：
$${(3x+2)}^2={(5x-6)}^2\Rightarrow 9x^2+12x+4=25x^2-60x+36\\ \Rightarrow 16x^2-72x+32=0 \Rightarrow 2x^2-9x+4=0\Rightarrow (2x-1)(x-4)=0\\ \Rightarrow x=4 平方根只有1個14，x=\frac{1}{2}平方根為\pm\frac{7}{2}，故選\bbox[red,2pt]{(C)}。$$

解：

重點：同時偵測到，同時消失
相同時間內，甲飛機飛行距離為$\overline{BC}$、乙飛機飛行距離為$\overline{AD}$，如上圖。$\overline{BC}=120，\overline{AD}=160$，相同時間的飛行距離比等於速度比，即甲:乙=120:160=3:4，故選$\bbox[red,2pt]{(A)}$。

解：

灰色面積=${(a+4)}^2-{(a+1)}^2=6a+15$；灰色短邊長度=(a+4)-(a+1)=3，因此6a+15=3k，k=2a+5，故選$\bbox[red,2pt]{(A)}$。

解：

ABCD周長=36，即2(x+y)=36；
$\triangle ABP周長=a+b+x, \triangle BCP周長=a+b+y$，兩者相差6，即a+b+x+6=a+b+y$\Rightarrow y-x=6$，故選$\bbox[red,2pt]{(B)}$。

解：
上午11:00至下午3:50(15:50)，共計4小時50分鐘=290分鐘。每40分鐘印90張紙，290分鐘可印290分鐘=7次40分鐘再加10分鐘，因此可印$90\times 30\times 7+90\times 10 = 19800$，故選$\bbox[red,2pt]{(C)}$。

解：

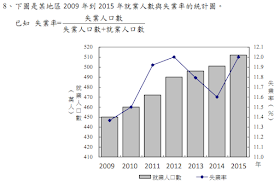
2009至2012年，失業率逐年升高，但2012至2014年逐年下降，因此失業率並無逐年增加，故選$\bbox[red,2pt]{(C)}$。此外，2015年失業人數x, $\frac{x}{x+510}=0.12\Rightarrow x=69.5$，2012年失業人數y, $\frac{y}{y+490}=0.12\Rightarrow y=66.8$，2015年失業人口比2012年少。相同的失業率，就業人口多，失業人口就比較少。

解：

$$令\angle NOB=a\Rightarrow \angle NOM=2a, \angle MOA=6a\Rightarrow a+2a+6a=180\\ \Rightarrow a=20\Rightarrow \angle NOM=2a=40，故選\bbox[red,2pt]{(C)}。$$

解：

$$\begin{cases} a-b+6=-1 \\ 7-3b=4 \end{cases}\Rightarrow \begin{cases} a=-6 \\ b=1 \end{cases}\Rightarrow a-b=-6-1=-7，故選\bbox[red,2pt]{(D)}。$$

解：

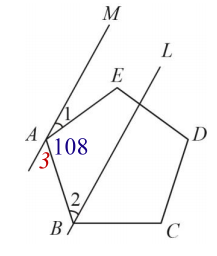
$$M//L\Rightarrow \angle 2=\angle 3\Rightarrow \angle 1= 180^\circ-\angle 3-108^\circ(正五邊形內角為108^\circ)\\=72^\circ-45^\circ=27^\circ，故選\bbox[red,2pt]{(A)}。$$

解：

$$P經過y=2x\Rightarrow 2=2m\Rightarrow m=1；又P(1,2)經過y=ax+4\Rightarrow 2=a+4\Rightarrow a=-2\\ 2x<ax+4\Rightarrow 2x<-2x+4\Rightarrow 4x<4\Rightarrow x<1，故選\bbox[red,2pt]{(B)}。$$

解：$$a={25}^7+5^{13}={5^2}^7+5^{13}=5^{14}+5^{13}=5^{13}(5+1)=5^{12}\times 5 \times 2\times 3，故選\bbox[red,2pt]{(B)}。$$

解：
假設正方形每邊有a個硬幣，則三角形每邊有a+2個硬幣。
正方形有$a^2$個硬幣，三角形有$\frac{(a+3)(a+2)}{2}$個硬幣，兩者相同，即$${ a }^{ 2 }=\frac { \left( a+3 \right) \left( a+2 \right) }{ 2 } \Rightarrow 2{ a }^{ 2 }={ a }^{ 2 }+5a+6\Rightarrow { a }^{ 2 }-5a-6=0\\ \Rightarrow (a-6)(a+1)=0\Rightarrow a=6\Rightarrow 硬幣共有{ a }^{ 2 }=36個，故選\bbox[red,2pt]{(C)}。$$

解：
$${ x }^{ 3 }+3{ x }^{ 2 }-x+2016=\left[ x\left( { x }^{ 2 }+2x-3 \right) \right] +\left[ { x }^{ 2 }+2x \right] +2016=\left[ 0 \right] +\left[ 3 \right] +2016\\=2019，故選\bbox[red,2pt]{(A)}。$$

解：
$$\begin{cases} \left| x \right| +\left| y \right| =2 \\ \left| y \right| =\left| x \right| +1 \end{cases}\Rightarrow \begin{cases} x-y=2 \\ -y=x+1 \end{cases}\Rightarrow x=\frac { 1 }{ 2 } ,y=\frac { -3 }{ 2 } ，故選\bbox[red,2pt]{(C)}。$$

解：

$$直角\triangle OMD中, \overline{OD}=半徑=13, \overline{MD}=\overline{CD}/2=12\Rightarrow \overline{OM}=5\\同理，直角\triangle OAN\Rightarrow \overline{ON}=12\Rightarrow \overline{MN}=\overline{ON}-\overline{OM}=12-5=7，故選\bbox[red,2pt]{(B)}。$$

解：
$$若\overline{DA}=3，則\overline{DA}+\overline{AB}+\overline{BC}=\overline{CD}，表示D、A、B、C呈一直線，\\無法形成四邊形，故選\bbox[red,2pt]{(A)}。$$

解：

依題意可知: a, b 為$x^2-2x-b=0$之相異兩根，因此兩根之和=2，故選$\bbox[red,2pt]{(A)}$。

解：

$$令\overline{EC}=a，則\overline{BE}=2-a；由於\overline{DE}為中垂線\Rightarrow \overline{EA}=\overline{EC}\\ 直角\triangle ABE中，{\overline{AE}}^2={\overline{AB}}^2+ {\overline{BE}}^2\Rightarrow a^2=1+{(2-a)}^2\Rightarrow 4a=5 \Rightarrow a=\frac{5}{4}\\ \overline{EC}為\triangle DEC 外接圓的直徑\Rightarrow 半徑=\frac{\overline{EC}}{2}=\frac{5}{8}，故選\bbox[red,2pt]{(D)}。$$

解：

$$原圖形 y=x^2-4x+a\Rightarrow y+4-a={(x-2)}^2，\\新圖形y=x^2-10x+b\Rightarrow y-b+25={(x-5)}^2\\ 向上平移6單位\Rightarrow 4-a-6=25-b\Rightarrow b-a=25+6-4=27，故選\bbox[red,2pt]{(C)}。$$

解：
$$\begin{cases} b=a+2 \\ c=b+2=a+4 \\ d=c+2=a+6 \end{cases}且\overline { AB } =\overline { CD } \Rightarrow c+d=b+2a\Rightarrow 2a+10=3a+2\Rightarrow a=8\\ \Rightarrow ABCD面積=\overline { AB } \times \overline { AD } =\left( c+d \right) \left( b+c \right) =\left( 2a+10 \right) \left( 2a+6 \right)\\ =26\times 22=572，故選\bbox[red,2pt]{(A)}。$$

解：
假設評審有a人，則參賽人數為3a-6$\Rightarrow a(3a-6)=144 \Rightarrow a=8 \Rightarrow$ (3a-6)-a=2a-6=16-6=10，故選$\bbox[red,2pt]{(B)}$。

解：

假設木製書架有a個，鐵製書架有15-a個。依題意可知：$$31<\frac { 409-20a }{ 15-a } <33\Rightarrow \begin{cases} 409-20a<33(15-a) \\ 31(15-a)<409-20a \end{cases}\Rightarrow \frac{56}{11}<a<\frac { 86 }{ 13 } \\ \Rightarrow a=6，故選\bbox[red,2pt]{(C)}。$$

解：

$$令\angle BDC=x, \angle ACD=a；\overline{AD}=\overline{AC}\\ \Rightarrow \angle ACD=\angle ADC \Rightarrow \angle ADB=a-x, \angle DAC=180-2a\\ \overline{AD}= \overline{AB}\Rightarrow \angle ABD=\angle ADB=a-x\\ \triangle ABD\Rightarrow \angle A+\angle ABD+\angle ADB=180\Rightarrow (60+180-2a)+2(a-x)=180\\ \Rightarrow x=30，故選\bbox[red,2pt]{(B)}。$$

解：

第1天開出3之後的三天如上圖，第四天出現3有2種可能，其機率為2/8=1/4，故選$\bbox[red,2pt]{(C)}$。

解：

$$\triangle ABC\cong\triangle CDA\Rightarrow \triangle ABC:\triangle CDA=1:1\\H為\triangle ADC重心\triangle AHO:\triangle CDA=1:6；同理 \triangle AGO:\triangle ABC=1:6\\ \Rightarrow \triangle AGH:\triangle ABC=1:3，故選\bbox[red,2pt]{(B)}。$$

解：
$$2{ a }^{ 2 }+2b^{ 2 }+2c^{ 2 }+2d^{ 2 }=2ab+2bc+2cd+2da\\ \Rightarrow \left[ a^{ 2 }-2ab+b^{ 2 } \right] +\left[ b^{ 2 }-2bc+c^{ 2 } \right] +\left[ c^{ 2 }-2cd+d^{ 2 } \right] +\left[ d^{ 2 }-2da+a^{ 2 } \right] =0\\ \Rightarrow { \left( a-b \right) }^{ 2 }+{ \left( b-c \right) }^{ 2 }+{ \left( c-d \right) }^{ 2 }+{ \left( d-a \right) }^{ 2 }=0\\ \Rightarrow a=b=c=d，故選\bbox[red,2pt]{(C)}。$$

解：

$$\overline{AG}=2且\triangle ADG=4\Rightarrow \overline{GD}=4；\overline{AB}= \overline{ED}=10\Rightarrow \overline{EG}=10-\overline{GD}=6\\ \triangle GAD\sim\triangle GCE\Rightarrow \frac{\overline{AG}}{\overline{GD}}=\frac{\overline{GC}}{\overline{GE}}\Rightarrow \overline{GC}=3\\ 梯形DGCF=\frac{(\overline{GC}+\overline{DF}= \overline{AC})(\overline{DG})}{2}=\frac{(3+5)\times 4}{2}=16，故選\bbox[red,2pt]{(D)}。$$

解：

$$\overline{CD}//\overline{OB}\Rightarrow \angle OCD=\angle EOC=30^\circ；\\\angle DCO=\angle DOC=30^\circ \Rightarrow \overline{DC}=\overline{OD}=4\\ 作\overline{CF}\bot\overline{OA}\Rightarrow \overline{CE}=\overline{CF}=\overline{CD}\times \frac{\sqrt{3}}{2}=2\sqrt{3}，故選\bbox[red,2pt]{(B)}。$$