104年專科學校畢業程度自學進修學力鑑定考試
專業科目(一)：微積分 詳解
解：$$\lim_{x\to0^-}{[3+x]}=[2.x]=2 \Rightarrow 故選：\bbox[red,2pt]{(B)}$$
解：$$\begin{cases} \sqrt { x-3 } \ge 0 \\ \sqrt { x-1 } >0 \end{cases}\Rightarrow \begin{cases} x\ge 3 \\ x>1 \end{cases}\Rightarrow x\ge 3\Rightarrow x\in [3,\infty )\Rightarrow 故選\bbox[red,2pt]{(D)}$$
解：連續不一定可微，但可微一定連續，故選\(\bbox[red,2pt]{(D)}\)
解：$$f\left( x \right) =\frac { 2 }{ x^{ 2 }-1 } =\frac { 2 }{ \left( x-1 \right) \left( x+1 \right) } =\frac { 1 }{ x-1 } -\frac { 1 }{ x+1 } \\ \Rightarrow f'\left( x \right) =\frac { -1 }{ { \left( x-1 \right) }^{ 2 } } +\frac { 1 }{ { \left( x+1 \right) }^{ 2 } } \Rightarrow f''\left( x \right) =\frac { 2 }{ { \left( x-1 \right) }^{ 3 } } -\frac { 2 }{ { \left( x+1 \right) }^{ 3 } } \\ \Rightarrow f'''\left( x \right) =\frac { -6 }{ { \left( x-1 \right) }^{ 4 } } +\frac { 6 }{ { \left( x+1 \right) }^{ 4 } } \Rightarrow f^{ (4) }\left( x \right) =\frac { 24 }{ { \left( x-1 \right) }^{ 5 } } -\frac { 24 }{ { \left( x+1 \right) }^{ 5 } } \\ \Rightarrow f^{ (4) }\left( 2 \right) =24-\frac { 24 }{ { 3 }^{ 5 } } =24\left( 1-\frac { 1 }{ { 3 }^{ 5 } } \right) \Rightarrow 故選\bbox[red,2pt]{(B)}$$
解：$$h\left( x \right) ={ x }^{ \sin { x } }={ e }^{ \ln { x } \sin { x } }\Rightarrow h'\left( x \right) ={ e }^{ \ln { x } \sin { x } }\left( \ln { x } \sin { x } \right) '={ x }^{ \sin { x } }\left( \frac { \sin { x } }{ x } +\ln { x } \cos { x } \right) \\ \Rightarrow h'\left( 1 \right) =1\times \left( \sin { 1 } +0 \right) =\sin { 1 } \Rightarrow 故選\bbox[red,2pt]{(C)}$$
解：$$\frac { xf\left( 1 \right) -f\left( x \right) }{ x-1 } =\frac { \left( x-1 \right) f\left( 1 \right) +f\left( 1 \right) -f\left( x \right) }{ x-1 } =f\left( 1 \right) -\frac { f\left( x \right) -f\left( 1 \right) }{ x-1 } \\ \Rightarrow \lim _{ x\to 1 }{ \frac { xf\left( 1 \right) -f\left( x \right) }{ x-1 } } =f\left( 1 \right) -\lim _{ x\to 1 }{ \frac { f\left( x \right) -f\left( 1 \right) }{ x-1 } } =f\left( 1 \right) -f'\left( 1 \right) =2-3=-1 \\ \Rightarrow 故選\bbox[red,2pt]{(B)}$$
解：$$x+\sqrt { y } =y+\sqrt { x } \Rightarrow 1+\frac { \frac { dy }{ dx } }{ 2\sqrt { y } } =\frac { dy }{ dx } +\frac { 1 }{ 2\sqrt { x } } \Rightarrow 1-\frac { 1 }{ 2\sqrt { x } } =\frac { dy }{ dx } -\frac { \frac { dy }{ dx } }{ 2\sqrt { y } } \\ \Rightarrow \frac { dy }{ dx } =\frac { 1-\frac { 1 }{ 2\sqrt { x } } }{ 1-\frac { 1 }{ 2\sqrt { y } } } \Rightarrow \left. \frac { dy }{ dx } \right| _{ (1,1) }=\frac { 1-\frac { 1 }{ 2 } }{ 1-\frac { 1 }{ 2 } } =1 \Rightarrow 故選\bbox[red,2pt]{(A)}$$
解：$$f_{ 1 }\left( 0 \right) 不存在;f_{ 2 }\left( 0 \right) 不存在;f_{ 3 }\left( -1 \right) 不存在;\Rightarrow 故選\bbox[red,2pt]{(D)} $$
解：$$f\left( x \right) ={ x }^{ \frac { 7 }{ 5 } }+{ x }^{ \frac { 2 }{ 5 } }\Rightarrow f'\left( x \right) =\frac { 7 }{ 5 } { x }^{ \frac { 2 }{ 5 } }+\frac { 2 }{ 5 } { x }^{ -\frac { 3 }{ 5 } }\Rightarrow f''\left( x \right) =\frac { 14 }{ 25 } { x }^{ -\frac { 3 }{ 5 } }-\frac { 6 }{ 25 } { x }^{ -\frac { 8 }{ 5 } }\\ f''\left( x \right) =0\Rightarrow \frac { 14 }{ 25 } { x }^{ -\frac { 3 }{ 5 } }-\frac { 6 }{ 25 } { x }^{ -\frac { 8 }{ 5 } }=0\Rightarrow \frac { 2 }{ 25 } { x }^{ -\frac { 8 }{ 5 } }\left( 7{ x }-3 \right) =0\Rightarrow x=0,\frac { 3 }{ 7 } \Rightarrow 故選\bbox[red,2pt]{(C)}$$
解：$$f\left( x \right) =x+\frac { 1 }{ x^{ 2 } } \Rightarrow f'\left( x \right) =1-\frac { 2 }{ x^{ 3 } } \Rightarrow f''\left( x \right) =\frac { 6 }{ x^{ 4 } } \\ f'\left( x \right) =0\Rightarrow 1-\frac { 2 }{ x^{ 3 } } =0\Rightarrow x=\sqrt [ 3 ]{ 2 } \Rightarrow f''\left( \sqrt [ 3 ]{ 2 } \right) >0\\ \Rightarrow x=\sqrt [ 3 ]{ 2 } 有相對極小值f\left( \sqrt [ 3 ]{ 2 } \right) =\sqrt [ 3 ]{ 2 } +\frac { 1 }{ \sqrt [ 3 ]{ 4 } } =\frac { 3 }{ \sqrt [ 3 ]{ 4 } } \Rightarrow 故選\bbox[red,2pt]{(D)}$$
解：$$\because \lim _{ x\to 0^{ + } }{ \frac { { x }^{ 2 } }{ \sin ^{ 2 }{ x } } } =\lim _{ x\to 0^{ + } }{ \frac { 2x }{ 2\sin { x } \cos { x } } } =\lim _{ x\to 0^{ + } }{ \frac { 2x }{ \sin { 2x } } } =\lim _{ x\to 0^{ + } }{ \frac { 2 }{ 2\cos { 2x } } } =1\\ \therefore \lim _{ x\to 0^{ + } }{ \frac { { x^{ 3 } }\sin { \frac { 1 }{ x^{ 2 } } } }{ \sin ^{ 2 }{ x } } } =\lim _{ x\to 0^{ + } }{ \left( \left( x\sin { \frac { 1 }{ x^{ 2 } } } \right) \left( \frac { { x^{ 2 } } }{ \sin ^{ 2 }{ x } } \right) \right) } =\lim _{ x\to 0^{ + } }{ \left( x\sin { \frac { 1 }{ x^{ 2 } } } \right) } \cdot \lim _{ x\to 0^{ + } }{ \left( \frac { { x^{ 2 } } }{ \sin ^{ 2 }{ x } } \right) } =\lim _{ x\to 0^{ + } }{ \left( x\sin { \frac { 1 }{ x^{ 2 } } } \right) } \\ -\left| x \right| \le \left| x\sin { \frac { 1 }{ x^{ 2 } } } \right| \le \left| x \right| \Rightarrow \lim _{ x\to 0^{ + } }{ \left( x\sin { \frac { 1 }{ x^{ 2 } } } \right) } =0\Rightarrow \lim _{ x\to 0^{ + } }{ \frac { { x^{ 3 } }\sin { \frac { 1 }{ x^{ 2 } } } }{ \sin ^{ 2 }{ x } } } =0\Rightarrow 故選\bbox[red,2pt]{(B)}$$
解：$$f'\left( t \right) =\sqrt { 1+t^{ 3 } } \Rightarrow \frac { d }{ dx } \int _{ x^{ 2 } }^{ x^{ 3 } }{ \sqrt { 1+t^{ 3 } } } dt=\frac { d }{ dx } \int _{ x^{ 2 } }^{ x^{ 3 } }{ f'\left( t \right) } dt=\frac { d }{ dx } \left( f\left( x^{ 3 } \right) -f\left( x^{ 2 } \right) \right) \\ =f'\left( x^{ 3 } \right) \times 3x^{ 2 }-f'\left( x^{ 2 } \right) \times 2x=3x^{ 2 }\sqrt { 1+x^{ 9 } } -2x\sqrt { 1+x^{ 6 } } \Rightarrow 故選\bbox[red,2pt]{(C)}$$
解：$$u=\sqrt { x^{ 2 }-1 } \Rightarrow \begin{cases} du=\frac { x }{ \sqrt { x^{ 2 }-1 } } dx \\ u^{ 2 }+1=x^{ 2 } \end{cases}\Rightarrow \int { \frac { 1 }{ x\sqrt { x^{ 2 }-1 } } dx } =\int { \frac { 1 }{ u^{ 2 }+1 } du } \\ \Rightarrow \int _{ \sqrt { 2 } }^{ 2 }{ \frac { 1 }{ x\sqrt { x^{ 2 }-1 } } } dx=\int _{ 1 }^{ \sqrt { 3 } }{ \frac { 1 }{ u^{ 2 }+1 } } du=\left. \left[ \arctan { u } \right] \right| ^{ \sqrt { 3 } }_{ 1 }=\frac { \pi }{ 3 } -\frac { \pi }{ 4 } =\frac { \pi }{ 12 } \Rightarrow 故選\bbox[red,2pt]{(D)} $$
解：
依積分的定義，本題相當於求\(y=\frac{1}{x}\)與\(x\)軸之間的面積，且\(x\in [2,3]\)，即$$\lim _{ n\to \infty }{ \left( \sum _{ i=1 }^{ n }{ \frac { 1 }{ 2+\frac { i }{ n } } } \right) \frac { 1 }{ n } } =\lim _{ n\to \infty }{ \left( \sum _{ i=1 }^{ n }{ f\left( 2+\Delta x\times i \right) } \times \Delta x \right) } ,其中\Delta x=\frac { 1 }{ n } ,f\left( x \right) =\frac { 1 }{ x } \\ =\int _{ 2 }^{ 3 }{ \frac { 1 }{ x } } dx=\left. \left[ \ln { x } \right] \right| ^{ 3 }_{ 2 }=\ln { 3 } -\ln { 2 } \Rightarrow 故選\bbox[red,2pt]{(C)}$$
解：$$f\left( x \right) =\ln { \frac { \left( x+1 \right) \cdot \sqrt [ 3 ]{ x+3 } }{ { \left( x+9 \right) }^{ 5 } } } \Rightarrow f'\left( x \right) =\frac { { \left( x+9 \right) }^{ 5 } }{ \left( x+1 \right) \cdot \sqrt [ 3 ]{ x+3 } } \times \frac { d }{ dx } \left( \frac { \left( x+1 \right) \cdot \sqrt [ 3 ]{ x+3 } }{ { \left( x+9 \right) }^{ 5 } } \right) \\ =\frac { { \left( x+9 \right) }^{ 5 } }{ \left( x+1 \right) \cdot \sqrt [ 3 ]{ x+3 } } \left( \frac { \sqrt [ 3 ]{ x+3 } +\frac { x+1 }{ 3{ \left( x+3 \right) }^{ \frac { 2 }{ 3 } } } }{ { \left( x+9 \right) }^{ 5 } } -\frac { 5\left( x+1 \right) \cdot \sqrt [ 3 ]{ x+3 } }{ { \left( x+9 \right) }^{ 6 } } \right) \\ \Rightarrow f'\left( 0 \right) =\frac { { 9 }^{ 5 } }{ \sqrt [ 3 ]{ 3 } } \left( \frac { \sqrt [ 3 ]{ 3 } +\frac { 1 }{ 3\sqrt [ 3 ]{ 9 } } }{ { 9 }^{ 5 } } -\frac { 5\sqrt [ 3 ]{ 3 } }{ { 9 }^{ 6 } } \right) =\frac { \sqrt [ 3 ]{ 3 } +\frac { 1 }{ 3\sqrt [ 3 ]{ 9 } } }{ \sqrt [ 3 ]{ 3 } } -\frac { 5\sqrt [ 3 ]{ 3 } }{ { 9\sqrt [ 3 ]{ 3 } } } =1+\frac { 1 }{ 9 } -\frac { 5 }{ 9 } =\frac { 5 }{ 9 } \Rightarrow 故選\bbox[red,2pt]{(B)} $$
解：$$\int _{ 0 }^{ \frac { \pi }{ 4 } }{ \sec { x } dx } =\left. \left[ \ln { \left| \sec { x } +\tan { x } \right| } \right] \right| ^{ \frac { \pi }{ 4 } }_{ 0 }=\ln { \left( \sqrt { 2 } +1 \right) } -\ln { \left( 1 \right) } =\ln { \left( \sqrt { 2 } +1 \right) } \Rightarrow 故選\bbox[red,2pt]{(C)}$$
解：$$\int { \frac { 1 }{ x^{ 2 }+2x+10 } } dx=\int { \frac { 1 }{ 9+\left( x^{ 2 }+2x+1 \right) } } dx=\int { \frac { 1 }{ 9+{ \left( x+1 \right) }^{ 2 } } } dx=\int { \frac { 1 }{ 9\left( 1+{ \left( \frac { x+1 }{ 3 } \right) }^{ 2 } \right) } } dx\\ =\frac { 1 }{ 3 } \arctan { \frac { x+1 }{ 3 } } +C \Rightarrow 故選\bbox[red,2pt]{(A)}$$
解：$$\int { \sin { 2x } \cos { x } } dx=\int { 2\sin { x } \cos ^{ 2 }{ x } } dx=\int { 2\sin { x } \left( 1-\sin ^{ 2 }{ x } \right) } dx=2\int { \sin { x } } dx-2\int { \sin ^{ 3 }{ x } } dx\\ =-2\cos { x } -2\left( -\frac { 1 }{ 3 } \sin ^{ 2 }{ x } \cos { x } -\frac { 2 }{ 3 } \cos { x } \right) +C=\frac { 2 }{ 3 } \sin ^{ 2 }{ x } \cos { x } -\frac { 2 }{ 3 } \cos { x } +C\\ =\frac { 2 }{ 3 } \cos { x } \left( \sin ^{ 2 }{ x } -1 \right) +C=\frac { 2 }{ 3 } \cos { x } \left( -\cos ^{ 2 }{ x } \right) +C=-\frac { 2 }{ 3 } \cos ^{ 3 }{ x } +C\\ =-\frac { 2 }{ 3 } \left( \frac { 1 }{ 4 } \cos { 3x } +\frac { 3 }{ 4 } \cos { x } \right) +C=-\frac { 1 }{ 6 } \cos { 3x } -\frac { 1 }{ 2 } \cos { x } +C\Rightarrow故選\bbox[red,2pt]{(D)}$$
解：$$\int _{ 0 }^{ 1 }{ \left( f\left( x \right) -g\left( x \right) \right) } dx=\int _{ 0 }^{ 1 }{ \left( -2x^{ 2 }+2x \right) } dx=\left. \left[ -\frac { 2 }{ 3 } x^{ 3 }+x^{ 2 } \right] \right| ^{ 1 }_{ 0 }=\frac { 1 }{ 3 } \Rightarrow故選\bbox[red,2pt]{(B)}$$
解：$$x=\sqrt { x } \Rightarrow x^{ 2 }-x=0\Rightarrow x(x-1)=0\Rightarrow x=0,1\\ \int _{ x=0 }^{ x=1 }{ { \left( \sqrt { x } \right) }^{ 2 }\pi } dx-\int _{ x=0 }^{ x=1 }{ { \left( x^{ 2 } \right) }\pi } dx=\pi \left( \left. \left[ \frac { 1 }{ 2 } x^{ 2 } \right] \right| ^{ 1 }_{ 0 }-\left. \left[ \frac { 1 }{ 3 } x^{ 3 } \right] \right| ^{ 1 }_{ 0 } \right) =\pi \left( \frac { 1 }{ 2 } -\frac { 1 }{ 3 } \right) =\frac { \pi }{ 6 } \Rightarrow故選\bbox[red,2pt]{(D)} $$
解：
\(x=5,y=-12\Rightarrow r=\sqrt{x^2+y^2}=\sqrt{25+144}=13\)
\(\sin{\theta}=\frac{-12}{13},\cos{\theta}=\frac{5}{13},\tan{\theta}=\frac{-12}{5}\)
故選\(\bbox[red,2pt]{(C)}\)
解：$$\lim _{ n\to \infty }{ \ln { { \left( 1+\frac { 1 }{ n } \right) }^{ n } } } =\lim _{ n\to \infty }{ \ln { { \left( \frac { n+1 }{ n } \right) }^{ n } } } =\lim _{ n\to \infty }{ n\cdot \ln { { \left( \frac { n+1 }{ n } \right) } } } =\lim _{ n\to \infty }{ \frac { \ln { { \left( \frac { n+1 }{ n } \right) } } }{ \frac { 1 }{ n } } } \\ =\lim _{ n\to \infty }{ \frac { \left( \frac { n }{ n+1 } \right) \left( -\frac { 1 }{ n^{ 2 } } \right) }{ -\frac { 1 }{ n^{ 2 } } } } =\lim _{ n\to \infty }{ \frac { n }{ n+1 } } =1 \Rightarrow故選\bbox[red,2pt]{(A)} $$
解：$$\sum _{ k=1 }^{ \infty }{ \frac { 2k+1 }{ { k }^{ 2 }{ \left( k+1 \right) }^{ 2 } } } =\sum _{ k=1 }^{ \infty }{ \left( \frac { 1 }{ { k }^{ 2 } } -\frac { 1 }{ { \left( k+1 \right) }^{ 2 } } \right) } =\left( \frac { 1 }{ 1 } -\frac { 1 }{ { 2 }^{ 2 } } \right) +\left( \frac { 1 }{ { 2 }^{ 2 } } -\frac { 1 }{ { 3 }^{ 2 } } \right) +\left( \frac { 1 }{ { 3 }^{ 2 } } -\frac { 1 }{ { 4 }^{ 2 } } \right) +\cdots \\=1\Rightarrow故選\bbox[red,2pt]{(B)} $$
解：$$xy+z^{ 3 }x-2yz=0\Rightarrow y+3z^{ 2 }\frac { \partial z }{ \partial x } x+z^{ 3 }-2y\frac { \partial z }{ \partial x } =0\Rightarrow \frac { \partial z }{ \partial x } =\frac { y+z^{ 3 } }{ 2y-3z^{ 2 } } \\ \Rightarrow \left. \frac { \partial z }{ \partial x } \right| _{ (1,1,1) }=\frac { 1+1 }{ 2-3 } =-2\Rightarrow故選\bbox[red,2pt]{(D)} $$
解：$$由\begin{cases} x=r\cos { \theta } \\ y=r\sin { \theta } \end{cases}\Rightarrow \iint { x^{ 2 }+y^{ 2 } } dydx=\iint { r^{ 2 }r } drd\theta =\iint { r^{ 3 } } drd\theta \\ 及\begin{cases} 0\le x\le \sqrt { 1-x^{ 2 } } \\ 0\le y\le 1 \end{cases}\Rightarrow \begin{cases} 0\le x^{ 2 }+y^{ 2 }\le 1 \\ 0\le x,y\le 1 \end{cases}\Rightarrow \begin{cases} 0\le r\le 1 \\ 0\le \theta \le \frac { \pi }{ 2 } \end{cases}\\ 可知\int _{ 0 }^{ 1 }{ \int _{ 0 }^{ \sqrt { 1-x^{ 2 } } }{ x^{ 2 }+y^{ 2 } } } dydx=\int _{ 0 }^{ \frac { \pi }{ 2 } }{ \int _{ 0 }^{ 1 }{ r^{ 3 } } } drd\theta =\int _{ 0 }^{ \frac { \pi }{ 2 } }{ \left. \left[ \frac { 1 }{ 4 } r^{ 4 } \right] \right| ^{ 1 }_{ 0 } } d\theta \\ =\int _{ 0 }^{ \frac { \pi }{ 2 } }{ \frac { 1 }{ 4 } } d\theta =\left. \left[ \frac { 1 }{ 4 } \theta \right] \right| ^{ \frac { \pi }{ 2 } }_{ 0 }=\frac { \pi }{ 8 } , 故選\bbox[red,2pt]{(D)}$$
解：$$\lim _{ x\to -2 }{ \sqrt [ 3 ]{ x^{ 2 }+4x-4 } } =\sqrt [ 3 ]{ (-2)^{ 2 }+4\cdot (-2)-4 } =\sqrt [ 3 ]{ -8 } =-2, 故選\bbox[red,2pt]{(C)}$$
解：$$\lim _{ x\to \pm \infty }{ \frac { x-5 }{ x^{ 2 }-x-2 } } =0\Rightarrow y=0為水平漸近線, 故選\bbox[red,2pt]{(B)}$$
解：$$2\times 1+1=1^2-c\Rightarrow 3=1-c\Rightarrow c=-2, 故選\bbox[red,2pt]{(A)}$$
解：$$f'\left( 2 \right) =\lim _{ x\to 2 }{ \frac { f\left( x \right) -f\left( 2 \right) }{ x-2 } } =\lim _{ h\to 0 }{ \frac { f\left( h+2 \right) -f\left( 2 \right) }{ h } } =\lim _{ h\to 0 }{ \frac { \sqrt { 3\left( h+2 \right) -2 } -2 }{ h } } ,故選\bbox[red,2pt]{(B)}$$
解：$$y=f\left( x \right) \Leftrightarrow x=f^{ -1 }\left( y \right) \\ 4=f\left( x \right) =x^{ 3 }+x+2\Rightarrow x=1\Rightarrow f^{ -1 }\left( 4 \right) =1\\ \frac { d }{ dx } f^{ -1 }\left( x \right) =\frac { 1 }{ f'\left( f^{ -1 }\left( x \right) \right) } =\frac { 1 }{ f'\left( 1 \right) } =\frac { 1 }{ 3\cdot 1^{ 2 }+1 } =\frac { 1 }{ 4 } ,故選\bbox[red,2pt]{(D)}$$
解：$$f\left( x \right) =\ln { \left( \frac { { e }^{ x } }{ 2+{ e }^{ x } } \right) } =\ln { { e }^{ x } } -\ln { \left( 2+{ e }^{ x } \right) } =x-\ln { \left( 2+{ e }^{ x } \right) } \Rightarrow f'\left( x \right) =1-\frac { { e }^{ x } }{ 2+{ e }^{ x } } \\ \Rightarrow f'\left( 0 \right) =1-\frac { 1 }{ 2+1 } =\frac { 2 }{ 3 } ,故選\bbox[red,2pt]{(B)}$$
解：$$\begin{cases} x=t^{ 2 }+t+1 \\ y=\sqrt { t+3 } \end{cases}\Rightarrow \begin{cases} \frac { dx }{ dt } =t^{ 2 }+t+1 \\ \frac { dy }{ dt } =\frac { 1 }{ 2\sqrt { t+3 } } \end{cases}\Rightarrow \begin{cases} \left. \frac { dx }{ dt } \right| _{ t=1 }=1+1+1=3 \\ \left. \frac { dy }{ dt } \right| _{ t=1 }=\frac { 1 }{ 2\sqrt { 4 } } =\frac { 1 }{ 4 } \end{cases}\Rightarrow \left. \frac { dy }{ dt } \right| _{ t=1 }=\frac { \frac { 1 }{ 4 } }{ 3 } =\frac { 1 }{ 12 } \\故選\bbox[red,2pt]{(D)}$$
解：$$u=2x+3\Rightarrow \begin{cases} x=\frac { u-3 }{ 2 } \\ du=2dx \end{cases}\Rightarrow \int { \frac { x }{ \sqrt { 2x+3 } } } dx=\int { \frac { \frac { u-3 }{ 2 } }{ \sqrt { u } } \cdot \frac { 1 }{ 2 } } du=\frac { 1 }{ 4 } \int { \left( u-3 \right) u^{ -1/2 } } du\\ =\frac { 1 }{ 4 } \int { \left( u^{ 1/2 }-3u^{ -1/2 } \right) } du, 故選\bbox[red,2pt]{(A)}$$
解：$$\begin{cases} u=\ln { x } \\ dv=xdx \end{cases}\Rightarrow \begin{cases} du=\frac { 1 }{ x } dx \\ v=\frac { 1 }{ 2 } x^{ 2 } \end{cases}\Rightarrow \int { x\ln { x } } dx=\frac { 1 }{ 2 } x^{ 2 }\ln { x } -\frac { 1 }{ 2 } \int { x } dx=\frac { 1 }{ 2 } x^{ 2 }\ln { x } -\frac { 1 }{ 4 } x^{ 2 }+C \\故選\bbox[red,2pt]{(D)}$$
解：$$\left( \ln { \left| \sec { x } \right| } +C \right) '=\frac { 1 }{ \sec { x } } \cdot \frac { \sin { x } }{ \cos ^{ 2 }{ x } } =\frac { \sin { x } }{ \cos { x } } =\frac { f\left( x \right) }{ \cos { x } } \Rightarrow f\left( x \right) =\sin { x } ,故選\bbox[red,2pt]{(B)}$$
解：$$\begin{cases} u=\tan ^{ -1 }{ x } \\ dv=dx \end{cases}\Rightarrow \begin{cases} du=\frac { 1 }{ 1+x^{ 2 } } dx \\ v=x \end{cases}\Rightarrow \int { \tan ^{ -1 }{ x } } dx=x\tan ^{ -1 }{ x } -\int { \frac { x }{ 1+x^{ 2 } } } dx\\ =x\tan ^{ -1 }{ x } -\frac { 1 }{ 2 } \ln { \left( 1+x^{ 2 } \right) } +C,故選\bbox[red,2pt]{(C)}$$
解：$$\int { y } dx=\int _{ 0 }^{ 1 }{ 2x } dx,故選\bbox[red,2pt]{(D)}$$
解：
由於\(x\)介於-1與1之間，且\(\sqrt{1-x^2}\ge 0\)，因此只有上半圓面積，故選\(\bbox[red,2pt]{(C)}\)
解：$$\int _{ 2 }^{ e }{ \frac { 1 }{ x\ln { x } } } dx=\left. \left[ \ln { \left( \ln { x } \right) } \right] \right| ^{ e }_{ 2 }=\ln { \left( \ln { e } \right) } -\ln { \left( \ln { 2 } \right) } =\ln { \left( 1 \right) } -\ln { \left( \ln { 2 } \right) } =-\ln { \left( \ln { 2 } \right) } ,故選\bbox[red,2pt]{(D)}$$
解：
令\(f(x)=\frac{\tan{x}}{x^2+x^4}\Rightarrow f(-x)=-f(x)\)，該圖形對稱原點，因此\(x=-1\)至\(x=1\)間的面積為0，故選\(\bbox[red,2pt]{(A)}\)
解：三次函數且首項係數為正值，其圖形為左下右上形，遞減區間在極大值與極小值之間；$$f\left( x \right) =x^{ 3 }+3x^{ 2 }+2\Rightarrow f'\left( x \right) =3x^{ 2 }+6x\Rightarrow f''\left( x \right) =6x+6\\ f'\left( x \right) =0\Rightarrow 3x\left( x+2 \right) =0\Rightarrow x=0,-2有極值\\ \begin{cases} f''\left( 0 \right) =6>0 \\ f''\left( -2 \right) =-6<0 \end{cases}\Rightarrow f\left( 0 \right) 為極小值,f\left( -2 \right) 為極大值\Rightarrow f\left( x \right) 在區間\left( -2,0 \right) 為遞減\\ \Rightarrow 故選\bbox[red,2pt]{(B)}$$
解：$$f\left( x \right) =x^{ 4 }-4x^{ 3 }+18\Rightarrow f'\left( x \right) =4x^{ 3 }-12x^{ 2 }\Rightarrow f''\left( x \right) =12x^{ 2 }-24x\\ f''\left( x \right) =0\Rightarrow 12x^{ 2 }-24x=0\Rightarrow 12x\left( x-2 \right) =0\Rightarrow x=0,2\\ \Rightarrow \begin{cases} f\left( 0 \right) =18 \\ f\left( 2 \right) =2 \end{cases}\Rightarrow \left( 0,18 \right) ,\left( 2,2 \right) 為反曲點\Rightarrow 故選\bbox[red,2pt]{(C)}$$
解：利用羅必達原理，即$$\lim _{ x\to 0 }{ \left( \frac { 1 }{ x } -\frac { 1 }{ e^{ x }-1 } \right) } =\lim _{ x\to 0 }{ \left( \frac { e^{ x }-x-1 }{ xe^{ x }-x } \right) } =\lim _{ x\to 0 }{ \left( \frac { e^{ x }-1 }{ xe^{ x }+e^{ x }-1 } \right) } =\lim _{ x\to 0 }{ \left( \frac { e^{ x } }{ xe^{ x }+2e^{ x } } \right) } =\frac { 1 }{ 2 }\\ \Rightarrow 故選\bbox[red,2pt]{(C)}$$
解：$$\sin { x } =\sum _{ n=1 }^{ \infty }{ \frac { { \left( -1 \right) }^{ n-1 } }{ \left( 2n-1 \right) ! } x^{ 2n-1 } } =x-\frac { 1 }{ 3! } x^{ 3 }+\frac { 1 }{ 5! } x^{ 5 }+\cdots \\ \Rightarrow \sin { x^{ 2 } } =x^{ 2 }-\frac { 1 }{ 3! } x^{ 6 }+\frac { 1 }{ 5! } x^{ 10 }+\cdots \Rightarrow a_{ 2 }=1,a_{ 3 }=a_{ 5 }=0,a_{ 6 }=-\frac { 1 }{ 6 } \Rightarrow 故選\bbox[red,2pt]{(D)}$$
解：$$\sum _{ n=1 }^{ \infty }{ \frac { 2 }{ \left( 2n-1 \right) \left( 2n+1 \right) } } =\sum _{ n=1 }^{ \infty }{ \left( \frac { 1 }{ 2n-1 } -\frac { 1 }{ 2n+1 } \right) } =1-\frac { 1 }{ 3 } +\frac { 1 }{ 3 } -\frac { 1 }{ 5 } +\cdots =1\Rightarrow 故選\bbox[red,2pt]{(A)}$$
解：$$\int _{ 0 }^{ 1 }{ \sqrt { 1+{ \left( \frac { dy }{ dx } \right) }^{ 2 } } } dx=\int _{ 0 }^{ 1 }{ \sqrt { 1+{ \left( 2x \right) }^{ 2 } } } dx=\int _{ 0 }^{ 1 }{ \sqrt { 1+4x^{ 2 } } } dx\Rightarrow 故選\bbox[red,2pt]{(B)}$$
解：$$f'\left( 0 \right) =\lim _{ h\to 0 }{ \frac { f\left( h \right) -f\left( 0 \right) }{ h } } =\lim _{ h\to 0 }{ \frac { h^{ 2 }\sin { \frac { 1 }{ h } } -0 }{ h } } =\lim _{ h\to 0 }{ \left( h\sin { \frac { 1 }{ h } } \right) } =0 \Rightarrow 故選\bbox[red,2pt]{(A)}$$
解：
假設圓柱體的高度\(h=2a\)，底面圓半徑為\(r\)，由於該圓柱體外接一球，球半徑為1，即\(a^2+r^2=1\Rightarrow r=\sqrt{1-a^2}\)；因此圓柱體體積為：$$f\left( a \right) =r^{ 2 }\pi \times 2a=\left( 1-a^{ 2 } \right) 2a\pi =\left( 2a-2a^{ 3 } \right) \pi \Rightarrow f'\left( a \right) =0\Rightarrow 2-6a^{ 2 }=0\\ \Rightarrow a=\sqrt { \frac { 1 }{ 3 } } 有極大值f\left( \sqrt { \frac { 1 }{ 3 } } \right) =\left( 1-\frac { 1 }{ 3 } \right) \times 2\times \sqrt { \frac { 1 }{ 3 } } \times \pi \\ =\frac { 4\pi }{ 3 } \times \frac { \sqrt { 3 } }{ 3 } =\frac { 4\sqrt { 3 } \pi }{ 9 } \Rightarrow 故選\bbox[red,2pt]{(B)}$$
解：$$\begin{cases} x=r\cos { \theta } \\ y=r\sin { \theta } \end{cases}\Rightarrow \begin{cases} r=\sqrt { x^{ 2 }+y^{ 2 } } \\ \sin { \theta } =\frac { y }{ \sqrt { x^{ 2 }+y^{ 2 } } } \end{cases}\Rightarrow r=2\sin { \theta } \Rightarrow \sqrt { x^{ 2 }+y^{ 2 } } =\frac { 2y }{ \sqrt { x^{ 2 }+y^{ 2 } } } \\ \Rightarrow x^{ 2 }+y^{ 2 }=2y\Rightarrow x^{ 2 }+{ \left( y-1 \right) }^{ 2 }=1\Rightarrow 半徑為1的圓\Rightarrow 面積=\pi \Rightarrow 故選\bbox[red,2pt]{(A)}$$
解：
任何數的0次方皆為1，0的0次方也是1，故選\(\bbox[red,2pt]{(B)}\)
解題僅供參考
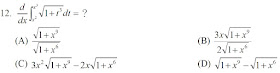
作者已經移除這則留言。
回覆刪除老師好，請問第二題的定義域，在根號裡的5-x為什麼不需討論?
回覆刪除5-x 開3次方不是2次方，所以無論5-x是正是負都是可以的!!
刪除老師好:請問第九題為什麼不是用1次微分=0 求臨界點?
回覆刪除1次微分=0 是用來求極值的，不是求臨界點!
刪除我是參考這個https://www.youtube.com/watch?v=JKo04QSwYhU
刪除與微積分書籍