107年建中教甄-數學詳解

臺北市立建國高級中學 107 學年度第一次正式教師甄選

一、填充題： (每題 7 分，共 70 分)

解答：$$\cases{A=\{e^{k\pi i/6},k=1-12\} \\B=\{e^{t\pi i/8},t=1-16\}} \Rightarrow C=\{e^{s\pi i/48},s= (kt \mod 48)+1\} \Rightarrow \#(C)=\bbox[red, 2pt]{48}$$

解答：$$先求A=\sum_{k=1}^n {k\over 2^k} ={1\over 2} +{2\over 2^2}   +\cdots +{n\over 2^n} \Rightarrow {1\over 2}A={1\over 2^2} +{2\over 2^3}  +\cdots +{n-1\over 2^n}+{n\over 2^{n+1}}\\ A-{1\over 2}A={1\over 2}+ {1\over 2^2}+ \cdots +{1\over 2^n}-{n\over 2^{n+1}} \Rightarrow {1\over 2}A={1/2-1/2^{n+1} \over 1-1/2} -{n\over 2^{n+1}}=1-{1\over 2^n}-{n\over 2^{n+1}}\\ \Rightarrow A=2-{n+2\over 2^n}\\ 現在B=\sum_{k=1}^n {k^2\over 2^k} ={1\over 2} +{2^2\over 2^2}   +\cdots +{n^2\over 2^n} \Rightarrow {1\over 2}B= {1\over 2^2} +{2^2\over 2^3}   +\cdots + {(n-1)^2\over 2^{n}}+{n^2\over 2^{n+1}} \\ \Rightarrow B-{1\over 2}B={1\over 2} +{3\over 2^2}   +\cdots + {2n-1\over 2^{n}}-{n^2\over 2^{n+1}} =\sum_{k=1}^n {2k-1\over 2^k}-{n^2\over 2^{n+1}} \\=2\sum_{k=1}^n {k\over 2^k}-\sum_{k=1}^n{1\over 2^k}-{n^2\over 2^{n+1}}=2A-\left(1-{1\over 2^n} \right)-{n^2\over 2^{n+1}} =2\left(2-{n+2\over 2^n}\right)-1+{1\over 2^n}-{n^2\over 2^{n+1}}\\ =3-{n+2\over 2^{n-1}} +{1\over 2^n}-{n^2\over 2^{n+1}} \Rightarrow B=6-{n+2\over 2^{n-2}}+{1\over 2^{n-1}}- {n^2\over 2^n} =\bbox[red, 2pt]{6-{n^2+4n+6\over 2^n}}$$

解答：$$a^4+18^2=(a^2)^2+18^2= (a^2+18)^2-36a^2 =(a^2+18)^2-(6a)^2 =(a^2+6a+18)(a^2-6a+18)\\ =((a+3)^2+9)((a-3)^2+9)\\ \Rightarrow 分子=(4^2+9)(2^2+9)(14^2+9)(8^2+9)(26^2+9)(20^2+9)(38^2+9)(32^2+9)(50^2+9)(44^2+9) \\，分母= (8^2+9)(2^2+9) (10^2+9)(4^2+9)(20^2+9)(14^2+9)(32^2+9)(26^2+9)(44^2+9)(38^2+9)\\ \Rightarrow {分子\over 分母}={50^2+9 \over 10^2+9 } = \bbox[red,2pt]{2509\over 109}$$

解答：$$沒有什麼好方法，只能先考慮f:B\to B，再將A\to \{5,6\}及\{5,6\}\to A或反之\\，一個個加入計算，共4!\times 16+8\times 60=\bbox[red, 2pt]{864}$$

解答：$$令\cases{f(x,y)=x^3+y^3+{9\over 2}x +{9\over 2}y\\ g(x,y)=x^2+y^2-x-y}及f=\lambda g ，則 \cases{f_x=\lambda g_x\\ f_y=\lambda g_y}\Rightarrow \cases{3x^2+{9\over 2}=\lambda (2x-1) \cdots(1)\\ 3y^2+{9\over 2}=\lambda (2y-1) \cdots(2)}\\ {(1)\over (2)} \Rightarrow {3x^2+9/2\over 3y^2+9/2} ={2x-1\over 2y-1} \Rightarrow 6x^2y-3x^2+9y = 6xy^2-3y^2+9x \\\Rightarrow 2xy(x-y)-(x^2-y^2)-3(x-y)=0 \Rightarrow (x-y)(2xy-x-y-3)=0 \Rightarrow x=y\\ 將x=y代入g(x,y)=0 \Rightarrow 2x^2-2x=0 \Rightarrow x=1 \Rightarrow f(1,1)=2+9=\bbox[red,2pt]{11}$$

解答：

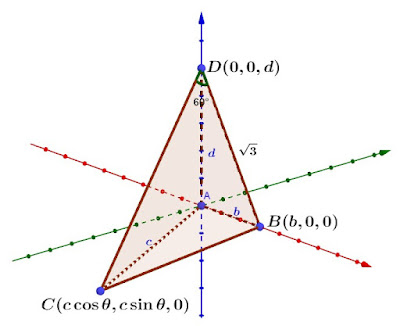
$$假設\cases{A(0,0,0)\\ B在x軸上\\ C在xy平面上\\ \overline{AB}=b\\ \overline{AC}=c\\ \overline{AD}=d} \Rightarrow \cases{B(b,0,0)\\ C(c\cos \theta,c\sin \theta,0)\\ D(0,0,d)} \Rightarrow \cases{\overrightarrow{DB}=(b,0,-d)\\ \overrightarrow{DC}=(c\cos\theta,c\sin \theta,-d)} \\ \Rightarrow \cases{平面BCD法向量\vec u=\overrightarrow{DB} \times \overrightarrow{DC}= (cd\sin \theta,bd-cd\cos \theta,bc\sin \theta) \\平面ABD: y=0 \Rightarrow 法向量\vec v=(0,1,0)}\\ 由於ABD\bot BCD \Rightarrow \vec u\cdot \vec v=0 \Rightarrow bd=cd\cos \theta \Rightarrow b=c\cos\theta \Rightarrow \cos \theta ={b\over c} \Rightarrow \angle ABC=90^\circ \\ \Rightarrow \angle DBC=90^\circ \Rightarrow \cases{\overline{CD}= 2\times \overline{BD}=2\sqrt 3\\ \overline{BC}=\sqrt 3\times \overline{BD}=3} \Rightarrow \cases{\triangle ABD=bd/2\\ \triangle ACD=cd/2 \\ \triangle BCD=\overline{CD}\cdot \overline{BD}\sin 60^\circ /2=3\sqrt 3/2}\\ \Rightarrow \triangle ABD^2 +\triangle ACD^2 +\triangle BCD^2 ={1\over 4}(b^2d^2+c^2d^2+27)=10 \Rightarrow d^2(b^2+ c^2)=13 \\ \Rightarrow (3-b^2)(b^2+b^2+3^2)=13 \Rightarrow 2b^4+3b^2-14=0 \Rightarrow (b^2-2)(2b^2+7)=0\\ \Rightarrow b=\sqrt 2 \Rightarrow \sin ADB ={b\over \sqrt 3} ={\sqrt 2\over \sqrt 3} =\bbox[red,2pt]{\sqrt 6\over 3}$$

解答：

$$令\cases{E(1,0)\\ P為\overline{AC}中點\\ Q為\overline{BD}中點\\ \overline{OP}=a\\ \overline{OQ}=b}，則\cases{\overline{OP} \bot \overline{AC}\\ \overline{OQ} \bot \overline{BD} \\ a^2+b^2=1}；因此\cases{\overline{AP}=\sqrt{2^2-a^2} \\ \overline{BQ}= \sqrt{2^2-b^2}} \\ \Rightarrow ABCD面積={1\over 2}\times \overline{AC}\times \overline{BD} ={1\over 2}\times 2\overline{AP}\times 2\overline{BQ}\\ =2\times \sqrt{4-a^2} \times \sqrt{4-b^2} \le (4-a^2)+(4-b^2) =8-1=7 \Rightarrow 面積最大值為\bbox[red, 2pt]{7}$$

解答：$$令\cases{A(0,0,0)\\ C(9,0,0)\\ B(a,b,0)}，則\cases{\overline{AB}=5\\ \overline{BC}=8} \Rightarrow \cases{a^2+b^2=25\\ (a-9)^2+b^2 =64} \Rightarrow -18a+81+25=64 \Rightarrow a={7\over 3} \\ \Rightarrow ({7\over 3})^2+b^2 =25 \Rightarrow b^2={176\over 9}，取b={4\over 3}\sqrt{11} \Rightarrow B({7\over 3}, {4\over 3}\sqrt{11},0)\\ 再令D(\alpha,\beta,\gamma)，則\cases{\overline{AD}= 11 \\ \overline{BD}=12 \\\overline{CD}=10} \Rightarrow \cases{\alpha^2 +\beta^2+\gamma^2=121 \cdots(1)\\ (\alpha-{7\over 3})^2 +(\beta-{4\over 3}\sqrt{11})^2 +\gamma^2=144 \cdots(2) \\ (\alpha-9)^2 +\beta^2+\gamma^2 =100 \cdots(3)}\\ 將(1)代入(3) \Rightarrow -18\alpha+81+121=100 \Rightarrow \alpha={17\over 3}代入(1)及(2) \Rightarrow \cases{\beta^2+\gamma^2 = {800\over 9}\\ (\beta-{4\over 3}\sqrt{11})^2 +\gamma^2= {1196\over 9}} \\ \Rightarrow -{8\over 3}\sqrt{11}\beta ={220\over 9} \Rightarrow \beta=-{5\over 6}\sqrt{11} \Rightarrow \gamma^2={800\over 9} -{275\over 36} ={325\over 4} ，取\gamma ={5\over 2}\sqrt{13} \\\Rightarrow D({17\over 3},-{5\over 6}\sqrt{11}, {5\over 2}\sqrt{13}) \Rightarrow \cases{\overrightarrow{DA}= (-{17\over 3},{5\over 6}\sqrt{11}, -{5\over 2}\sqrt{13}) \\ \overrightarrow{DC}= ({10\over 3}, {5\over 6}\sqrt{11}, -{5\over 2}\sqrt{13})} \\\Rightarrow \vec u= \overrightarrow{DA} \times \overrightarrow{DC}= (0,-{45\over 2}\sqrt{13},-{15\over 2}\sqrt{11})；\\而平面ABC的法向量為\vec v=(0,0,1)，因此\cos \theta ={\vec u\cdot \vec v\over |\vec u||\vec v|} ={-{15\over 2}\sqrt{11}\over 60\sqrt 2} = \bbox[red,2pt]{-{\sqrt{22}\over 16}}$$

解答：$$6+{1\over n+1}\lt \sqrt[3]{220} \lt 6+{1\over n} \Rightarrow {1\over n+1}\lt \sqrt[3]{220}-6 \lt {1\over n} \Rightarrow n \lt {1\over \sqrt[3]{220}-6 }\lt n+1 \\  {1\over \sqrt[3]{220}-6 }= {3\sqrt{220^2}+6 \sqrt[3]{220}+6^2 \over (\sqrt[3] {220})^3-6^3)} ={\sqrt[3]{220^2}+ 6\sqrt[3]{220}+36 \over 4} \\\Rightarrow {6^2+6\cdot 6+36\over 4} \lt {1\over \sqrt[3]{220}-6 } \lt {6.1^2+6\cdot 6.1 +36\over 4}\left(\because \cases{6^3=216\\ 6.1^3 \approx227} \Rightarrow 6\lt \sqrt[3]{220} \lt 6.1\right)\\ \Rightarrow {108\over 4}\lt {1\over \sqrt[3]{220}-6 } \lt {109.81\over 4} \Rightarrow 27\lt {1\over \sqrt[3]{220}-6 } \lt 27.4525 \Rightarrow n=\bbox[red,2pt]{27}$$

解答：$${x\over 61}=0.d_1d_2d_3\cdots，因此\cases{d_{37}=2 \Rightarrow 10^{36}x\equiv 13,14,15,16,17,18 \;(\mod 61) \cdots(1) \\d_{65}=3 \Rightarrow 10^{64}x \equiv 19,20,21,22,23,24 \;(\mod 61) \cdots(2)} \\ 而10000= 164\times 61-4 \Rightarrow 10^4 \equiv -4 \mod 61 \Rightarrow 10^{28} \equiv 25 \mod 61\\，因此\cases{若10^{36}x =13\mod 61 \Rightarrow 10^{28}\cdot 10^{36}x= (13\times 25) \mod 61 \Rightarrow 10^{64}x = 20 \mod 61 \\若10^{36}x =14\mod 61 \Rightarrow 10^{28}\cdot 10^{36}x= (14\times 25) \mod 61 \Rightarrow 10^{64}x = 45 \mod 61\\ 若10^{36}x =15\mod 61 \Rightarrow 10^{28}\cdot 10^{36}x= (15\times 25) \mod 61 \Rightarrow 10^{64}x = 9 \mod 61\\ 若10^{36}x =16\mod 61 \Rightarrow 10^{28}\cdot 10^{36}x= (16\times 25) \mod 61 \Rightarrow 10^{64}x = 34 \mod 61 \\ 若10^{36}x =17\mod 61 \Rightarrow 10^{28}\cdot 10^{36}x= (17\times 25) \mod 61 \Rightarrow 10^{64}x = 59 \mod 61\\ 若10^{36}x =18\mod 61 \Rightarrow 10^{28}\cdot 10^{36}x= (18\times 25) \mod 61 \Rightarrow 10^{64}x = 23 \mod 61}\\ 有兩組解符合(1)及(2)，即\cases{10^{36}x \equiv 13 \mod 61\\ 10^{64}x \equiv 20 \mod 61} 及\cases{10^{36}x \equiv 18 \mod 61\\ 10^{64}x \equiv 23 \mod 61}\\ 由於10^{36} \equiv 34 \mod 61 \Rightarrow \cases{\cases{10^{36}x \equiv 13 \mod 61\\ 10^{36} \equiv 34 \mod 61} \Rightarrow x \equiv 56 \mod 61 \\\cases{10^{36}x \equiv 18 \mod 61\\ 10^{36} \equiv 34 \mod 61} \Rightarrow x \equiv 40 \mod 61 }\\ 又10^{35}\equiv 40 \mod 61 \Rightarrow \cases{x \equiv 56 \mod 61 \Rightarrow 10^{35}x \equiv 44 \mod 61 \Rightarrow d_{36}=7 \\ x \equiv 40 \mod 61 \Rightarrow 10^{35}x \equiv 14 \mod 61 \Rightarrow d_{36}=2}\\ 因此(x,d_{36})= \bbox[red,2pt]{(56,7),(40,2)}\\ 學校公佈的答案只有\bbox[blue,2pt]{(56,7)}，經電腦計算，(40,2)也合乎要求!$$

===== END ====

學校未公告計算題題目，解題僅供參考，其他教甄試題及詳解