103年初等考試-統計學大意詳解

103 年公務人員初等考試

等 別：初等考試
類 科：統計
科 目：統計學大意

解答：$$溫度可比較高低(加減運算)，不能計算比率，故選\bbox[red,2pt]{(C)}$$

解答：$$不同單位，其平均數不同，因此需採用CV而非VAR，故選\bbox[red,2pt]{(D)}$$

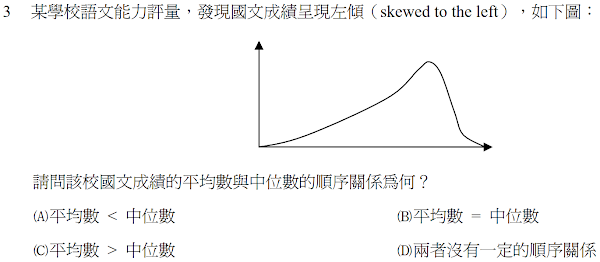
解答：$$圖形為左偏，因此中位數\gt 平均數，故選\bbox[red,2pt]{(A)}$$

解答：$$P(1,1)+P(1,2)+ P(2,1) + P(1,3)+ P(3,1)+ P(2,2) \\=({1\over 4})^2+{1\over 4}\cdot {1\over 8}+{1\over 8}\cdot {1\over 4}+{1\over 4}\cdot {1\over 8} +{1\over 8}\cdot {1\over 4}+ ({1\over 8})^2 \\ ={1\over 16}+ {4\over 32} +{1\over 64} ={ 13\over 64}，故選\bbox[red,2pt]{(C)}$$

解答：$${檢驗為陰性且無患病\over 檢驗為陰性且患病+檢驗為陰性且無患病} ={95\% \times 8599\%\over 5\% \times 12\% + 95\%\times 85\%} = 99.262\%，故選\bbox[red,2pt]{(D)}$$

解答：

$$\cases{A+D+F+G = 220\\ B+D+E +G=180\\ C+E+F+G= 150\\ D+G = 150\\ F+G=80\\ E+G=100\\ A+B+C+D +E+F+G=300} \Rightarrow \cases{A+F=70\\ B+D=80\\ C+E=70} \Rightarrow A+B+C+D+E+F =220\\ \Rightarrow G=300-220=80 \Rightarrow 機率={80\over 300}={4\over 15}，故選\bbox[red,2pt]{(D)}$$

解答：$$P(A^c\cap B^c) = 1-P(A\cup B)=1-(P(A)+P(B)- P(A\cap B))= 1-(0.3+0.4-0.3\cdot 0.4)\\ =0.42，故選\bbox[red,2pt]{(A)}$$

解答：$$\cases{P(A\mid B)=P(A\cap B)/P(B)=0.25 \\ P(B\mid A)=P(A\cap B)/P(A) =0.5} \Rightarrow P(A \cap B)=0.25P(B)= 0.5P(A) \\ \Rightarrow P(A)= 0.25P(B)/0.5 = 0.25\times 0.3\div 0.5=0.15，故選\bbox[red,2pt]{(D)}$$

解答：$$X\sim B(n=20,p=180/300) \Rightarrow Var(X)=np(1-p)=20\times {3\over 5}\times{2\over 5}=4.8\\由於有限母體，需校正，即4.8\times {N-n\over N-1}=4.8\times {280\over 299}=4.495，故選\bbox[red,2pt]{(C)}$$

解答：$$當N\to \infty時，超幾何趨近二項分配，故選\bbox[red,2pt]{(A)}$$

解答：$$指數分配，其E(Y)=1/43，故選\bbox[red,2pt]{(D)}$$

解答：$$\cases{E(X)=\lambda\\ E(Y)=1/\lambda} \Rightarrow E(X)E(Y)=1，故選\bbox[red,2pt]{(D)}$$

解答：$$z分配，故選\bbox[red,2pt]{(C)}$$

解答：$$P(X\ge 2)=1-P(X=0)-P(X=1)= 1-0.6^{10}-C^{10}_1\cdot 0.6^9\cdot 0.4 =0.9536，故選\bbox[red,2pt]{(D)}$$

解答：$$\cases{男生上網比例p_1=310/560\\ 女生上網比例p_2=300/640} \Rightarrow \sqrt{{p_1(1-p_1)\over 560} +{p_2(1-p_2)\over 640}} =0.02882，故選\bbox[red,2pt]{(B)}$$

解答：$$E(\hat \theta-\theta)=E(\hat \theta)-\theta，故選\bbox[red,2pt]{(C)}$$

解答：$$\cases{母體的一階動差=E(X)={0+\theta\over 2} ={\theta\over 2}\\ 樣本的一階動差={1\over n}(X_1+\cdots +X_n)=\bar X}\\ \Rightarrow 兩者相等，即{\theta \over 2}=\bar X \Rightarrow \theta =2\bar X，故選\bbox[red,2pt]{(C)}$$

解答：$$n\ge z_{\alpha/2}\cdot {p(1-p)\over E^2} =1.96^2 \times {0.3\times 0.7\over 0.03^2} =896.37 \Rightarrow n=897，故選\bbox[red,2pt]{(B)}$$

解答：$$E({\sum X_i^2\over n}) ={1\over n}E(X_1^2 +X_2^2 +\cdots +X_n^2) ={1\over n}\left( n(\sigma^2 +\mu^2)\right) =\sigma^2 +\mu^2 \\ \Rightarrow {\sum X_i^2\over n} 是\sigma^2 +\mu^2的不偏估計量\\ E({\sum (X_i-\bar X)^2\over n}) ={1\over n} E(\sum X_i^2-n(\bar X)^2) ={1\over n}\left( \sum E(X^2)-nE((\bar X)^2)\right)\\ ={1\over n}\left( n(\sigma^2+\mu^2) -n\left({\sigma^2\over n}+\mu^2 \right)\right) ={n-1\over n} \sigma^2  \ne \sigma^2\\ \Rightarrow {\sum (X_i-\bar X)^2\over n} 不是\sigma^2的不偏估計量\\，故選\bbox[red,2pt]{(B)}$$

解答：$$z_{0.025}/z_{0.05} =1.96/1.65=1.1879，故選\bbox[red,2pt]{(C)}$$

解答：$$p值\lt \alpha，則拒絕H_0，故選\bbox[red,2pt]{(B)}$$

解答：$$樣本數增加，則誤差減少，故選\bbox[red,2pt]{(B)}$$

解答：$$\cases{H_0:p\le 0.3\\ H_1:p\gt 0.3}，若能拒絕H_0則證明p\gt 30\%是正確的，因此對立假設為p\gt 0.3，故選\bbox[red,2pt]{(D)}$$

解答：$$\alpha越大，拒絕H_0機會越大，接受H_0機率越小，因此\beta變小，故選\bbox[red,2pt]{(B)}$$

解答：$$0.006 小於 1\%、5\%，也小於1\%/2、5\%/2；且0.006 \gt 0.1\%，故選\bbox[red,2pt]{(B)}$$

解答：$${600-\bar x\over \sqrt{50/20}} \gt z_{0.05} =1.645 \Rightarrow \bar x\lt 600-1.645\times \sqrt{2.5}=597.399，故選\bbox[red,2pt]{(D)}$$

解答：$$各組相同，即各組平均數相同，故選\bbox[red,2pt]{(D)}$$

解答：$$ANOVA檢定統計量為F，故選\bbox[red,2pt]{(B)}$$

解答：$$共k組，因此自由度為k-1，故選\bbox[red,2pt]{(B)}$$

解答：$$k個\alpha_i及1個\mu，共k+1個參數，故選\bbox[red,2pt]{(B)}$$

解答：$$相關係數r=1.5916\times {8.88\over 14.45} =0.97809，故選\bbox[red,2pt]{(D)}$$

解答：$$E\hat \theta_1 = E\hat\theta_2 = \theta \Rightarrow \hat \theta_1與\hat \theta_2 為不偏估計量，故選\bbox[red,2pt]{(D)}$$

解答：$$(5-1)\times (8-1)=28，故選\bbox[red,2pt]{(C)}$$

解答：$$每個細格需\ge 5，故選\bbox[red,2pt]{(C)}$$

解答：$$10組\Rightarrow 自由度=10-1=9，再加上適合度檢定，因此9-1=8，故選\bbox[red,2pt]{(B)}$$

解答：$$\cases{總反對人數=55+30+25 = 110，占比為{110\over 200}\\ 中部總人數=20+30=50} \Rightarrow 中部反對預期人數=50\times {110\over 200} =27.5\\，故選\bbox[red,2pt]{(A)}$$

解答：$$期望值:\begin{array}{|c|c|c|c|}\hline  & 北部 & 中部 & 南部\\\hline 贊成& 40.5 & 22.5 & 27 \\\hline 反對& 49.5 & 27.5 & 33\\\hline \end{array} \\ \Rightarrow 檢定統計量 = {(35-40.5)^2 \over 40.5} +{(20-22.5)^2 \over 22.5} +{(35-27)^2 \over 27} +{55-49.5)^2\over 49.5} +{(30-27.5)^2 \over 27.5}\\\qquad +{(25-33)^2\over 33}=6.1728，故選\bbox[red,2pt]{(D)}$$

解答：$$另一個是隨機，不是規則變動，故選\bbox[red,2pt]{(D)}$$

解答：$$評審有三位，自由度為3-1=2，故選\bbox[red,2pt]{(B)}$$

解答：$$\cases{F(10)=48.536\\ D(10)=48.7} \Rightarrow F(11)=F(10)+\alpha (D(10)-F(10)) \\ \Rightarrow F(11)=48.536+0.4(48.7-48.536) = 48.6016，故選\bbox[red,2pt]{(A)}$$

=================== END ===========================

解題僅供參考，其他國考試題及詳解