國立臺南女中108學年度第 4 次教師甄選
(每題 5 分 ,答案請化為最簡分數或最簡根式 )
解答:$$\cases{A(0,3,-2)\\ B(0,9,-10)\\ P(3,3,2)} \Rightarrow \cases{\overline{AB}=10 \\ \overline{AP}=5} \Rightarrow \overline{PQ}: \overline{QB} = \overline{AP} : \overline{AB}=5:10 = 1:2 \\ \Rightarrow Q={1\over 3}B +{2\over 3}P = (2,5,-2) \Rightarrow 平面E的法向量=\overrightarrow{AQ} =(2,2,0) \\\Rightarrow E:2(x-0)+2(y-3)+0(z+2)=0 \Rightarrow \bbox[red, 2pt]{x+y=3}$$
解答:$$d= A至平面CDE的距離 = \frac{3+2+6-5}{\sqrt{1^2+2^2+2^2}} =2 \Rightarrow 稜長\overline{AD} = d\times \sqrt 2=\bbox[red, 2pt]{2\sqrt 2}$$
解答:
解答:
$$令\cases{S_1:\cases{甲袋:2紅1白\\ 乙袋:1白} \\ S_2:\cases{甲袋:1紅2白\\ 乙袋:1紅}},則\cases{P(S_1\to S_1)=1/3\\ P(S_1\to S_2)=2/3\\ P(S_2\to S_1)= 2/3 \\ P(S_2\to S_2) = 1/3};\\因此玩3局還是在S_1的情形及其機率為\cases{P(S_1\to S_1\to S_1 \to S_1) = 1/27\\ P(S_1\to S_1\to S_2\to S_1)=4/27\\ P(S_1\to S_2 \to S_1\to S_1)=4/27\\ P(S_1\to S_2 \to S_2\to S_1)= 4/27}\\ 因此機率為{1+4+4+4 \over 27 } =\bbox[red, 2pt]{13\over 27}$$
$$令C、D中點為坐標原點O(0,0,0),則\cases{C(-3,0,0)\\ D(3,0,0)\\ B(0,\sqrt 7,0)\\ A(0,a,b)};\\因此\cases{\overline{AB}=5\\ \overline{AD}=4} \Rightarrow \cases{(a-\sqrt 7)^2+b^2= 5^2 \cdots(1)\\ 3^2 +a^2+b^2 = 16 \cdots(2)};\\由(2)可得a^2+b^2 =7 代入(1) \Rightarrow 7-2\sqrt 7a+7=25 \Rightarrow a=-{11\over 2\sqrt 7} \Rightarrow b={5\sqrt 3\over 2\sqrt 7}\\ \Rightarrow \cases{\overrightarrow{AC} =(-3,{11\over 2\sqrt 7},-{5\sqrt 3\over 2\sqrt 7}) \\ \overrightarrow{AD}=(3,{11\over 2\sqrt 7},-{5\sqrt 3\over 2\sqrt 7}) \\ \overrightarrow{BC} =(-3,-\sqrt 7,0)\\ \overrightarrow{BD} =(3,-\sqrt 7, 0)} \Rightarrow \cases{\vec u= \overrightarrow{AC} \times \overrightarrow{AD} = (0,-{30\sqrt 3\over 2\sqrt 7}, -{66\over 2\sqrt 7})\\ \vec v= \overrightarrow{BC} \times \overrightarrow{BD} =(0,0,6\sqrt 7)}\\ \Rightarrow \cos \theta = {\vec u\cdot \vec v\over |\vec u||\vec v|} ={-198\over 252} =\bbox[red, 2pt]{-{11\over 14}}$$
解答:
解答:
$${(x-21)^2 \over 21} +{(y-100)^2\over 100} =2100 \Rightarrow {(x-21)^2 \over {1\over 100}} +{(y-100)^2\over {1\over 21}} =1 \Rightarrow \cases{a=1/\sqrt{21} \\ b=1/10} \Rightarrow c={\sqrt{79} \over 10\sqrt{21}}\\ \Rightarrow \cases{R_1-R_2=棕色區域\\ R_4-R_3= 藍色區域} \qquad \Rightarrow R_1-R_2+R_3-R_4= 矩形PQRS面積 \\= \overline{RS} \times \overline{PS} =42\times 200 =\bbox[red,2pt]{8400}$$
解答:$$A=\begin{bmatrix} 5& -2 \\ 8 & -3\end{bmatrix} \Rightarrow A^2= \begin{bmatrix} 9& -4 \\ 16 & -7\end{bmatrix} \Rightarrow A^4= \begin{bmatrix} 17& -8 \\ 32 & -15\end{bmatrix}\\ \Rightarrow A^6= \begin{bmatrix} 17& -8 \\ 32 & -15\end{bmatrix} \begin{bmatrix} 9& -4 \\ 16 & -7\end{bmatrix} = \bbox[red,2pt]{\begin{bmatrix} 25& -12 \\ 48 & -23\end{bmatrix}}$$
解答:
$$假設正方形BCDE邊長為2,中心點O為原點,則\cases{A(0,0,h)\\ B(-1,1,0)\\ C(1,1,0)\\ D(1,-1,0) \\ E(-1,-1,0)};\\由於坡度為{2\over 3} \Rightarrow h={2\over 3 } \Rightarrow A(0,0,{2\over 3}) \Rightarrow \cases{\overrightarrow{AD}= (1,-1,-{2\over 3})\\ \overrightarrow{AE}= (-1,-1,-{2\over 3})\\ \overrightarrow{AC}= (1,1,-{2\over 3}) }\\ \Rightarrow \cases{\vec u = \overrightarrow{AE} \times \overrightarrow{AD} =(0,-{4\over 3}, 2)\\\vec v = \overrightarrow{AD} \times \overrightarrow{AC} =({4\over 3},0,2)} \Rightarrow \cos \theta = {\vec u\cdot \vec v\over |\vec u||\vec v|} ={4\over 52/9} =\bbox[red, 2pt]{9\over 13}$$
解答:$$L_1:\cases{x+y=2\\ y+z=1} \equiv (2-t,t,1-t), t\in R \Rightarrow L_1方向向量\vec u=(-1,1,-1);\\ L_2:\cases{x=2\\ y-z=3} \equiv (2,s,s-3),s\in R \Rightarrow L_2方向向量\vec v=(0,1,1);\\因此\vec u \bot \vec v,且L_1,L_2無交點,即兩直線歪斜;\\ \cases{在L_1任找一點P(2,0,1)\\ 在L_2任找一點Q(2,0,-3) \\ \vec n=\vec u\times \vec v = (2,1,-1)} \Rightarrow \overrightarrow{PQ} =(0,0,-4)在\vec n的投影長=兩歪斜線L_1,L_2的距離 =稜邊長\\ ={|\overrightarrow{PQ} \cdot \vec n |\over |\vec n|} ={ 4\over \sqrt{6}} \Rightarrow 體積=\left( { 4\over \sqrt{6}}\right)^3 =\bbox[red, 2pt]{16\sqrt 6\over 9}\\ 註: 公布的答案是16\sqrt 2$$解答:$$由題意可知\cases{A=\begin{bmatrix} a & b\\ c& d\end{bmatrix} \\ A^{-1}=\begin{bmatrix} p & q\\ r& s\end{bmatrix}};現在\begin{bmatrix} a & b\\ c& d\end{bmatrix}\begin{bmatrix} 1 \\ 2\end{bmatrix} = \begin{bmatrix} 4 \\3 \end{bmatrix} \\\Rightarrow \begin{bmatrix} a & b\\ c& d\end{bmatrix}^{-1} \begin{bmatrix} a & b\\ c& d\end{bmatrix}\begin{bmatrix} 1 \\ 2\end{bmatrix} = \begin{bmatrix} a & b\\ c& d\end{bmatrix}^{-1} \begin{bmatrix} 4 \\3 \end{bmatrix} \Rightarrow \begin{bmatrix} 1 \\ 2\end{bmatrix} = \begin{bmatrix} a & b\\ c& d\end{bmatrix}^{-1} \begin{bmatrix} 4 \\3 \end{bmatrix} \\ \Rightarrow \begin{bmatrix} p & q\\ r &s \end{bmatrix} \begin{bmatrix} 4 \\3 \end{bmatrix}=\begin{bmatrix} 1 \\ 2\end{bmatrix} \Rightarrow (m,n)= \bbox[red,2pt]{(4,3)} 為\cases{pm+ qn=1\\ rm+sn = 2}的一解$$
解答:
$$\cases{雙曲線:{(x-5)^2 \over 81} -{y^2\over 64}=1 \Rightarrow 左頂點A(5-9,0)=(-4,0)\\ 橢圓:{x^2 \over 9}+{y^2\over 4}=1 \Rightarrow 左頂點C(-3,0)}\\,橢圓伸縮k倍後,C與A重疊,即橢圓a值由3變4\\ 因此{(kx)^2\over 9}+{(ky)^2\over 4}=1 \Rightarrow {x^2\over (3/k)^2} +{y^2\over (2/k)^2}=1 \Rightarrow {3\over k}=4 \Rightarrow k= \bbox[red, 2pt]{4\over 3}$$
解答:$$\cases{L:\cases{2x-y+3z=7 \cdots (1)\\ x-2y-bz=1 \cdots(2)} \\ L對稱比例式:{x-1\over a} ={y-1}= {z-k\over c} \cdots(3)},\quad由(3)知L經過(1,1,k)代入(1)\\ \Rightarrow 2-1+3k=7 \Rightarrow k=2; 再將(1,1,k) = (1,1,2)代入(2) \Rightarrow 1-2-2b=1 \Rightarrow b=-1\\ \Rightarrow L:\cases{2x-y+3z=7 \cdots (1)\\ x-2y+z=1 \cdots(2)} \Rightarrow {x+4\over 5}=y={y-5\over -3}\cdots(4);\\(3)與(4)有相同的方向向量,即(5,1,-3)=(a,1,c) \Rightarrow \cases{a=5\\ c=-3} \\ \Rightarrow a+b+c+k = 5-1-3+2 = \bbox[red, 2pt]{3}$$
解答:$$L':3x-4y=2 \Rightarrow P'(2,1)、Q'(-2,-2)在L'上;\\ A=\begin{bmatrix} 1& 2\\ 2 & 1 \end{bmatrix} \Rightarrow A^{-1} = \begin{bmatrix} -1/3 & 2/3\\ 2/3 & -1/3 \end{bmatrix} \Rightarrow \cases{A^{-1}P'=P=(0,1)\\ A^{-1}Q'=Q=(-2/3, -2/3)} \\ \Rightarrow L= \overleftrightarrow{PQ}: y={5\over 2}x+1 \Rightarrow \bbox[red, 2pt]{5x-2y+2=0}$$
解答:$$A=\begin{bmatrix} 0 & -1\\ 1 & 0\end{bmatrix} =\begin{bmatrix} \cos {\pi\over 2} & -\sin {\pi\over 2}\\ \sin {\pi\over 2} & \cos {\pi\over 2}\end{bmatrix} 相當於逆時鐘旋轉90^\circ,因此\cases{A^5=A \\A+ A^2+A^3 +A^4=0}\\ \Rightarrow A+ A^2 +\cdots +A^{10} = 2(A+ A^2+A^3+A^4) +A +A^2 =A +A^2 = \bbox[red, 2pt]{\begin{bmatrix} -1 & -1\\ 1 & -1\end{bmatrix}}$$
解答:
解答:$$A=\begin{bmatrix} 0 & -1\\ 1 & 0\end{bmatrix} =\begin{bmatrix} \cos {\pi\over 2} & -\sin {\pi\over 2}\\ \sin {\pi\over 2} & \cos {\pi\over 2}\end{bmatrix} 相當於逆時鐘旋轉90^\circ,因此\cases{A^5=A \\A+ A^2+A^3 +A^4=0}\\ \Rightarrow A+ A^2 +\cdots +A^{10} = 2(A+ A^2+A^3+A^4) +A +A^2 =A +A^2 = \bbox[red, 2pt]{\begin{bmatrix} -1 & -1\\ 1 & -1\end{bmatrix}}$$
解答:
$$\cases{O(-2,4,-1)\\ P(4,12,-1) \\ Q(-2,1, 3)}並令 \angle POQ的角平分線交\overline{PQ}於R(a,b,c),則\cases{\overline{OP} =10 \\ \overline{OQ} =5} \\ \Rightarrow {\overline{OP} \over \overline{OQ} }={\overline{PR} \over \overline{RQ} } ={10\over 5} ={2\over 1} \Rightarrow R={1\over 3}P+ {2\over 3}Q= (0,{14\over 3},{5\over 3}) \Rightarrow E之法向量:\overrightarrow{OR} =(2, {2\over 3}, {8\over 3}) \\ \Rightarrow E方程式:2(x+2) +{2\over 3}(y-4) +{8\over 3}(z+1)=0 \Rightarrow \bbox[red, 2pt]{3x+y+4z+6=0}$$
解答:$$過(2,0,0)及(0,4,2)之直線方程式: {x-2\over -2}={y\over 4} ={z\over 2} \\\Rightarrow 直線上的點P(-2t+2,4t,2t),t\in R 至y軸距離= \sqrt{(-2t+2)^2 +4t^2} =\sqrt{8t^2-8t+4} \\ \Rightarrow t=1/2時距離有最小值,此時P(1,2,1) \Rightarrow y軸上的點為\bbox[red,2pt]{(0,2,0)}$$
解答:$$E與F夾角30^\circ \Rightarrow \cos 30^\circ = {(1,1,1)\cdot (a,b,c) \over \sqrt{1^2+1^2+1^2}\times \sqrt{a^2+b^2+c^2}} \Rightarrow {\sqrt 3\over 2} ={a+b+c \over \sqrt 3\cdot \sqrt{a^2+b^2+c^2}} \\ \Rightarrow \sqrt{a^2+b^2+c^2} ={2\over 3}(a+b+c) \cdots(1)\\又\text{dist}(A,E)=3 \Rightarrow {|a+b+c-1| \over \sqrt{a^2+b^2+c^2}}=3 \Rightarrow \sqrt{a^2+b^2+c^2} ={1\over 3}|a+b+c-1|\cdots(2)\\ 將(1)代入(2) \Rightarrow {2\over 3}k = {1\over 3}|k-1|,其中k=a+b+c \Rightarrow {4\over9}k^2={1\over 9}(k^2-2k+1) \\ \Rightarrow 3k^2+2k-1=0 \Rightarrow k={-2\pm 4\over 6}=-1,{1\over 3} \Rightarrow a+b+c=\bbox[red, 2pt]{1\over 3}(-1不合,違反a+b+c >0)$$
解答:$$令M=\begin{vmatrix} a & b & c\\ 1 & 2 & 3\\ 3 & 2 & 1 \end{vmatrix} =-4a+8b-4c\\ 柯西不等式: (a^2+b^2 +c^2)((-4)^2 +8^2 +(-4)^2) \ge (-4a+8b-4c)^2 \Rightarrow 6\times 96 \ge M^2\\ \Rightarrow 24 \ge M \ge -24 \Rightarrow M之最大值為\bbox[red, 2pt]{24}$$
解答:$$假設\cases{\overline{AB}=a\\ \overline{AD}=b \\ A為原點} \Rightarrow \cases{A(0,0,0)\\ B(a,0,0)\\ C(a,b,0)\\ D(0,b,0)\\ P(0,0,h)},由\cases{\overline{PB}=2\sqrt 2\\ \overline{PC}=3 \\ \overline{PD}=\sqrt 5} \Rightarrow \cases{a^2+h^2=8 \\ a^2+b^2+h^2=9 \\ b^2+h^2=5}\\ \Rightarrow \cases{a=2\\b=1 \\h=2 (h=-2不影響結果)} \Rightarrow \cases{\overrightarrow{PB} = (2,0,-2)\\ \overrightarrow{PD} =(0,1,-2)} \Rightarrow \vec n=\overrightarrow{PB} \times \overrightarrow{PD} =(2,4,2)\\ \Rightarrow 平面PBD方程式: 2x+4y+2(z-2)=0 \Rightarrow x+2y+z=2 \\ \Rightarrow A至平面PBD距離={2\over \sqrt{6}} =\bbox[red, 2pt]{\sqrt 6 \over 3}$$
解答:$$\cases{{x^2\over a^2} +{y^2\over 4}=1 \\{x^2\over b^2}-{y^2\over 1}=1} 共焦點\Rightarrow \sqrt{a^2-4} =\sqrt{b^2+1} \Rightarrow a^2-b^2=5\\又\cases{依橢圓定義: \overline{PF_1} +\overline{PF_2}= 2a\\ 依雙曲線定義: \overline{PF_1}-\overline{PF_2}= 2b} \Rightarrow \cases{\overline{PF_1}=a+b\\ \overline{PF_2} =a-b} \Rightarrow \overline{PF_1}\times \overline{PF_2} = a^2-b^2= \bbox[red,2pt]{5}$$
解答:$$A(x_1,y_1) 在\Gamma上\Rightarrow {x_1^2\over 25} +{y_1^2\over 9}=1 \Rightarrow y_1^2= 9-{9\over 25}x_1^2;同理y_2^2=9-{9\over 25}x_2^2\\ 因此\cases{\overline{AF}=\sqrt{(x_1-4)^2+y_1^2} =\sqrt{(x_1-4)^2+9-{9\over 25}x_1^2} ={4\over 5}\sqrt{(x_1-{25\over 4})^2}\\ \overline{BF}=9/5\\ \overline{CF}={4\over 5}\sqrt{(x_2-{25\over 4})^2} }\\ 由於A,B皆在橢圓上,因此-4\le x_1,x_2\le 4 \Rightarrow \cases{x_1-{25\over 4} \lt 0 \\ x_2-{25\over 4}\lt 0} \Rightarrow \cases{\overline {AF} = {4\over 5}({25\over 4}-x_1) \\ \overline{BF} ={4\over 5}({25\over 4}-x_2)}\\ \overline{AF},\overline{BF},\overline{CF} 等差\Rightarrow \overline{AF}+\overline{CF} =2\overline{BF} \Rightarrow {4\over 5}({25\over 2}-x_1-x_2) ={18\over 5} \\ \Rightarrow {25\over 2}-x_1-x_2={9\over 2} \Rightarrow x_1+x_2 = {25\over 2}-{9\over 2} =\bbox[red, 2pt]{8}$$
解答:$$E與F夾角30^\circ \Rightarrow \cos 30^\circ = {(1,1,1)\cdot (a,b,c) \over \sqrt{1^2+1^2+1^2}\times \sqrt{a^2+b^2+c^2}} \Rightarrow {\sqrt 3\over 2} ={a+b+c \over \sqrt 3\cdot \sqrt{a^2+b^2+c^2}} \\ \Rightarrow \sqrt{a^2+b^2+c^2} ={2\over 3}(a+b+c) \cdots(1)\\又\text{dist}(A,E)=3 \Rightarrow {|a+b+c-1| \over \sqrt{a^2+b^2+c^2}}=3 \Rightarrow \sqrt{a^2+b^2+c^2} ={1\over 3}|a+b+c-1|\cdots(2)\\ 將(1)代入(2) \Rightarrow {2\over 3}k = {1\over 3}|k-1|,其中k=a+b+c \Rightarrow {4\over9}k^2={1\over 9}(k^2-2k+1) \\ \Rightarrow 3k^2+2k-1=0 \Rightarrow k={-2\pm 4\over 6}=-1,{1\over 3} \Rightarrow a+b+c=\bbox[red, 2pt]{1\over 3}(-1不合,違反a+b+c >0)$$
解答:$$令M=\begin{vmatrix} a & b & c\\ 1 & 2 & 3\\ 3 & 2 & 1 \end{vmatrix} =-4a+8b-4c\\ 柯西不等式: (a^2+b^2 +c^2)((-4)^2 +8^2 +(-4)^2) \ge (-4a+8b-4c)^2 \Rightarrow 6\times 96 \ge M^2\\ \Rightarrow 24 \ge M \ge -24 \Rightarrow M之最大值為\bbox[red, 2pt]{24}$$
解答:$$假設\cases{\overline{AB}=a\\ \overline{AD}=b \\ A為原點} \Rightarrow \cases{A(0,0,0)\\ B(a,0,0)\\ C(a,b,0)\\ D(0,b,0)\\ P(0,0,h)},由\cases{\overline{PB}=2\sqrt 2\\ \overline{PC}=3 \\ \overline{PD}=\sqrt 5} \Rightarrow \cases{a^2+h^2=8 \\ a^2+b^2+h^2=9 \\ b^2+h^2=5}\\ \Rightarrow \cases{a=2\\b=1 \\h=2 (h=-2不影響結果)} \Rightarrow \cases{\overrightarrow{PB} = (2,0,-2)\\ \overrightarrow{PD} =(0,1,-2)} \Rightarrow \vec n=\overrightarrow{PB} \times \overrightarrow{PD} =(2,4,2)\\ \Rightarrow 平面PBD方程式: 2x+4y+2(z-2)=0 \Rightarrow x+2y+z=2 \\ \Rightarrow A至平面PBD距離={2\over \sqrt{6}} =\bbox[red, 2pt]{\sqrt 6 \over 3}$$
解答:$$\cases{{x^2\over a^2} +{y^2\over 4}=1 \\{x^2\over b^2}-{y^2\over 1}=1} 共焦點\Rightarrow \sqrt{a^2-4} =\sqrt{b^2+1} \Rightarrow a^2-b^2=5\\又\cases{依橢圓定義: \overline{PF_1} +\overline{PF_2}= 2a\\ 依雙曲線定義: \overline{PF_1}-\overline{PF_2}= 2b} \Rightarrow \cases{\overline{PF_1}=a+b\\ \overline{PF_2} =a-b} \Rightarrow \overline{PF_1}\times \overline{PF_2} = a^2-b^2= \bbox[red,2pt]{5}$$
解答:$$A(x_1,y_1) 在\Gamma上\Rightarrow {x_1^2\over 25} +{y_1^2\over 9}=1 \Rightarrow y_1^2= 9-{9\over 25}x_1^2;同理y_2^2=9-{9\over 25}x_2^2\\ 因此\cases{\overline{AF}=\sqrt{(x_1-4)^2+y_1^2} =\sqrt{(x_1-4)^2+9-{9\over 25}x_1^2} ={4\over 5}\sqrt{(x_1-{25\over 4})^2}\\ \overline{BF}=9/5\\ \overline{CF}={4\over 5}\sqrt{(x_2-{25\over 4})^2} }\\ 由於A,B皆在橢圓上,因此-4\le x_1,x_2\le 4 \Rightarrow \cases{x_1-{25\over 4} \lt 0 \\ x_2-{25\over 4}\lt 0} \Rightarrow \cases{\overline {AF} = {4\over 5}({25\over 4}-x_1) \\ \overline{BF} ={4\over 5}({25\over 4}-x_2)}\\ \overline{AF},\overline{BF},\overline{CF} 等差\Rightarrow \overline{AF}+\overline{CF} =2\overline{BF} \Rightarrow {4\over 5}({25\over 2}-x_1-x_2) ={18\over 5} \\ \Rightarrow {25\over 2}-x_1-x_2={9\over 2} \Rightarrow x_1+x_2 = {25\over 2}-{9\over 2} =\bbox[red, 2pt]{8}$$


























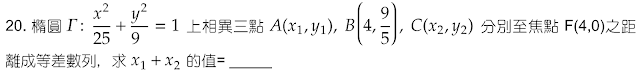
你好:第5題的計算有點問題,另外,R1-R2+R3-R4的區塊應該是中間長條形棕色和藍色的總面積吧?(可是我不會算)謝謝
回覆刪除