94年第一次國民中學學生基本學力測驗
試題來源:師大心測中心如果你會手算開根號:
故選(C)。$$否則只好:\cases{21^2=441\\ 22^2=484\\ 23^2=529\\ 24^2=576} \Rightarrow 530最接近23^2,故選\bbox[red,2pt]{(C)}$$
解:
故選(B)。
解:
解:
解:
比30大的質數: 31, 37, 41..., 因此c介於37與41之間,故選(A)。
解:
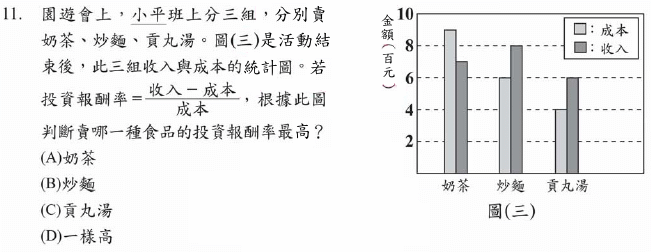
奶茶是虧本的,炒麵及貢丸湯的(收入-成本)都是(8-6)=2,但貢丸湯成本較低,所以報酬率較高,故選(C)。
故選(B)。
解:
比30大的質數: 31, 37, 41..., 因此c介於37與41之間,故選(A)。
解:
奶茶是虧本的,炒麵及貢丸湯的(收入-成本)都是(8-6)=2,但貢丸湯成本較低,所以報酬率較高,故選(C)。
解:
(A)在150~160公分之間的人數=25,佔全班25/50=50%;
(B)在130~150公分之間的人數=2+13=15,佔全班15/50=30%;
(C)在130~160公分之間的人數=2+13+25=40,佔全班40/50=80%;
(D)在140~160公分之間的人數=13+25=38,佔全班38/50=76%;
只有(B)錯誤,故選(B)。
(A)在150~160公分之間的人數=25,佔全班25/50=50%;
(B)在130~150公分之間的人數=2+13=15,佔全班15/50=30%;
(C)在130~160公分之間的人數=2+13+25=40,佔全班40/50=80%;
(D)在140~160公分之間的人數=13+25=38,佔全班38/50=76%;
只有(B)錯誤,故選(B)。
假設一顆玻璃珠的體積為a。
三個相同的玻璃珠放入水中,結果水沒有滿⇒3a<(450-300)⇒3a<150⇒a<50;
再加兩個放入水中,結果水滿溢出⇒5a>(450-300)⇒5a>150⇒ a>30;
因此30<a<50,故選(A)。
對稱軸為\(\overline{AC}\),故選\(\bbox[red,2pt]{(D)}\)
令速率為a,則各段距離如下圖:
乙丁距離的平方=(8a)2+(15a)2=289a2⇒ 乙丁距離=17a⇒甲丁距離 = 8a+17a=25a⇒需要25分鐘,故選(C)。
解:
此題相當於以A為圓心半徑為1.5畫圓、以B為圓心半徑為3畫圓,兩圓的交點就是C,如下圖:
故選(D)。
解:
直角△ABP中,BP=3, AP=5⇒AB=4
△ABP與△ACQ相似(∠BAP=∠PAC,∠C=∠B=90°) ⇒ AC:CQ = AB:BP ⇒ AC:9 = 4:3 ⇒AC=12⇒AQ=15⇒PQ=15-5=10,故選(B)。
解:
△EFG+△GHI+△IJK=DE×(JI+HG+FE)/2 = AB×BK/2=△ABK
面積比=1:1,故選(A)。
7:00~9:00 每5分鐘發一車:
07:00、07:05、...、07:30、07:35、07:40、07:45、07:50、07:55,共12班(藍色有5班)
08:00、08:05、...、08:55,共12班
09:00~ 每15分鐘發一車:
09:00、09:15、09:30、09:45、10:00、...(藍色有3班)
因此7:34~9:34共發車5+12+3=20,故選(C)。
解:
甲乙丙丁都有一邊等長,還有兩個直角,但面積均不相同,所以均不相似,故選(D)。
解:
(甲、乙)=(613、136)、(623、236)、(633、336)、(643、436)、(653、536)、(663、636)、(673、736)、(683、836)、(693、936),其中甲>乙共有6種數字,所以機率為6/9=2/3,故選(C)。
甲乙丙丁都有一邊等長,還有兩個直角,但面積均不相同,所以均不相似,故選(D)。
解:
(甲、乙)=(613、136)、(623、236)、(633、336)、(643、436)、(653、536)、(663、636)、(673、736)、(683、836)、(693、936),其中甲>乙共有6種數字,所以機率為6/9=2/3,故選(C)。
解:
兩兄妹的年齡隨著時間遞增,且一年增一歲,即斜率為1。
故選(C)。
解:
3,3,6雖為等腰,但3+3沒有大於6,因此(A)錯誤;
6,6,3為等腰三角形,因此(B)正確;
3×3+3√3×3√3=36=6×6,故(C)正確;
3×3+6×6=45=3√5×3√5,故(D)正確;
選(A)。
解:
五個正方形總和=y-18+y-9+y+y+9+y+18 = 5y,故選(A)。
解:
假設白繩長度a、紅繩長度b,如下圖:
故選(B)。
解:
假設相遇A點,如下圖,則∠A=180-70-60=50。
大角對大邊,所以紅線>藍線>黑線=200,故選(A)。
解:
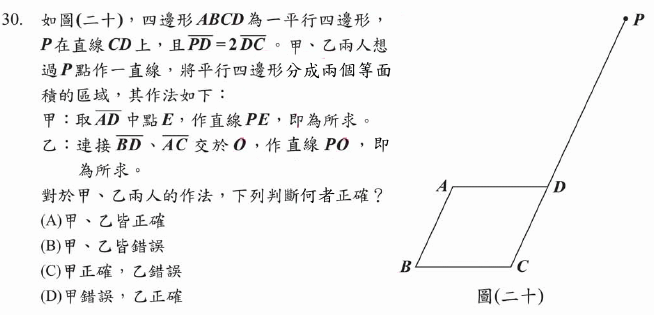
甲的作法如下圖,由於FE與AB不平行,所以無法均分ABCD
乙的作法如下圖:△AOB與△COD全等(SSS):AO=OC、BO=OD、AB=CD
△AOH與△COG全等(ASA):∠GCO=∠OAH(內錯角)、AO=OC、∠COG = ∠HOA
△BOG與△DOH全等(ASA):∠HDO=∠OBG(內錯角)、DO=OB、∠DOH = ∠GOB
因此ABGH面積=GHDC面積,所以乙作法正確。
故選(D)。
解:
上圖全部面積=紅色矩形+半圓=1×2+π/2=2+π/2
上圖斜線面積=全部面積-兩個四分之一圓=(2+π/2)-π/2=2
圖(廿一)的斜線面積相當於上圖四個斜線面積=2×4=8,故選(B)。
※請閱讀下列的敘述後,回答第32.題和第33.題
解:矩形OECF的兩對角線等長,即EF=OC=半徑=a,故選(A) 。
解:
由於OA=OB=b⇒△OAB為等腰直角三角形⇒△FCA也是等腰直角三角形⇒FO+FC=FO+FA=b⇒OFCE周長=2(FO+FC)=2b,故選(B)。
















































第10題有沒有簡單的詳解呢?
回覆刪除