95年第一次國民中學學生基本學力測驗
試題來源: 師大心測中心解:
原式= (-12)+[(-18)÷(-6)]-[(-3)×2] = (-12)+[3]-[-6] =-12+3+6 =-3,故選(B)。
解:
2/25 = 8/100 = 0.08 = 8×10-2,故選(B)。
西元2005年的市場佔有率為20%,西元2000年的市場佔有率為2%,0.2/0.02=10,故選(C)。
骰子丟出1、2、...、6的機率皆是1/6,故選(D)。
解:
各三角形的內角
甲(45, 55, 80)、乙(45, 55, 80)、丙(45, 55, 80)、丁(55, 60, 65)、戊(45, 55, 80)。只有丁與其它四個三角形不同,故選(D)。
甲(45, 55, 80)、乙(45, 55, 80)、丙(45, 55, 80)、丁(55, 60, 65)、戊(45, 55, 80)。只有丁與其它四個三角形不同,故選(D)。
解:
由於 PQ距離=2.4-(-1.3)=3.7、PR距離=3.7-(-1.3)=5,所以公車在QR之間,故選(D)。
解:
231192 = 19×9×1352=19×9×8×169=23×32×132×19,因此a=3, c=13,a+c=16,故選(C)。
除法不可前後對調,故選(D)。
灰色面積相當一個半徑為1的圓面積=π。
BD長度=2⇒以BD為直徑之圓面積,其半徑=2/2=1,面積為π,故選(A)。
解:
70分→6人、75分→12人、80分→8人、85分→8人、90分→12人、95分→6人。總平均= (70×6+75×12+ 80×8+85×8+ 90×12+ 95×6) / (6+12+8+8+12+6) = 4290 / 52 = 82.5,故選(C)。
4x2-16x+15=(2x-5)(2x-3),兩根為5/2及3/2,故選(A)。
解:
假設買a支原子筆,則鉛筆a+3枝,共花費30a+17(a+3) ≤ 200 ⇒47a+51≤ 200 ⇒ a≤(149/47) = 3.17..,故選(B)。
解:
直接代入各選項,可得 (A) 5≤4-2x=4+6=10,故選(A)。
解:
∠ABD+∠ADB=90°⇒扇形甲+扇形乙=四分之一圓=8×8×π/4 = 16π;△BCD面積=矩形面積的一半=8×5π/2=20π。
灰色區域的面積=矩形面積-(扇形甲+扇形乙)-△BCD面積 = 40π-16π-20π=4π,故選(A)。
直線通過 (0, a)及(a/3, 0) 即 (0, 正)及(正, 0),因此不通過第三象限,故選(C)。
Q為重心⇒AR=RC,故選(B)。
假設漱口水瓶容量為A、瓶蓋容量為a。使用10次的用量=(a/2)×10=5a = A/4 ⇒ a = A/20;
漱口水剩下 (3/4)A,一次用量為1/3 瓶蓋= (A/20)/3 = A/60 ⇒ 還可用 (3/4)A / (A/60) = 45 次,故選(B)。
漱口水剩下 (3/4)A,一次用量為1/3 瓶蓋= (A/20)/3 = A/60 ⇒ 還可用 (3/4)A / (A/60) = 45 次,故選(B)。
E、F為切點⇒CF=CE=a;D、F為切點⇒BF=BD=b;
D、E為切點⇒AD=AE⇒AB+BD=AC+CE⇒3+b=4+a ---(1)
BC=BF+FC⇒b+a=5 ---(2)
D、E為切點⇒AD=AE⇒AB+BD=AC+CE⇒3+b=4+a ---(1)
BC=BF+FC⇒b+a=5 ---(2)
由(1)及(2)可求得a=2, b=3。
BE2=AB2+AE2=32+(4+2)2=45,故選(C)。
甲+乙=BC2+CD2=AD2+CD2=AC2=(1.5+1.5)2=9,故選(D)。
四個角對應相同的圓弧,且B與C皆在圓周上,所以∠2=∠4;
∠1在圓內、∠3在圓外,所以∠1>∠2=∠4>∠3,故選(A)。
∠1在圓內、∠3在圓外,所以∠1>∠2=∠4>∠3,故選(A)。
解:
假設一杯豆漿售價a元
(A) 24杯=12×第1杯原價,第2杯半價=12×1.5a=18a
(B) 24杯=8×第1、2杯原價,第3杯免費=8×2a=16a
(C)甲店買12杯=6×1.5a=9a, 乙店買12杯=4×2a=8a, 合計17a
(D) 甲店買6杯=3×1.5a=4.5a, 乙店買18杯=6×2a=12a, 合計16.5a
因此全部在乙店買花錢最少,故選(B)。
(A) 24杯=12×第1杯原價,第2杯半價=12×1.5a=18a
(B) 24杯=8×第1、2杯原價,第3杯免費=8×2a=16a
(C)甲店買12杯=6×1.5a=9a, 乙店買12杯=4×2a=8a, 合計17a
(D) 甲店買6杯=3×1.5a=4.5a, 乙店買18杯=6×2a=12a, 合計16.5a
因此全部在乙店買花錢最少,故選(B)。
解:
乙車剛好繞完第三圈費時20×3=60分鐘,60分鐘相當於甲車繞60/35=1又5/7圈,其中 2/4<5/7 < 3/4,因此甲車位於第三象限,故選(C)。
解:
顯然L1是、L2不是對稱軸,故選(B)。
解:
60/45 = (4×15)/(3×15)⇒15個圖(十四)拼湊起來⇒15×6=90,故選(C)。解:
三月男性x人⇒三月女性2040-x人;
四月男性增加x(1/5)人、四月女性減少(2040-x)(1/7)人⇒四月人口變動x(1/5)-(2040-x)(1/7)= -30,故選(A)。
;
解:$$a,b為(x-29)^2=247的兩根\Rightarrow \cases{(a-29)^2=247 \\ (b-29)^2=247} \Rightarrow \cases{\pm(a-29)為247的平方根 \\ \pm(b-29)為247的平方根 } \\ \Rightarrow 29-b為247的平方根,故選\bbox[red,2pt]{(D)}$$
對於兩人的作法,下列判斷何者正確?
(A) 兩人都正確 (B) 兩人都錯誤
(C) 甲正確,乙錯誤 (D) 甲錯誤,乙正確
解:
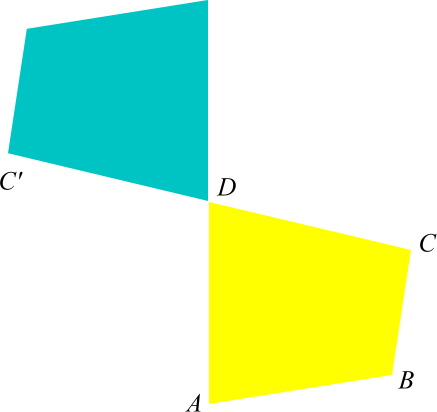
乙的作法相當於以D為圓心,逆時鐘旋轉180度。DC旋轉後仍為一直線,如下圖,所以乙的作法正確。
對於兩人的作法,下列判斷何者正確?
(A) 兩人都正確 (B) 兩人都錯誤
(C) 甲正確,乙錯誤 (D) 甲錯誤,乙正確
甲的作法顯然錯誤,如下圖:
乙的作法相當於以D為圓心,逆時鐘旋轉180度。DC旋轉後仍為一直線,如下圖,所以乙的作法正確。
故選(D)。
解:
$$\triangle ABE為等腰直角且\overline{AB}=\overline{AE} \Rightarrow \overline{BE}=\sqrt 2 \\\Rightarrow \cases{戊 =1\times 1=1 \\ 乙=2\triangle ABE +矩形BCDE =2\times ({1\over 2}\times 1\times 1)+\sqrt 2\times 1=1+\sqrt 2} \\ \Rightarrow {戊\over 甲} ={戊\over 乙} ={1\over 1+\sqrt 2},故選\bbox[red,2pt]{(D)}$$
-- END --









































第33題搞錯囉~六邊形每邊邊長都是1
回覆刪除可以參考這個:
http://a8802020.pixnet.net/blog/post/24282953-95-年第一次基測數學的詳解
感謝您的提醒,第33題已修訂!
刪除