95年大學指考數學乙詳解

95學年度指定科目考試試題

數學乙

第壹部分：選擇題
一、單選題

解：

$$圓(x-3)^2+(y-4)^2=5^2 \Rightarrow \cases{圓心O(3,4) \\ 半徑r=5},若圓心至直線的距離等於半徑長,則圓與該直線相切;\\ (1) \left| \cfrac{9+16-5}{\sqrt{3^2+4^2}}\right| =\cfrac{20}{5}=4 \ne 5 \\ (2) \left|\cfrac{9+16-0}{\sqrt{3^2+4^2}}\right| =\cfrac{25}{5}=5 \\(3) \left|\cfrac{12+12-5}{\sqrt{3^2+4^2}}\right| =\cfrac{19}{5} \ne 5 \\(4) \left|\cfrac{12+12-0}{\sqrt{3^2+4^2}}\right| =\cfrac{24}{5} \ne 5 \\(5) \left|\cfrac{12+12-1}{\sqrt{3^2+4^2}}\right| =\cfrac{23}{5} \ne 5\\，故選\bbox[red, 2pt]{(2)}$$

---

2. 某 大 學 數 學 系 甄 選 入 學 的 篩 選 方 式 如 下 ：
先 就 學 科 能 力 測 驗 國 文、英 文 和 社 會 這 三 科 成 績（ 級 分 ）加 總 做 第 一 次 篩 選 。
然 後 從 通 過 篩 選 的 學 生 當 中 ， 以 自 然 科 的 成 績 做 第 二 次 篩 選 。
最 後 再 從 通 過 的 學 生 當 中 ， 以 數 學 科 的 成 績 做 第 三 次 篩 選 ， 選 出 一 些 學 生 參加 面 試 。
現 在 有 五 位 報 名 該 系 的 學 生 的 學 科 能 力 測 驗 成 績 如 下 表 ：

已 知 這 五 位 學 生 當 中 ， 通 過 第 一 次 篩 選 的 有 四 位 ， 通 過 第 二 次 篩 選 的 有 三位 ， 通 過 第 三 次 篩 選 可 以 參 加 面 試 的 只 剩 下 一 位 。 請 問 哪 一 位 學 生 參 加 面
試 ？

(1) 甲 (2) 乙 (3) 丙 (4) 丁 (5) 戊

解：

$$\begin{array}{c|rrrrr|c}學生 & 國 & 英 & 數 &社 & 自 &國+英+社 \\\hline 甲 & 13 & 8 & 14 & 15 & 11 & 36\\\hline 乙& 12 & 12 & 12 & 12& 12& 36 \\\hline 丙& 9 & 13 & 15 & 8 & 15 & 30 \\\hline 丁& 11 & 12 & 13 &10 & 13 & 33 \\\hline 戊& 13 & 15& 11 & 7 & 12 & 35\\\hline\end{array} \Rightarrow 國+英+社: 甲 = 乙>戊 >丁>丙\\ \Rightarrow 第一次篩選剩下甲乙戊丁四人 \Rightarrow  自然級分: 丁>乙=戊> 甲 \Rightarrow 第二次篩選剩下乙丁戊三人\\ \Rightarrow 數學級分:丁>乙>戊 \Rightarrow 丁參加面試，故選\bbox[red,2pt]{(4)}$$

---

解： $$r=0 \Rightarrow \vec a+\vec b+r\vec c= \vec a+\vec b= (1,2,1)\ne \vec 0，故選\bbox[red,2pt]{(2)}$$

---

二、多選題
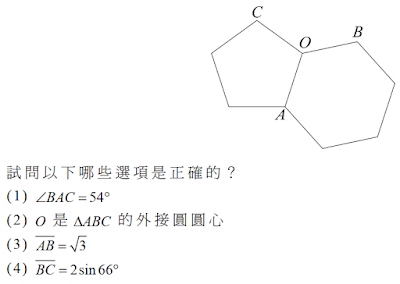
4. 嘌 呤 是 構 成 人 體 基 因 的 重 要 物 質 ，它 的 化 學 結 構 式 主 要 是 由 一 個 正 五 邊 形 與一 個 正 六 邊 形 構 成 （ 令 它 們 的 邊 長 均 為 1） 的 平 面 圖 形 ， 如 下 圖 所 示 ：

解：

$$(1)\times: \cases{正5邊形每個內角為(5-2)\times 180\div 5=108度 \\ 正6邊形每個內角為(6-2)\times 180\div 6=120度 } \Rightarrow \cases{\angle COA=108^\circ \\ \angle AOB=120^\circ}\\ \qquad 又\cases{\overline{OC}= \overline{OA} \Rightarrow \angle CAO = (180^\circ- \angle COA)\div 2= (180^\circ-108^\circ)\div 2=36^\circ \\ \overline{OA}= \overline{OB} \Rightarrow \angle OAB = (180^\circ- \angle AOB)\div 2= (180^\circ-120^\circ)\div 2=30^\circ \\} \\ \qquad \Rightarrow \angle BAC= \angle CAO+\angle OAB = 36^\circ + 30^\circ = 66^\circ \\(2) \bigcirc: \overline{OA}= \overline{OB}=\overline{OC} =1\Rightarrow O是外接圓圓心 \\ (3) \bigcirc: \cases{D為\overline{AB}中點 \\ \angle OBA=30^\circ} \Rightarrow \overline{BD} = \overline{OB} \times {\sqrt 3\over 2} = {\sqrt 3\over 2} \Rightarrow \overline{AB}= \overline{BD}\times 2=\sqrt 3 \\ (4) \bigcirc: \cases{E為\overline{BC}中點\\ \angle BOC=360^\circ - 120^\circ - 108^\circ = 132^\circ} \Rightarrow \angle BOE= 132^\circ \div 2=66^\circ \\\qquad \Rightarrow \overline{BE}= \overline{OB} \sin 66^\circ = \sin 66^\circ \Rightarrow \overline{BC}= 2\overline{BE}= 2\sin 66^\circ\\，故選\bbox[red,2pt]{(2,3,4)}$$

---

5. 一 個「 訊 息 」是 由 一 串 5 個 數 字 排 列 組 成 ， 且 每 位 數 字 都 只 能 是 0 或 1， 例 如10010 與 01011 就 是 兩 個 不 同 的 訊 息 。 兩 個 訊 息 的 「 距 離 」 定 義 為 此 兩 組 數字 串 相 對 應 位 置 中 ， 數 字 不 同 的 位 置 數 。 例 如 ， 數 字 串 10010 與 01011 在 第1, 2 及 5 三 個 位 置 不 同 ， 所 以 訊 息 10010 與 01011 的 距 離 為 3。
試 問 以 下 哪 些 選 項 是 正 確 的 ？

(1) 與 訊 息 10010 相 距 最 遠 的 訊 息 為 11101
(2) 任 兩 訊 息 之 間 的 最 大 可 能 距 離 是 4
(3) 與 訊 息 10010 相 距 為 1 的 訊 息 恰 有 5 個
(4) 與 訊 息 10010 相 距 為 2 的 訊 息 恰 有 9 個

解： $$(1) \times: \cases{10010 與 11101的距離為4 \\ 10010 與 01101的距離為5} \Rightarrow 11101不是最遠的訊息 \\(2) \times: 只要將0換成1、1換0，則長度為5的最大距離為5 \\(3) \bigcirc:相距為1 \Rightarrow 5個數字中有1個不同 \Rightarrow 共有5種可能 \\(4) \times: 相距為2 \Rightarrow 5個數字中有2個不同 \Rightarrow 共有C^5_2=10種可能\\故選\bbox[red,2pt]{(3)}$$

---

解：
$$(1) \bigcirc: \cases{-15 \le x\le 15 \\ -10 \le y \le 10} \xrightarrow {三分之一} \cases{-15 \times 3\le x\le 15 \times 3 \\ -10\times 3 \le y \le 10 \times 3} \Rightarrow \cases{-45 \le x\le 45 \\ -30 \le y \le 30}\\(2) \times: 長寬比不變則斜率不變 \\(3) \bigcirc:\cases{y=x^2-30x+190 \\ y=5x-60} \Rightarrow x^2-30x+190=5x-60 \Rightarrow x^2-35x+250=0 \\ \qquad \Rightarrow (x-25)(x-10)=0 \Rightarrow \cases{x=10 \\x=25 } \Rightarrow \cases{y=5\times 10-60=-10 \\ y=5\times 25-60 =65} \\ \qquad \Rightarrow 兩圖形的交點為\cases{A(10,-10) \Rightarrow \cases{-15 \le 10 \le 15\\ -10\le -10 \le 10}\\ B(25,65) \Rightarrow \cases{25 \not \le 15\\ 65 \not \le 10}} \Rightarrow 只有一點A在預設視窗內 \\(4) \times: \cases{-15 \le x\le 15 \\ -10 \le y \le 10} \xrightarrow {五分之一} \cases{-15 \times 5\le x\le 15 \times 5 \\ -10\times 5 \le y \le 10 \times 5} \Rightarrow \cases{-75 \le x\le 75 \\ -50 \le y \le 50} \\\qquad \Rightarrow B(25,65) 的y坐標65 \not \le 50 \Rightarrow 仍然只有一個交點在視窗內\\ 故選\bbox[red,2pt]{(1,3)}$$

---

7. 某 次 數 學 測 驗 分 為 選 擇 題 與 非 選 擇 題 兩 部 分 。 下 列 的 散 佈 圖 中 每 個 點 (X  , Y) 分 別 代 表 一 位 學 生 於 此 兩 部 分 的 得 分 ， 其 中 X 表 該 生 選 擇 題 的 得 分 ， Y 表該 生 非 選 擇 題 的 得 分 。 設

Z = X +Y

為 各 生 在 該 測 驗 的 總 分 。 共 有 11 位 學 生 的 得 分 數 據 。

試 問 以 下 哪 些 選 項 是 正 確 的 ？
(1) X 的 中 位 數 > Y 的 中 位 數
(2) X 的 標 準 差 > Y 的 標 準 差
(3) X 的 全 距 > Y 的 全 距
(4) Z 的 中 位 數 = X 的 中 位 數 + Y 的 中 位 數

解：

$$(1) \bigcirc: 有11個數字，中位數位於第6個；由上圖可知：X的中位數為35，Y的中位數約為28\\ \qquad，因此X的中位數>Y的位數\\ (2) \bigcirc:由圖形可知: \cases{15\le X\le 48 \\ 22\le Y\le 36} \Rightarrow X值變動較大 \Rightarrow X的標準差 > Y的標準差 \\ (3) \bigcirc:  \cases{15\le X\le 48 \\ 22\le Y\le 36} \Rightarrow \cases{X的全距約為33 \\ Y的全距約為14} \Rightarrow X的全距 > Y的全距\\ (4) \times: Z=X+Y =\{15+22=37,20+26=46, 25+32=57 ,27+25=52, 30+27=57\\ \qquad , 36+25=61, 35+35=70, 37+36=73, 41+28=69, 45+33=78, 48+36=84 \}\\\qquad \Rightarrow Z的中位數為61，而X的中位數35+Y的中位數28=63，兩者不相等\\ 故選\bbox[red,2pt]{(1,2,3)}$$

---

三、選填題

解：

$$假設長方形邊長分別為a及b，見上圖 \Rightarrow 2a+2b-2=66 \Rightarrow a+b=34 \Rightarrow \cfrac{a+b}{2} \ge \sqrt {ab} \\  \Rightarrow 17^2 \ge ab  \Rightarrow 菜圃面積 = ab  的 最大值為17^2 =  \bbox[red, 2pt]{289}平方公尺$$

---

解：

$$大樓高度最高為h=3000\tan 8^\circ = 3000\times 0.1405 =421.5公尺， 相當於\cfrac{421.5} {5} = 84.3層樓\\ \Rightarrow 最多可蓋\bbox[red, 2pt]{84}樓$$

---

解：

$$7色挑6色排列，有P^7_6排法；由於是環狀排列，因此有\cfrac{P^7_6}{6} =\bbox[red, 2pt]{840}種排法$$

---

第貳部份：非選擇題

解：

$$(1) 1521 = 3\times 3\times 13\times 13 \Rightarrow \sqrt{1521}=3\times 13=\bbox[red, 2pt]{39}\\(2)  假設球台左下角為坐標原點\Rightarrow \cases{甲(23,39.5) \\ 乙(40,27.5)\\ 鈔票中心C(8,3.5)} \Rightarrow \overline{甲C}= \sqrt{(23-8)^2 +(39.5-3.5)^2}\\ \qquad =\sqrt{1521} =\bbox[red, 2pt]{39} \\(3) \overline{乙C}= \sqrt{32^2+24^2} =40 > \overline{甲C} \Rightarrow \bbox[red, 2pt]{甲}獲勝$$

---

二、 為 預 防 禽 流 感 ， 營 養 師 吩 咐 雞 場 主 人 每 天 必 須 從 飼 料 中 提 供 至 少 84 單 位 的營 養 素 A、 至 少 72 單 位 的 營 養 素 B 和 至 少 60 單 位 的 營 養 素 C 給 他 的 雞 群 。這 三 種 營 養 素 可 由 兩 種 飼 料 中 獲 得，且 知 第 一 種 飼 料 每 公 斤 售 價 5 元 並 含 有7 單 位 的 營 養 素 A， 3 單 位 的 營 養 素 B 與 3 單 位 的 營 養 素 C； 第 二 種 飼 料 每公 斤 售 價 4 元 並 含 有 2 單 位 的 營 養 素 A， 6 單 位 的 營 養 素 B 與 2 單 位 的 營 養素 C。
(1) 若 雞 場 主 人 每 天 使 用 x 公 斤 的 第 一 種 飼 料 與 y 公 斤 的 第 二 種 飼 料 就 能 符
合 營 養 師 吩 咐 ， 則 除 了 $x\ge 0, y\ge 0$兩 個 條 件 外 ， 寫 下 x, y 必 須 滿 足 的 不 等
式 組 。 （ 3分 ）
(2) 若 雞 場 主 人 想 以 最 少 的 飼 料 成 本 來 達 到 雞 群 的 營 養 要 求 ， 則 x, y 的 值 為
何 ？ 最 少 的 飼 料 成 本 又 是 多 少 ？

解：

$$(1)\cases{x公斤的第1種飼料產生產生\cases{維生素A:7x單位 \\ 維生素B:3x單位 \\維生素C:3x單位 } \\ y公斤的第2種飼料產生產生\cases{維生素A:2y單位 \\ 維生素B:6y單位 \\維生素C:2y單位 }} \Rightarrow \bbox[red, 2pt]{\cases{7x+2y \ge 84 \\ 3x+6y \ge 72 \\ 3x+2y \ge 60}} \\(2)\cases{7x+2y = 84 \\ 3x+6y = 72 \\ 3x+2y = 60\\ x=0 \\ y=0} \Rightarrow 交點\cases{A(0,42) \\B(6,21) \\ C(18,3) \\ D(24,0)},今f(x,y)=5x+4y \Rightarrow \cases{f(A)=168 \\ f(B)=114 \\ f(C)=102 \\ f(D)=120} \\ \qquad \Rightarrow 當\bbox[red, 2pt]{\cases{x=18\\ y=3}} 有最小成本\bbox[red, 2pt]{102}元$$

---

-- END   (僅供參考)  --