110年試辦考試(適用於108課綱)數學A
第壹部分、選擇(填)題
一、單選題
解答:$$\cases{\log(2+\sqrt 3)\\ \log(2-\sqrt 3) \\-\log(2+\sqrt 3)=\log({1\over 2+\sqrt 3}) =\log (2-\sqrt 3) \\ -\log(2-\sqrt 3) =\log({1\over 2-\sqrt 3}) =\log (2+\sqrt 3)\\ \log 2+\log \sqrt 3= \log 2\sqrt 3} \Rightarrow 有3個不同的實數,故選\bbox[red,2pt]{(3)}$$解答:$$|x-10| \lt |x-60| \lt |x+10| \Rightarrow \begin{cases} x-10\lt x-60 \lt x+10 & \text{if }x\ge 60 \\ x-10\lt 60-x \lt x+10 & \text{if } 10\le x\le 60 \\ 10-x\lt 60-x \lt x+10 & \text{if }-10\le x\le 10 \\ 10-x \lt 60-x \lt -x-10 & \text{if } x\le -10\end{cases} \\ \Rightarrow \cases{無解\\ 25\lt x\lt 35\\ 無解\\ 無解} \Rightarrow 25\lt x\lt 35 \Rightarrow x=26,27,\dots,34,共9個整數解,故選\bbox[red,2pt]{(2)}$$
解答:$$兩中線\cases{8x+5y=14 \\ x+7y=6}交點為P({4\over 3},{2\over 3}) \\\Rightarrow 過A(2,3)及P({4\over 3},{2\over 3})的直線斜率為{3-2/3\over 2-4/3} ={7/3 \over 2/3}={7\over 2},故選\bbox[red,2pt]{(1)}$$
解答:$$令\cases{A(1,0,-1)\\ B(1,-1,0)\\ L:{1\over 2}x-{13\over 7}=y+19 =-2z} \Rightarrow \cases{\overrightarrow{AB}= (0,-1,1)\\ L方向向量=\vec u=(2,1,-{1\over 2})} \\ \Rightarrow E的法向量\vec n= \overrightarrow{AB}\times \vec u =(-{1\over 2},2,2) \Rightarrow |\vec n|={\sqrt{33}\over 2} \\ \Rightarrow \cases{(1):\cos \theta={(1,0,0)\cdot \vec n\over |\vec n|}=-{1\over \sqrt{33}} \\ (2):\cos\theta ={(0,1,0)\cdot \vec n\over |\vec n|}= {4\over \sqrt{33}}\\ (3):與(2)相同,\cos\theta={4\over \sqrt{33}} \\(4):\cos\theta ={(1,1,0)\cdot \vec n\over \sqrt 2\cdot |\vec n|} ={3\over \sqrt{66}} \\(5):\cos\theta ={(0,1,1)\cdot \vec n\over \sqrt 2|\vec n|}={8\over \sqrt{66}}},挑|\cos\theta| 最大的,故選\bbox[red,2pt]{(5)}$$
解答:$$每種壽司可以只分給甲、只分給乙、只分給丙、分給甲乙各1、分給乙丙各1、分給甲丙各1\\,共有六種分法,因此有6^{10}種組合,故選\bbox[red,2pt]{(3)}$$
解答:
$$本題相當於求兩圖形\cases{y=\sin 2x+\cos 2x\\ y=\sin x+1/2}的交點數量,且滿足0\le x\le 2\pi\\y=\sin 2x +\cos 2x = \sqrt 2(\cos 45^\circ \sin 2x+\cos 2x\sin 45^\circ)=\sqrt 2\sin(2x+45^\circ)\\,圖形為\cases{最大值為\sqrt 2\\最小值-\sqrt 2 \\ 週期為\pi};另一圖形y=\sin x+{1\over 2},圖形為\cases{最大值:3/2\\ 最小值:-1/2 \\週期為2\pi}\\ 兩圖形共有四個交點(見上圖),故選\bbox[red,2pt]{(4)}$$
二、多選題
解答:$$(1)\times: 甲牧場在第2年的牛數量多於第3年\\(2)\times: 10單位是最少數量,不是中位數\\(3) \bigcirc:甲牧場牛隻數量幾乎是水平線,標準差很小\\(4)\bigcirc: 非常接近\\ (5)\bigcirc:\cases{甲牧場牛數量接近水平, 而豬數量略增,相關係數為正值\\ 乙牧場牛數量逐年遞增, 而豬數量略為減少,相關係數為負值} \Rightarrow 甲牧場係數\gt 乙牧場\\,故選\bbox[red,2pt]{(345)}$$
解答:
$$(1)\times: \cases{(2,3)為頂點\\ y=f(x)開口向下} \Rightarrow y=f(x)=a(x-2)^2+3,a\lt 0 \Rightarrow y=f(-x)=a(-x-2)^2+3\\ \qquad = a(x+2)^2+3 開口仍向下\\(2)\bigcirc: y=g(x)為左上向下\Rightarrow y=g(-x)為左下右上\\(3)\times: 兩圖形\cases{y=g(x) \\ y=g(-x)}對稱y軸 \Rightarrow 對稱中心(2,-1) \Rightarrow (-2,-1)\\ (4)\times: y=g(x)的對稱中心(2,-1) \Rightarrow g(x)=b(x-2)^3 +c(x-2)-1 \\\qquad\Rightarrow f(x)+g(x)=b(x-2)^3+a(x-2)^2+c(x-2)+2 過(2,2),但非對稱中心\\(5) \bigcirc: y=f(x)開口向下,y=g(x)為左上右下,因此在x\lt 2恰有一交點\\,故選\bbox[red,2pt]{(25)}$$
解答:$$(1)\bigcirc: \overline{AC}-\overline{AB} \lt \overline{BC} \Rightarrow 3-2\lt a \Rightarrow a \gt 1\\(2)\times: 若為鈍角\triangle,只有\angle A或\angle B可能為鈍角,即\cases{\cos A={13-a^2\over 12} \lt 0\\ \cos B={a^2-5\over 4a}\lt 0} \Rightarrow \cases{a \gt\sqrt{13}\\ 0\lt a\lt \sqrt 5}\\ \qquad 例a=2,則B為鈍角;\\(3)\times: \overline{AC}\gt \overline{AB} \Rightarrow \angle B\gt \angle C(與a值無關)\\(4)\times: 正弦定理:{3\over \sin B}=2R= 2\sqrt 2\Rightarrow \sin B={3\over 2\sqrt 2} \gt 1矛盾\\(5)\bigcirc: {a\over \sin A} =2R=4042 \Rightarrow 存在a=4042\sin A\\,故選\bbox[red,2pt]{(15)}$$
解答:$$(1)\bigcirc: 個別號碼中獎機率都是({1\over 10})^3\\ (2)\times:({1\over 10})^3\ne {1\over 640}\\ (3)\times: \cases{1XX:XX=00-99,有100種可能\\ 6YY:YY=00-40,有40種可能}\Rightarrow 兩種中獎號碼的機率不同\\(4)\bigcirc: {360\over 1000} \times{360\over 1000} \times{640\over 1000} \approx 8.3\% \gt 5\%\\(5)\times: 第一輪有人中獎+第一輪沒人中且第二輪有人中+ 第一、二輪無人中且第三輪有人中獎的機率\\\qquad ={640\over 1000}+ {360\over 1000}\times {640\over 1000} +{360^2\over 1000^2}\times {640\over 1000}= 0.64(1+0.36+0.36^2) \approx 95.3\% \gt 93\%\\,故選\bbox[red,2pt]{(14)}$$
解答:$$(1)\bigcirc:O,A,D三點共線\Rightarrow \overrightarrow{OD}=m\overrightarrow{OA},m為常數\Rightarrow k\overrightarrow{OA}+ (2-k)\overrightarrow{OB} =m\overrightarrow{OA} \Rightarrow k=2 \\(2)\bigcirc:\overrightarrow{CD} =\overrightarrow{CO} +\overrightarrow{OD} =-(\overrightarrow{OA}+\overrightarrow{OB})+k\overrightarrow{OA}+ (2-k)\overrightarrow{OB} = (1-k)( \overrightarrow{AO}+ \overrightarrow{OB})\\ \qquad =(1-k)\overrightarrow{AB} \Rightarrow \overrightarrow{CD} \parallel \overrightarrow{AB}\\(3)\times: \overrightarrow{OC}=\overrightarrow{OA}+\overrightarrow{OB} =(a_1,a_2)+(b_1,b_2)=(a_1+b_1, a_2+b_2) \\\qquad \Rightarrow \triangle OAC={1\over 2}\begin{vmatrix} a_1 & a_2\\ a_1+b_1& a_2+b_2\end{vmatrix} ={1\over 2}\begin{vmatrix} a_1 & a_2\\ b_1& b_2\end{vmatrix}=1\\(4)\bigcirc: \overrightarrow{OD} =k\overrightarrow{OA}+ (2-k)\overrightarrow{OB} =(ka_1,ka_2)+ ((2-k)b_1,(2-k)b_2) = (ka_1+(2-k)b_1, ka_2+(2-k)b_2)\\ \qquad \Rightarrow \overrightarrow{AD}=((k-1)a_1+(2-k)b_1, (k-1)a_2+ (2-k)b_2)\\\qquad = (-k(b_1-a_1)-a_1+2b_1,-k(b_2-a_2)-a_2+2b_2) \Rightarrow \triangle ABD={1\over 2}\begin{vmatrix}\overrightarrow{AB}\\ \overrightarrow{AD} \end{vmatrix}\\ \qquad = {1\over 2}\begin{vmatrix}b_1-a_1 & b_2-a_2\\ -k(b_1-a_1)-a_1+2b_1&-k(b_2-a_2)-a_2+2b_2 \end{vmatrix} = {1\over 2}\begin{vmatrix}b_1-a_1 & b_2-a_2\\ -a_1+2b_1& -a_2+2b_2 \end{vmatrix}與k無關\\(5)\times: \triangle ACD={1\over 2}\begin{vmatrix}\overrightarrow{AC}\\ \overrightarrow{AD} \end{vmatrix}= {1\over 2}\begin{vmatrix}b_1 & b_2 \\ -k(b_1-a_1)-a_1+2b_1&-k(b_2-a_2)-a_2+2b_2 \end{vmatrix}與k相關\\,故選\bbox[red,2pt]{(124)}$$
解答:
解答:$$(1)\bigcirc: 個別號碼中獎機率都是({1\over 10})^3\\ (2)\times:({1\over 10})^3\ne {1\over 640}\\ (3)\times: \cases{1XX:XX=00-99,有100種可能\\ 6YY:YY=00-40,有40種可能}\Rightarrow 兩種中獎號碼的機率不同\\(4)\bigcirc: {360\over 1000} \times{360\over 1000} \times{640\over 1000} \approx 8.3\% \gt 5\%\\(5)\times: 第一輪有人中獎+第一輪沒人中且第二輪有人中+ 第一、二輪無人中且第三輪有人中獎的機率\\\qquad ={640\over 1000}+ {360\over 1000}\times {640\over 1000} +{360^2\over 1000^2}\times {640\over 1000}= 0.64(1+0.36+0.36^2) \approx 95.3\% \gt 93\%\\,故選\bbox[red,2pt]{(14)}$$
解答:$$(1)\bigcirc:O,A,D三點共線\Rightarrow \overrightarrow{OD}=m\overrightarrow{OA},m為常數\Rightarrow k\overrightarrow{OA}+ (2-k)\overrightarrow{OB} =m\overrightarrow{OA} \Rightarrow k=2 \\(2)\bigcirc:\overrightarrow{CD} =\overrightarrow{CO} +\overrightarrow{OD} =-(\overrightarrow{OA}+\overrightarrow{OB})+k\overrightarrow{OA}+ (2-k)\overrightarrow{OB} = (1-k)( \overrightarrow{AO}+ \overrightarrow{OB})\\ \qquad =(1-k)\overrightarrow{AB} \Rightarrow \overrightarrow{CD} \parallel \overrightarrow{AB}\\(3)\times: \overrightarrow{OC}=\overrightarrow{OA}+\overrightarrow{OB} =(a_1,a_2)+(b_1,b_2)=(a_1+b_1, a_2+b_2) \\\qquad \Rightarrow \triangle OAC={1\over 2}\begin{vmatrix} a_1 & a_2\\ a_1+b_1& a_2+b_2\end{vmatrix} ={1\over 2}\begin{vmatrix} a_1 & a_2\\ b_1& b_2\end{vmatrix}=1\\(4)\bigcirc: \overrightarrow{OD} =k\overrightarrow{OA}+ (2-k)\overrightarrow{OB} =(ka_1,ka_2)+ ((2-k)b_1,(2-k)b_2) = (ka_1+(2-k)b_1, ka_2+(2-k)b_2)\\ \qquad \Rightarrow \overrightarrow{AD}=((k-1)a_1+(2-k)b_1, (k-1)a_2+ (2-k)b_2)\\\qquad = (-k(b_1-a_1)-a_1+2b_1,-k(b_2-a_2)-a_2+2b_2) \Rightarrow \triangle ABD={1\over 2}\begin{vmatrix}\overrightarrow{AB}\\ \overrightarrow{AD} \end{vmatrix}\\ \qquad = {1\over 2}\begin{vmatrix}b_1-a_1 & b_2-a_2\\ -k(b_1-a_1)-a_1+2b_1&-k(b_2-a_2)-a_2+2b_2 \end{vmatrix} = {1\over 2}\begin{vmatrix}b_1-a_1 & b_2-a_2\\ -a_1+2b_1& -a_2+2b_2 \end{vmatrix}與k無關\\(5)\times: \triangle ACD={1\over 2}\begin{vmatrix}\overrightarrow{AC}\\ \overrightarrow{AD} \end{vmatrix}= {1\over 2}\begin{vmatrix}b_1 & b_2 \\ -k(b_1-a_1)-a_1+2b_1&-k(b_2-a_2)-a_2+2b_2 \end{vmatrix}與k相關\\,故選\bbox[red,2pt]{(124)}$$
解答:
$$L:{x-1/2\over 1} ={y-1/3\over 2}={z-1/4\over 3},若Q\in L,Q=(t+1/2,2t+1/3,3t+1/4),t\in \mathbb{R}\\ 先求L與EFGH平面的交集,即3t+{1\over 4}=1 \Rightarrow t={1\over 4} \Rightarrow Q=({3\over 4},{5\over 6},1)\in 立方體的頂面;\\再求L與ABCD平面的交集,即3t+{1\over 4}=0 \Rightarrow t=-{1\over 12} \Rightarrow Q=({5\over 12},{1\over 6},0)\in 立方體的底面;\\ 因此L與立方體交於頂面與底面,與四個側面無交集,故選\bbox[red,2pt]{(5)}$$
解答:$$\log_2 32=5 \Rightarrow 1000\sum_{k=0}^52^k=1000(1+2+4+8+16+32) =1000\times 63 =\bbox[red,2pt]{63}千元$$
解答:$${使用超過1年且為A廠生產的電池數量\over 使用超過1年的電池數量} ={0.4\times 0.9\over 0.4\times 0.9+0.6\times 0.75} ={0.36\over 0.81} =\bbox[red,2pt]{4\over 9}$$
解答:$$f(x)=x^2-3x+3 =(x-{3\over 2})^2+{3\over 4} \Rightarrow f(x)的最小值為=f({3\over 2})={3\over 4}\\ \Rightarrow y的最小值為a^{3/4} ={27\over 8} =({3\over 2})^3 \Rightarrow a^{1/4}={3\over 2} \Rightarrow a=({3\over 2})^4= \bbox[red, 2pt]{81\over 16}$$
解答:
解答:$$P在直線y=x+1上 \Rightarrow P(t,t+1) \Rightarrow T(t,t+1)=P'(at-bt-b,bt+at+a)\\ P'代入直線y=5x+13 \Rightarrow at+bt+a=5(at-bt-b)+13 \Rightarrow (4a -6b)t+(13-a-5b)=0\\ \Rightarrow \cases{4a-6b=0 \\ 13-a-5b=0} \Rightarrow \bbox[red,2pt]{\cases{a=3\\ b=2}}$$
解答:$$假設\cases{P(x_p,y_p)\\ Q(x_q,y_q)} \Rightarrow \cases{P'=T(P)=(ax_p-by_p,bx_p+ay_p) \\ Q'=T(Q)= (ax_q-by_q,bx_q+ay_q)} \\\Rightarrow \overline{P'Q'}= \sqrt{(a(x_p-x_q)-b(y_p-y_q))^2 +(b(x_p-x_q)+a(y_p-y_q))^2} \\ =\sqrt{a^2(x_p-x_q)^2 +b^2(y_p-y_q)^2 +b^2(x_p-x_q)^2+ a^2(y_p-y_q)^2}\\ =\sqrt{(a^2+b^2)(x_p-x_q)^2 +(a^2+b^2)(y_p-y_q)^2} =\sqrt{(a^2+b^2)((x_p-x_q)^2+ (y_p-y_q)^2)} \\ =\sqrt{a^2+b^2}\times \overline{PQ} \Rightarrow {\overline{P'Q'} \over \overline{PQ}} =\bbox[red,2pt]{\sqrt{a^2+b^2}}為一常數,此值為\sqrt{3^2+2^2}=\bbox[red, 2pt]{\sqrt{13}}$$
解答:$${使用超過1年且為A廠生產的電池數量\over 使用超過1年的電池數量} ={0.4\times 0.9\over 0.4\times 0.9+0.6\times 0.75} ={0.36\over 0.81} =\bbox[red,2pt]{4\over 9}$$
解答:$$f(x)=x^2-3x+3 =(x-{3\over 2})^2+{3\over 4} \Rightarrow f(x)的最小值為=f({3\over 2})={3\over 4}\\ \Rightarrow y的最小值為a^{3/4} ={27\over 8} =({3\over 2})^3 \Rightarrow a^{1/4}={3\over 2} \Rightarrow a=({3\over 2})^4= \bbox[red, 2pt]{81\over 16}$$
解答:
$$\Gamma:x^2+y^2-2x+6y+2=0 \Rightarrow (x-1)^2+ (y+3)^2=8 \Rightarrow \cases{圓心C(1,-3)\\ r=2\sqrt 2};\\ 令B(a,b),則\overline{CA} \times \overline{CB}= \sqrt 2\times \sqrt{(a-1)^2+ (b+3)^2}=r^2=8 \Rightarrow (a-1)^2+ (b+3)^2=(4\sqrt 2)^2 \\ \Rightarrow B在圓\Gamma':(x-1)^2+(y+3)^2=32上;又A、B、C在一直線上,且\overline{CA}: \overline{AB}=\sqrt 2:(4\sqrt 2-\sqrt 2) \\ =1:3 \Rightarrow A=(3C+B)\div 4 \Rightarrow \cases{2=(3+a)\div 4\\ -2=(-9+b)\div 4} \Rightarrow \cases{a=5\\ b=1} \Rightarrow B=\bbox[red,2pt]{(5,1)}$$
解答:$$假設四面體邊長為1,因此令\cases{A(0,1,1)\\ B(1,1,0)\\ C(1,0,1)\\ D(0,0,0)}\Rightarrow \cases{\overrightarrow{AB} =(1,0,-1)\\ \overrightarrow{AC} =(1,-1,0)} \Rightarrow \vec n=\overrightarrow{AB}\times \overrightarrow{AC} =(-1,-1,-1)\\ 由於\overrightarrow{AE}\cdot \overrightarrow{AB}=\overrightarrow{AE} \cdot \overrightarrow{AC}=0\Rightarrow \overrightarrow{AE}\parallel \vec n \Rightarrow E\in {x\over -1}={y-1\over -1}={z-1\over -1} (過A且方向向量為\vec n之直線)\\\Rightarrow E=(-t,-t+1,-t+1), t\lt 0(\because D,E在\triangle ABC異側) \Rightarrow \cases{\overrightarrow{AE}=(-t,-t,-t)\\ \overrightarrow{AD}=(0,-1,-1)} \\ \Rightarrow \cos \angle DAE ={\overrightarrow{AD}\cdot \overrightarrow{AE}\over |\overrightarrow{AD}|| \overrightarrow{AE}|} ={2t\over \sqrt 2\cdot \sqrt{3t^2}} =\bbox[red,2pt]{-{\sqrt 6\over 3}}$$
第貳部分、混合題或非選擇題
解答:$$T=\begin{bmatrix} a & -b\\ b& a\end{bmatrix} \Rightarrow T(0,1)=(-b,a) 代入直線y=5x+13 \Rightarrow a=-5b+13\\ \Rightarrow a+5b=13,故選\bbox[red,2pt]{(2)}$$解答:$$P在直線y=x+1上 \Rightarrow P(t,t+1) \Rightarrow T(t,t+1)=P'(at-bt-b,bt+at+a)\\ P'代入直線y=5x+13 \Rightarrow at+bt+a=5(at-bt-b)+13 \Rightarrow (4a -6b)t+(13-a-5b)=0\\ \Rightarrow \cases{4a-6b=0 \\ 13-a-5b=0} \Rightarrow \bbox[red,2pt]{\cases{a=3\\ b=2}}$$
解答:$$假設\cases{P(x_p,y_p)\\ Q(x_q,y_q)} \Rightarrow \cases{P'=T(P)=(ax_p-by_p,bx_p+ay_p) \\ Q'=T(Q)= (ax_q-by_q,bx_q+ay_q)} \\\Rightarrow \overline{P'Q'}= \sqrt{(a(x_p-x_q)-b(y_p-y_q))^2 +(b(x_p-x_q)+a(y_p-y_q))^2} \\ =\sqrt{a^2(x_p-x_q)^2 +b^2(y_p-y_q)^2 +b^2(x_p-x_q)^2+ a^2(y_p-y_q)^2}\\ =\sqrt{(a^2+b^2)(x_p-x_q)^2 +(a^2+b^2)(y_p-y_q)^2} =\sqrt{(a^2+b^2)((x_p-x_q)^2+ (y_p-y_q)^2)} \\ =\sqrt{a^2+b^2}\times \overline{PQ} \Rightarrow {\overline{P'Q'} \over \overline{PQ}} =\bbox[red,2pt]{\sqrt{a^2+b^2}}為一常數,此值為\sqrt{3^2+2^2}=\bbox[red, 2pt]{\sqrt{13}}$$
============== END =================

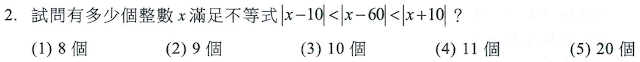






















實在不錯。
回覆刪除最後一題沒有寫到常數值
回覆刪除已補充, 謝謝!
刪除您好,是不是可以把此篇放進"大考中心學測及指考-數學科詳解目次"裡,比較好搜尋,謝謝
回覆刪除好的, 110試辦的數A/數B皆放置於目次中....
刪除