高雄區公立高級中等學校 112 學年度聯合招考轉學生
《 高 1 升高 2》《 數學》科試卷
一、 單一選擇題（ 60 分）
$$\bbox[cyan,2pt]{本題送分}$$
解答：$$序位不變，故選\bbox[red, 2pt]{(C)}$$
解答：$$\cases{A(2,2)\\ B(-1,7)} \Rightarrow \overleftrightarrow{AB}: 5x+3y=16 \Rightarrow C=\overleftrightarrow{AB} \cap L = (5,-3) \Rightarrow \cases{\overline{AC}= \sqrt{3^2+5^2}=\sqrt{34} \\ \overline{BC}=\sqrt{6^2+10^2} =2\sqrt{34}} \\ \Rightarrow \overline{AC}: \overline{BC}=1:2，故選\bbox[red, 2pt]{(A)}$$
解答：$$乙需連勝２局才獲勝，機率為{1\over 3}\times {1\over 3}={1\over 9}，因此甲獲勝的機率=1-{1\over 9}={8\over 9} \\ \Rightarrow 甲應分配3600\times {8\over 9}=3200，故選\bbox[red, 2pt]{(C)}$$
解答：$$C^2_2 +C^3_2 +\cdots +C^{19}_2 =\sum_{n=2}^{19} C^n_2 =\sum_{n=2}^{19} {n(n-1)\over 2} = {1\over 2}\sum_{n=2}^{19}(n^2-n) = {1\over 2}\sum_{n=1}^{19}(n^2-n) \\={1\over 2}\left( {19\cdot 20\cdot 39 \over 6}-{19\cdot 20\over 2} \right) =1140，故選\bbox[red, 2pt]{(D)}$$
解答：$$a-b=(\sqrt 3+\sqrt{17})-(\sqrt 5+\sqrt{15})，而\cases{(\sqrt 3+\sqrt{17})^2=20+2\sqrt{51} \\ (\sqrt 5+\sqrt{15})^2 =20+2\sqrt{75}} \Rightarrow a-b\lt 0 \Rightarrow a\lt b\\ a-c=(\sqrt 7+\sqrt{17}) -(\sqrt 5+\sqrt{19})，而\cases{(\sqrt 7+\sqrt{17})^2= 24+2\sqrt{139} \\ (\sqrt 5+\sqrt{19})^2= 24+2\sqrt{95}} \Rightarrow a\gt c \\ 因此c\lt a\lt b，故選\bbox[red, 2pt]{(B)}$$
解答：$$假設\cases{A(0,0)\\ B(1,-1)\\ C(m,n)} \Rightarrow \cases{若A為直角 \Rightarrow C在直線x=y上\Rightarrow m=n \\ 若B為直角\Rightarrow C在直線x-y=2上 \Rightarrow m=n+2} \\ \Rightarrow (m,n)=(1,1),(2,2),(3,3),(4,4), (5,5),(6,6),(3,1),(4,2),(5,3), (6,4)，共10點\\ 機率={10\over 36} ={5\over 18}，故選\bbox[red, 2pt]{(C)}$$
解答：$$\cases{a,b,c成等比\Rightarrow b^2=ac\\ a,b的等差中項為x \Rightarrow x=(a+b)/2\\ b,c的等差中項為y \Rightarrow y=(b+c)/2} \Rightarrow {a\over x}+ {c\over y} ={2a\over a+b}+{2c\over b+c} ={2a(b+c)+ 2c(a+b)\over (a+b)(b+c)} \\= {2(ab+ac+ac+bc)\over ab+ac+b^2+bc} ={2(ab+bc+ 2b^2) \over ab+bc+2b^2} =2，故選\bbox[red, 2pt]{(A)}$$
解答：$$\cases{a_1=2\\ a_{n+1}= 1/(1-a_n)} \Rightarrow \begin{array}{} a_1 & a_2 & a_3 & a_4 & a_5\\\hline 2 & -1 & 1/2 & 2 & -1\end{array} \Rightarrow 循環數=3 \Rightarrow a_{1000} =a_{333\cdot 3+1} =a_2=2\\，故選\bbox[red, 2pt]{(B)}$$
解答：$$假設\cases{小華擲出點數m\\ 小明擲出點數n}\Rightarrow \cases{小華獲勝的情形: (m,n)=(1-6,1), (2-6,2),(3-6,3),\\\qquad(4-6,4), (5-6,5)}\\ \Rightarrow 小華獲勝的情形有6+5+4+3+2=20種，故選\bbox[red, 2pt]{(A)}$$
解答：$$每個球有3種選擇，共有3^5=243種情形\\ 若A籃框沒有球，每個球有2種選擇，共有2^5=32種情形;\\同理B籃框沒有球或C籃框沒有球，也各有32種情形\\ 若A,B兩籃框皆無進球，只有1種情形；\\同理B,C兩籃框皆無進球或Ａ,C兩籃框皆無進球也各有1種情形\\ 因此恰有１籃框沒有球的情形3\times(32-2)=90，機率為{90\over 243} ={10\over 27}，故選\bbox[red, 2pt]{(D)}$$
解答：$$一票之差 \Rightarrow 小熊得5票，小豬得4票，代入公式：\\C^{5+4}_5-C^{4+5}_{5+1} =C^9_5-C^9_6=126-84=42，故選\bbox[red, 2pt]{(C)}$$
解答：$${20\times 10^{-7}+ 10^{-3} \over 20+1} ={2\times 10^{-6}+1000\times 10^{-6} \over 21} ={1002\over 21}\times 10^{-6} \approx 47.7\times 10^{-6} =4.77\times 10^{-5}\\ 又10^{-5} \lt 4.77\times 10^{-5} \lt 10^{-4} \Rightarrow ph值介於4,5之間，故選\bbox[red, 2pt]{(C)}$$
解答：
10. 小華、小明兩人各擲一顆公正的骰子，並約定如下：若小明只要丟出 6 點就算小明獲勝，小明丟出非 6 點且兩人同點數時小華獲勝，其餘的情形以點數大者獲勝，則小華獲勝的情形有幾種？
(A)20 (B)21 (C)22 (D)23
12. 學生會長選舉是動物國小每年最盛大的活動，今年的競爭尤為激烈，候選人小熊和小豬各自擁有高人氣。最終開票結果， 小熊以一票之差獲勝，若票數共 9 張，且小熊在唱票過程中始終不落後於小豬，則唱票過程有幾種可能？
(A) 14 (B) 21 (C) 42 (D) 84
13. 如果某溶液的 pH 值為 x，表示其中氫離子的莫耳濃度為每公升 \(10^{-x}\) 莫耳。請問：設純水的 pH 值為 7，若甲溶液的 pH 值為 3，則以甲溶液與 20 倍體積純水混和，則此混合溶液的 pH 值會介於哪兩個連續整數之間？
(A)2~3 (B) 3~4 (C) 4~5 (D) 5~6
14. 有一三角形廣場，其頂點處分別有 A,B,C 三盞路燈，位於該廣場垂心處有一座雕像。今若以 b 表示 A 燈與 C 燈之距離，則 A 燈與雕像之距離可用下列哪一個選項表示？$$(A) {b\cos A\over \sin B} \qquad (B) {b\cos A\over \cos B} \qquad (C) b\cos A\sin B \qquad (D) b\cos A\tan B $$
$$\cases{\overline{AE}= \overline{AC}\cos A= b\cos A \\ \overline{AE}= \overline{AP} \cos \angle EAP =\overline{AP} \cos (90^\circ-\angle B) =\overline{AP}\sin B} \\ \Rightarrow b\cos A= \overline{AP}\sin B \Rightarrow \overline{AP}={b\cos A\over \sin B}，故選\bbox[red, 2pt]{(A)}$$
解答：$$圓心至切線的距離即為圓半徑 \Rightarrow r={|3-4-9|\over \sqrt{3^2+4^2}} ={10\over 5}=2 \\ \Rightarrow 圓方程式: (x-1)^2+ (y+1)^2=2^2，故選\bbox[red, 2pt]{(B)}$$
解答：$$(A)\bigcirc:(\sqrt a+{1\over \sqrt a})=5 \Rightarrow a+2+{1\over a}=25 \Rightarrow a+{1\over a}=23 \\(B) \bigcirc:(a+{1\over a})^2= a^2+2+{1\over a^2}=23^2 \Rightarrow a^2+{1\over a^2} =527 \\(C) \bigcirc: (a+{1\over a})^3=a^3+{1\over a^3}+3(a+{1\over a}) =23^3 \Rightarrow a^3+{1\over a^3}=12098\\ \qquad (a^{3/2}+a^{-3/2})^2=a^3+2+a^{-3}= 12098+2=12100 \Rightarrow a^{3/2}+a^{-3/2}=\sqrt{12100}=110\\(D) \bigcirc: (a^{1/4}+a^{-1/4})^2= \sqrt a+2+{1\over \sqrt a} =5+2=7 \Rightarrow a^{1/4}+a^{-1/4}=\sqrt 7 \\(E)\bigcirc: (\sqrt a-{1\over \sqrt a})^2 = a+{1\over a}-2=23-2=21 \Rightarrow \sqrt a-{1\over \sqrt a}=\sqrt{21}\\，故選\bbox[red, 2pt]{(ABCDE)}$$
解答：$$假設原公里高度為x,原攝氏溫度y\\ (A)\bigcirc: 無論單位換算，高度越高溫度越低，因此r\lt 0且m\lt 0 \Rightarrow rm\gt 0 \\(B)\times:高度越高溫度越低 \Rightarrow r\lt 0 \\(C)\bigcirc: \cases{x'=0.6215x \\y'=1.8y+32} \Rightarrow 相關係數R={0.6215 \cdot 1.8 \over |0.6215 \cdot 1.8|} r= r \\(D)\times: R\lt 0 \Rightarrow M\lt 0 \\(E) \times:\sigma_{y'}/ \sigma{x'} \ne \sigma_y/ \sigma_x \Rightarrow m \ne M\\，故選\bbox[red, 2pt]{(AC)}$$
解答：$$假設L_1:x-y-9=0,L_2:x+2y=0,L_3 :3x-y-7=0\\(A) \bigcirc: \cases{A=L_1 \cap L_2 =(6,-3) \\ B=L_2 \cap L_3 = (2,-1)\\ C=L_1\cap L_3=(-1,-10)} \\(B) \bigcirc: \cases{\overline{AB}的中垂線: 2x-y=10\\ \overline{BC}的中垂線: x+36=-16} \Rightarrow 兩中垂線交點O=(2,-6) \Rightarrow 圓半徑r=\overline{OA}=5\\ \qquad 外接圓方程式: (x-2)^2+(y+6)^2=25 \Rightarrow x^2+y^2-4x+12y+15=0 \\ \qquad \Rightarrow \cases{a=-4\\ b=12 \\ c=15} \Rightarrow a+b=8\\ (C)\times: 2a-b=-8-12=-20\ne 20 \\(D) \bigcirc: 圓心O(2,-6) \\(E)\bigcirc: a^2+b^2-4c= 16+144-60=100\\，故選\bbox[red, 2pt]{(ABDE)}$$
解答：$$f(x)=(x^2-1)Q(x)+2x+1\\ (A)\times: f(0)=-Q(0)+1 不一定為1 \\(B) \bigcirc: f(1)=2+1=3 \\(C)\bigcirc: f(x)=2x+1= 0\cdot Q(x)+2x+1 \\(D)\times: f(-1)=-2+1=-1,若f(x)=4x^3+2x^2-3\Rightarrow f(-1)=-4+2-3=-5\ne -1 \\(E)\times: 若f(x)=4x^4+2x^3-34 \Rightarrow f(1)=6-34=-28 \ne 3\\，故選\bbox[red, 2pt]{(BC)}$$
解答：$$圖形左右對稱且上下對稱為零相關，故選\bbox[red, 2pt]{(BCE)}$$
解答：$$\sin \theta={12\over 13} \Rightarrow \cos \theta=\pm {5\over 13}\\ (A) \times: \cos(180^\circ+ \theta) =-\cos \theta =\mp {5\over 13} \\(B)\times: \sin(270^\circ+ \theta) = -\cos \theta =\mp {5\over 13} \\(C)\bigcirc: \cos(270^\circ-\theta) =-\sin\theta =-{12\over 13} \\(D) \times: \sin(180^\circ+\theta) =-\sin\theta=-{12\over 13} \\(E) \bigcirc: \cos(90^\circ-\theta)=\sin \theta={12\over 13}\\，故選\bbox[red, 2pt]{(CE)}$$
解答：$$(A) \times: \sin A={1\over 2} \Rightarrow \angle A=30^\circ 或150^\circ \\(B)\bigcirc: 假設{a\over \sin A}={b \over \sin B}={c \over \sin C}= k \Rightarrow \cases{\sin A=a/k\\ \sin B=b/k\\ \sin C=c/k} \Rightarrow \cases{\sin^2 A+\sin^2B= (a^2+b^2)/k^2\\ \sin^2 C=c^2/k^2} \\ \qquad 若\sin^2 A+\sin^2B =\sin^2 C \Rightarrow a^2+b^2=c^2 \Rightarrow \angle C=90^\circ \\(C)\bigcirc: \cos A\lt 0 \Rightarrow \angle A\gt 90^\circ \Rightarrow \angle A為鈍角 \\(D)\bigcirc: 三角形兩邊之和大於第三邊，即a+b\gt c \Rightarrow {a\over k}+{b\over k}\gt {c\over k} \\ \qquad \Rightarrow \sin A+\sin B\gt \sin C\\ (E)\bigcirc: 若\cases{\angle A=160^\circ\\ \angle B=\angle C=10^\circ} \Rightarrow \cases{\sin A\lt 1/2\\ \sin B=\sin C\lt 1/2}\\，故選\bbox[red, 2pt]{(BCDE)}$$
解答：$$(A)\times: 若\cases{a=5\\ b=1\\ c=-1} \Rightarrow \cases{|a+b|=6\\ |a-b|=4} \Rightarrow |a+b| \not \le |a-b| \\(B)\bigcirc: \cases{(a-c)^2=a^2+c^2-2ac\\ (a+c)^2 =a^2+c^2+2ac} \Rightarrow (a-c)^2 \ge (a+c)^2 (因為ac \lt 0) \\(C)\bigcirc: |a-2b| \le |a|+2|b| \le |a|+3|b| \\(D)\bigcirc: |a|\lt |c| \Rightarrow a+c\lt 0 \Rightarrow b+c\lt 0(因b\lt a) \\ (E)\times: |b| \gt |c| \Rightarrow b+c\gt 0 \Rightarrow a+c\gt 0，故選\bbox[red, 2pt]{(BCD)}$$
二、 多重選擇題（ 40 分）
17. 氣溫隨高度不同而改變，為了研究高度對氣溫的影響，經過實地測量得到的資料如下： (1,14)， (1.5,11)， (2,7.5)，(2.5,4)， (3,1.5)，其中測量單位分別為公里和攝氏溫度。將此筆資料的相關係數記為 r，以最小平方法決定氣溫對高度的迴歸直線斜率記為 m ， 現將單位轉換為哩（一公里約等於 0.6215 哩）及華氏溫度（攝氏 x 度等於華氏\({9\over 5}x+32\)度），若單位換算後資料的相關係數記為 R，以最小平方法決定的氣溫對高度的迴歸直線斜率記為 M，下列關係有哪些是正確的？
(A) rm > 0 (B)r > 0 (C)r = R (D)M > 0 (E)m = M
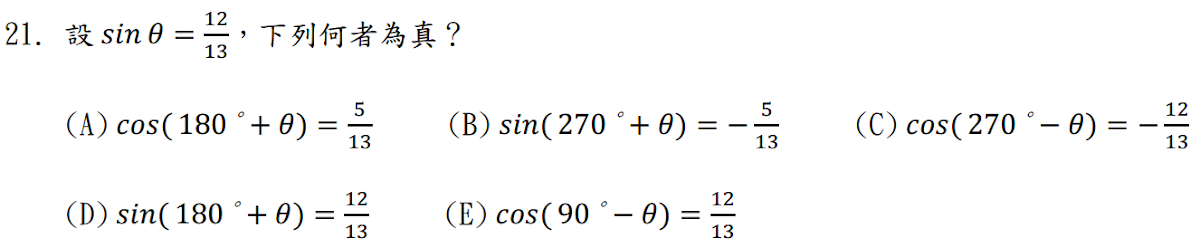
沒有留言:
張貼留言