97年第二次國民中學學生基本學力測驗
試題來源:師大心測中心
解:
一本x元,買了(x+2)本,共花了x(x+2)元
上述兩式相等,即 x(x+2)=500-17,故選(A)。
解:
BC=8⇒C=(9,-2+8)=(9, 6);DC=6⇒D=(9-6, 6)=(3, 6);
DE=4⇒E=(3, 6-4)=(3, 2);EF=2⇒F=(3+2, 2)=(5, 2),
DE=4⇒E=(3, 6-4)=(3, 2);EF=2⇒F=(3+2, 2)=(5, 2),
故選(B)。
解:
解:
0.20523-0.20252=0.00271=2.71×10-3,故選(A)。
解:
$${2\over 3}\times (1+{1\over 2})-{3\over 2}\div ({1\over 2}-1) ={2\over 3}\times {3\over 2}-{3\over 2}\div (-{1\over 2}) =1-{3\over 2} \times (-2) =1+3=4,故選\bbox[red, 2pt]{(A)}$$。
解:
解:
假設第4次的成績為a分,依題意:
(87+83+88+a)/4=(87+83+88)/3 +1
⇒3(87+83+88+a)=4(87+83+88)+12
⇒3a=(87+83+88)+12=270⇒a=90,故選(D)。
(87+83+88+a)/4=(87+83+88)/3 +1
⇒3(87+83+88+a)=4(87+83+88)+12
⇒3a=(87+83+88)+12=270⇒a=90,故選(D)。
(A) 8 (B) 9 (C) 12 (D) 18
解:
解:
同學總人數=1+6+4+x=11+x。
在成績1~15的次數為5%,即1/(11+x)=0.05,因此x=9。
y=x/(x+11)=9/20=45%,y=45。
z=5+30=35, u=5+30+20=55。故選(C)。
在成績1~15的次數為5%,即1/(11+x)=0.05,因此x=9。
y=x/(x+11)=9/20=45%,y=45。
z=5+30=35, u=5+30+20=55。故選(C)。
解:
該數列為一等差數列,公差為4,第1個數為3、第2個數為4...,即an=(n-1)×4+3。a15=(15-1)×4+3,a20=(20-1)×4+3。
a20-a15=19×4-14×4=5×4=20,故選(D)。
a20-a15=19×4-14×4=5×4=20,故選(D)。
解:
該設各袋皆有a個球,即(甲, 乙, 丙)=(a, a, a)。
從甲袋取出3球放入乙袋:(a, a, a)⇒(a-3, a+3, a)
再從乙袋取出5球放入丙袋:(a-3, a+3, a)⇒(a-3, a+3-5, a+5)
丙袋的球數為乙袋的2倍:a+5=2(a+3-5)=2(a-2)=2a-4⇒a=9⇒三袋共有3×9=27球,故選(B)。
從甲袋取出3球放入乙袋:(a, a, a)⇒(a-3, a+3, a)
再從乙袋取出5球放入丙袋:(a-3, a+3, a)⇒(a-3, a+3-5, a+5)
丙袋的球數為乙袋的2倍:a+5=2(a+3-5)=2(a-2)=2a-4⇒a=9⇒三袋共有3×9=27球,故選(B)。
解:
假設第n排的座位有an個,即an=30+(n-1)×2。
前n排的座位共有sn個,即sn=n(n-1)+30n。
前7排共有s7個座位,s7=7(7-1)+30×7=252=20×12+12。也就是前7排坐了1~12班的同學,再加上第13班12位同學。
第8排有a8=30+7×2=44個座位,即有8位第13班的同學及第14班全班(20位)及第15班44-8-20=16位同學坐在第8排,故選(C)。
前n排的座位共有sn個,即sn=n(n-1)+30n。
前7排共有s7個座位,s7=7(7-1)+30×7=252=20×12+12。也就是前7排坐了1~12班的同學,再加上第13班12位同學。
第8排有a8=30+7×2=44個座位,即有8位第13班的同學及第14班全班(20位)及第15班44-8-20=16位同學坐在第8排,故選(C)。
解:
甲:乙=7:3⇒乙=(3/10)(甲+乙)⇒乙=(3/20)(甲+乙+丙+丁)
丙:丁=5:9⇒丙=(5/14)(丙+丁)⇒丙=(5/28)(甲+乙+丙+丁)
乙:丙=(3/20):(5/28)=21:25,故選(C)。
丙:丁=5:9⇒丙=(5/14)(丙+丁)⇒丙=(5/28)(甲+乙+丙+丁)
乙:丙=(3/20):(5/28)=21:25,故選(C)。
解:
解:
△ABC為直角⇒AB2+BC2=AC2⇒AC=5
G為重心⇒D=(AC)/2=5/2
△ABC為直角且D為AC中心⇒AD=DC=BD=5/2
MG:BF=AG:AF=2:3⇒MG:(BC)/2=MG:3/2=2:3⇒MG=1
GN:EB=CG:CE=2:3⇒GN:2=2:3⇒GN=4/3
灰色面積=GN×MG=(4/3)×1=4/3,故選(D)。
△ABC為直角⇒AB2+BC2=AC2⇒AC=5
G為重心⇒D=(AC)/2=5/2
△ABC為直角且D為AC中心⇒AD=DC=BD=5/2
MG:BF=AG:AF=2:3⇒MG:(BC)/2=MG:3/2=2:3⇒MG=1
GN:EB=CG:CE=2:3⇒GN:2=2:3⇒GN=4/3
灰色面積=GN×MG=(4/3)×1=4/3,故選(D)。
五邊形內角總和=(5-2)×180=540⇒∠BCD=540-(103+110+113+115) = 99。
AB//A'C⇒∠ABC=∠A'CC'=115
∠BCD=∠BCA'+∠A'CD=99--------(1)
∠A'CC'=∠A'CD+∠DCC'=115-----(2)
∠BCC'=直線=∠BCA'+∠A'CD+∠DCC'=180---(3)
(1)+(2)-(3)⇒∠A'CD=99+115-180=34,故選(C)。
AB//A'C⇒∠ABC=∠A'CC'=115
∠BCD=∠BCA'+∠A'CD=99--------(1)
∠A'CC'=∠A'CD+∠DCC'=115-----(2)
∠BCC'=直線=∠BCA'+∠A'CD+∠DCC'=180---(3)
(1)+(2)-(3)⇒∠A'CD=99+115-180=34,故選(C)。
解:
解:
△ADH與△FGH相似⇒DH:HG=DA:FG=1:7⇒令DH=k, HG=7k⇒CD+DH+HG=7⇒1+k+7k=7⇒k=6/8=3/4,故選(B)。
解:
29. 下列各選項所呈現的資料,哪一個中位數最小?
(A) A到B的距離|a-b|與C到D的距離|2b|
(B) A到C的距離|b|與B到D的距離|a-2b|
(C) B到C的距離|a|與B到原點的距離|b|
(D) A到B的距離|a-b|與D到原點的距離|a-b|
故選(D)。
(B) A到C的距離|b|與B到D的距離|a-2b|
(C) B到C的距離|a|與B到原點的距離|b|
(D) A到B的距離|a-b|與D到原點的距離|a-b|
故選(D)。
29. 下列各選項所呈現的資料,哪一個中位數最小?
解:
解:
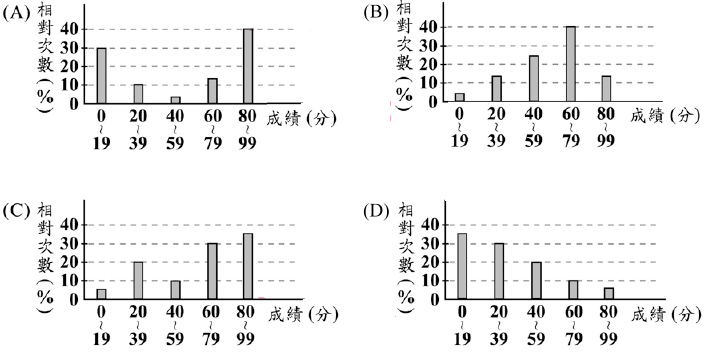
各選項的累積百分比分別為
(A) 30%, 40%, 45%, 60%, 100%
(B) 5%, 20%, 45%, 85%, 100%
(C) 5%, 25%, 35%, 65%, 100%
(D) 35%, 65%, 85%, 95%, 100%
在(D)中,成績低於39分的人數已過半了,故選(D)。
(A) 30%, 40%, 45%, 60%, 100%
(B) 5%, 20%, 45%, 85%, 100%
(C) 5%, 25%, 35%, 65%, 100%
(D) 35%, 65%, 85%, 95%, 100%
在(D)中,成績低於39分的人數已過半了,故選(D)。
解:
由於E為圓心,FE=EC=半徑=12
在直角三角形FEB中,斜邊FE是BE的2倍長,因此∠FEB=60°⇒∠FEC=120°⇒扇形EFC面積=12×12×π/3=48π
△FBE面積=6√3×6÷2=18√3
灰色面積=48π+18√3,故選(A)。
解:
72=12×6,12為其最大公因數,所以該數為2的倍數,也是3的倍數,也是4的倍數,不是8的倍數,也不是9的倍數。
2的倍數⇒b=0,2,4,6,8
3的倍數⇒1+a+b=3,6,9,12,15,18
先列出2的倍數,且為3的倍數,共有17個。在從中挑出4的倍數(末二位數是4的倍數),共有8個。再扣掉不是8的倍數,也不是9的倍數,只剩下132與156,其a+b=5及11,故選(B)。
2的倍數⇒b=0,2,4,6,8
3的倍數⇒1+a+b=3,6,9,12,15,18
先列出2的倍數,且為3的倍數,共有17個。在從中挑出4的倍數(末二位數是4的倍數),共有8個。再扣掉不是8的倍數,也不是9的倍數,只剩下132與156,其a+b=5及11,故選(B)。
解:
解:
對於兩人的做法,下列哪一個判斷是正確的?
(A) 兩人都正確 (B) 兩人都錯誤
(C) 甲正確,乙錯誤 (D) 甲錯誤,乙正確
解:
∠CAB=90°且I為內心⇒∠CAI=45°⇒A向右1再向上1在直線AI上,即(3,2)在直線AI上。
通過(2,1)及(3,2)的直線方程式為y=x-1⇒x=0時,y=-1,即(0,-1),故選(B)。
補充: 直線AI的斜率為1(因為角A為直角,且AI為角平分線),直線AI方程式可寫成y=x+b,加上過(2,1),可求得b=-1。
通過(2,1)及(3,2)的直線方程式為y=x-1⇒x=0時,y=-1,即(0,-1),故選(B)。
補充: 直線AI的斜率為1(因為角A為直角,且AI為角平分線),直線AI方程式可寫成y=x+b,加上過(2,1),可求得b=-1。
對於兩人的做法,下列哪一個判斷是正確的?
(A) 兩人都正確 (B) 兩人都錯誤
(C) 甲正確,乙錯誤 (D) 甲錯誤,乙正確
解:
--- END ---
解題僅供參考,其他歷年試題及詳解

























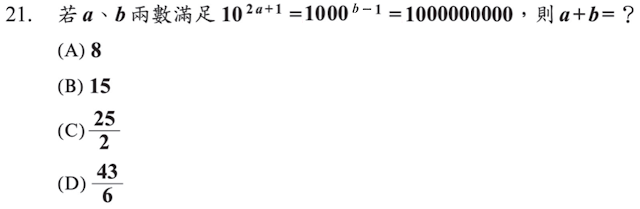




















想問一下33題
回覆刪除為何 「∠CAI=45°⇒A向右1再向上1在直線AI上,即(3,2)在直線AI上」?
角A是直角,AI直線平分角A,所以AI直線的斜率為1;所以A(2,1), (2+1,1+1), (2+2,1+2)...都在AI直線上。
刪除是想知道 為何AI直線斜率為1呢?
刪除AB是水平線, 角A是直角, AI是角平分線, 所以角IAB是45度,IA直線的斜率就是1啊........
刪除第五題和第四題的答案重複了
回覆刪除謝謝,已修訂
刪除