112年國中教育會考－數學詳解

112年國中教育會考

解答： $$(-3)^3= (-3) \times (-3) \times (-3)=9\times (-3)= -27，故選\bbox[red, 2pt]{(A)}$$

解答： $$x^2-36=x^2-6^2= (x+6)(x-6)，故選\bbox[red, 2pt]{(C)}$$

解答： $$乙的前面及後面都沒有積木，故選\bbox[red, 2pt]{(B)}$$

解答： $$\sqrt{135}= \sqrt{5\times 27} =\sqrt{5\times 3\times 3^2} =3\sqrt{5\times 3}=3\sqrt{15}，故選\bbox[red, 2pt]{(C)}$$

解答： $$x=-4 \Rightarrow y=-2\cdot (-4)-6=8-6=2，故選\bbox[red, 2pt]{(B)}$$

解答： $$\cases{a=-1= -{8\over 8}\\ b=-1{3\over 4}=-{7\over 4}=-{14\over 8} \\ c=-1{5\over 8}=-{13\over 8}} \Rightarrow a\gt c\gt b，故選\bbox[red, 2pt]{(A)}$$

解答： $$\cases{P在L的左邊\Rightarrow a\lt -5\\ P在M的上方\Rightarrow b\gt -3}，故選\bbox[red, 2pt]{(A)}$$

解答： $$\angle ADB= \angle ADC-\angle BDC=140^\circ-90^\circ=50^\circ\\ 又\overline{AD} \parallel \overline{BC} \Rightarrow \angle DBC=\angle ADB=50^\circ(內錯角相等)，故選\bbox[red, 2pt]{(C)}$$

解答： $$\cases{18=2\cdot 3^2\\ 216= 2^3\cdot 3^3} \Rightarrow 216=18 \cdot 2^2\cdot 3，而2^2\cdot 3有(2+1)\cdot (1+1)=6個因數\\ 因此有6個18的倍數，同時也是216的因數，即18,18\cdot 2,18\cdot 3,18\cdot 4,18\cdot 6,18\cdot 12，故選\bbox[red, 2pt]{(B)}$$

解答： $$a={11 +\sqrt{11^2-4\cdot 3\cdot(-1)}\over 2\cdot 3} ={11+\sqrt{133}\over 6}，故選\bbox[red, 2pt]{(D)}$$

解答： $$已知每毫升的咖啡因含量相同，假設為a毫克/毫升\\ 因此\cases{中杯360毫升有360a的咖啡因\\ 大杯480毫升有480a的咖啡因}，又\cases{中杯是黃標\\ 大杯是紅標}\Rightarrow \cases{100\lt 360a \le 200\\ 200\lt 480a} \\ \Rightarrow \cases{{10\over 36}\lt a\le {20\over 36} \\ {20\over 48}\lt a} \Rightarrow {20\over 48}\lt a\le {20\over 36}\\ 2杯中杯咖啡因含量為720\cdot {20\over 48}\lt 720a \le 720\cdot {20\over 36} \Rightarrow 300\lt 720a\le 400\\ \Rightarrow 超過我國建議量300，但低於歐盟建議量400，故選\bbox[red, 2pt]{(D)}$$

解答： $$\cases{動物系列買到喜歡的機率={2\over 6}\\ 汽車系列買到喜歡的機率={1\over 5}} \Rightarrow 同時買到喜歡的機率={2\over 6} \times {1\over 5}={1\over 15}，故選\bbox[red, 2pt]{(A)}$$

解答：

A

$$假設\cases{\angle 1=\angle CAB\\ \angle 2=\angle ACB\\ \angle 3=\angle AEB\\ \angle 4=\angle EAB}如上圖,\quad 在三角形中，大角對大邊\\ 直角三角形ABC：\cases{\angle ABC=90^\circ\\ \overline{BC}\gt \overline{AB}} \Rightarrow \cases{\angle 1+\angle 2 =90^\circ\\ \angle 1\gt 45^\circ \gt \angle 2}\\ 同理，直角三角形ABE：\cases{\angle ABE=90^\circ\\ \overline{AB}\gt \overline{BE}} \Rightarrow \cases{\angle 3+\angle 4=90^\circ \\ \angle 3\gt 45^\circ \gt \angle 4}\\ \angle FDE=\angle CAB=\angle 1 \gt \angle 2=\angle ACB\cdots(1)\\ \cases{\angle 2\lt 45^\circ\\ \angle 3\gt 45^\circ} \Rightarrow \angle AEB\gt \angle ACB \cdots(2)\\ 由(1)及(2)可得\angle ACB\lt \angle ACB, \angle AEB\gt \angle ACB，故選\bbox[red, 2pt]{(A)}$$

解答：

$$假設水平線與y軸交於E，且\overline{EA}=a，如上圖；\\ \cases{P的x坐標=a+{\overline{AC}\over 2}=a+{15\over 2} \\Q的x坐標=a+10+{\overline{BD}\over 2}=a+10+{11\over 2}} \\ \Rightarrow \overline{PQ}=a+10+{11\over 2}-(a+{15\over 2})=8，故選\bbox[red, 2pt]{(B)}$$

解答： $$在1，2之間、2，3之間、3，4之間及4，5之間，共四個間隔插入相同數量的一些數，\\ 就能維持等差數列；原來有5個數，每個間隔有a個數，共有5+4a個數；\\當a=7時，5+4a=33，故選\bbox[red, 2pt]{(D)}$$

解答： $$假設\cases{一片雞排a元\\ 一杯可樂b元} \Rightarrow 一份套裝餐a+b-40元 \Rightarrow 二份套餐2(a+b-40)\\ 促銷活動：a+2b=2(a+b-40)-10 \Rightarrow a=2a-90 \Rightarrow a=90，故選\bbox[red, 2pt]{(C)}$$

解答：

$$假設O為原點、A(1,3)則\triangle ABC外接圓半徑r=\overline{OA}=\sqrt{10}\\ 在方格紙上找B與C且\overline{OB}=\overline{OC}=\sqrt{10},只有(3,1),(-1,3)，\\其它符合條件的點不在此方格紙上，因此\overline{BC}=\sqrt{4^2+2^2} =\sqrt{20}，故選\bbox[red, 2pt]{(D)}$$

解答： $$\cases{在停車時段:08:00－12:00停了20-10=10小時，花費10\cdot 20=200元，收費100元\\ 在停車時段:20:00－08:00停了x-10小時，花費5\cdot(x-10)\le 5\cdot 4=20元,沒超過30元}\\ 因此停車費為100+5(x-10)=50+5x，故選\bbox[red, 2pt]{(B)}$$

解答：

$$假設D與D'對稱於\overline{AB}，則\stackrel{\large{\frown}}{D'B}= \stackrel{\large{\frown}}{BC}=35^\circ; 由於\overline{AC}為直徑，因此\stackrel{\large{\frown}}{AD'} +\stackrel{\large{ \frown}}{D'B}+ \stackrel{\large{ \frown}}{BC}=180^\circ\\ \Rightarrow \stackrel{\large {\frown}}{AD }=\stackrel{\large {\frown}}{AD'}=180^\circ-35^\circ-35^\circ=110^\circ，故選\bbox[red, 2pt]{(B)}$$

解答：

$$假設\cases{G為\overline{BD}中點\\ H為\overline{CD}中點 },並令\cases{\angle CFH=\angle HFD=a\\ \angle DEG=\angle GEB=b} \Rightarrow \cases{\angle C=\angle FDC=90^\circ-a\\ \angle B=\angle EDB=90^\circ-b} \\ \Rightarrow \cases{\angle 2= 180^\circ-\angle EDB-\angle FDC=180^\circ-(90^\circ-a)-(90^\circ-b)= a+b\\ \angle 4 = 180^\circ -\angle B-\angle C=180^\circ-(90^\circ-a)-(90^\circ-b)= a+b} \Rightarrow \angle 2=\angle 4\\ 又\cases{\angle 1=180^\circ-2b\\ \angle 3=180^\circ -2a}，由於三內角不相等，因此a\ne b，則\angle 1\ne \angle 2 \\，故選\bbox[red, 2pt]{(C)}$$

解答：

$$假設\cases{小維位於A點\\ 阿良位於B點}且\cases{小維每步a公分\\ 阿良每步b公分} ，交會點在C\\ 已知\overline{AC}=84a=70b，欲求\overline{BC}=60b=xa，其中的x值。\\ 84a=70b \Rightarrow b=1.2a \Rightarrow 60b=60\times 1.2a=72a \Rightarrow x=72，故選\bbox[red, 2pt]{(D)}$$

解答： $$正方形ABCD面積＝16 \Rightarrow 邊長＝4\Rightarrow \triangle BCG面積＝{1\over 2}\cdot \overline{BC}\cdot \overline{CD}=8\\\overline{FG} \parallel \overline{BC} \Rightarrow {\overline{FG}\over \overline{BC}} ={\overline{EG}\over \overline{EC}} ={\triangle EBG\over \triangle EBC} ={6\over 6+8}={3\over 7}，故選\bbox[red, 2pt]{(C)}$$

解答：

$$假設\cases{\overline{EP}=a\\ \overline{FP}=b} \Rightarrow \cases{\overline{FD}=\overline{AD}-\overline{AF}=8-a\\ \overline{BE}=\overline{AB}-\overline{AE}=6-b}\\ 又\angle EBP+ \angle BPE=90^\circ = \angle EBP+\angle FDP \Rightarrow \angle BPE=\angle FDP\\ 因此我們有\cases{\angle BEP=\angle DFP=90^\circ \\\angle BPE=\angle FDP} \Rightarrow \triangle BEP \sim \triangle PFD(AAA) \Rightarrow {\overline{BE}\over \overline{EP}}={\overline{FP} \over \overline{DF}} \\ \Rightarrow {6-b\over a}={8\over 8-a} \Rightarrow 3a+4b=24 \Rightarrow b={24-3a\over 4}\\ \overline{EF}^2 = a^2+b^2 = a^2+\left({24-3a\over 4} \right)^2 ={25\over 16}a^2-9a+36 ={25\over 16}(a-{72\over 25})^2+{576\over 25} \\ \Rightarrow \overline{EF}的最小值＝\sqrt{576\over 25}={24\over 5}，故選\bbox[red, 2pt]{(B)}$$

另解：

$$AEPF為一矩形，兩對角線  \overline{EF}=\overline{AP}；當\overline{AP}\bot \overline{BD}時，\overline{AP}最短，也就是\overline{EF}長度最小\\ \angle C=90^\circ \Rightarrow \overline{BD} =\sqrt{6^2+8^2}=10; 又\triangle ABD面積={1\over 2}\cdot \overline{AB}\cdot \overline{AD}= {1\over 2}\cdot \overline{BD}\cdot \overline{AP}\\ \Rightarrow 6\cdot 8=10\cdot \overline{AP} \Rightarrow \overline{AP}= {48\over 10}={24\over 5} \Rightarrow \overline{EF}的最小值＝{24\over 5}，故選\bbox[red, 2pt]{(B)}$$

解答：

$$在14\%至20\%區間內，水平距離最短的是韓國，見上圖，故選\bbox[red, 2pt]{(D)}$$

解答： $$2300\times(20\%-14\%)=138，故選\bbox[red, 2pt]{(A)}$$

解答： $$\mathbf{(1)}\;A廠牌：\cases{p={50\over 15000} \\ q={500\over 15000}} \Rightarrow {p\over q}={50\over 500}={1\over 10} \Rightarrow 疫苗效力=(1-{p\over q})\times 100\%=\bbox[red,2pt]{90\%}\\ \mathbf{(2)}\;只要{p \over q}\lt {1\over 10}，其疫苗效力就會大於A；\\例：B廠牌\cases{施打疫苗仍感染人數60\\ 施打安慰劑後感染人數800} 疫苗效力=(1-{60\over 800})\times 100 =92.5\%\gt 90\%，\\B廠施打疫苗仍感染人數高於A廠，但其疫苗效力高於A廠，因此答案為\bbox[red, 2pt]{不一定}$$

解答：

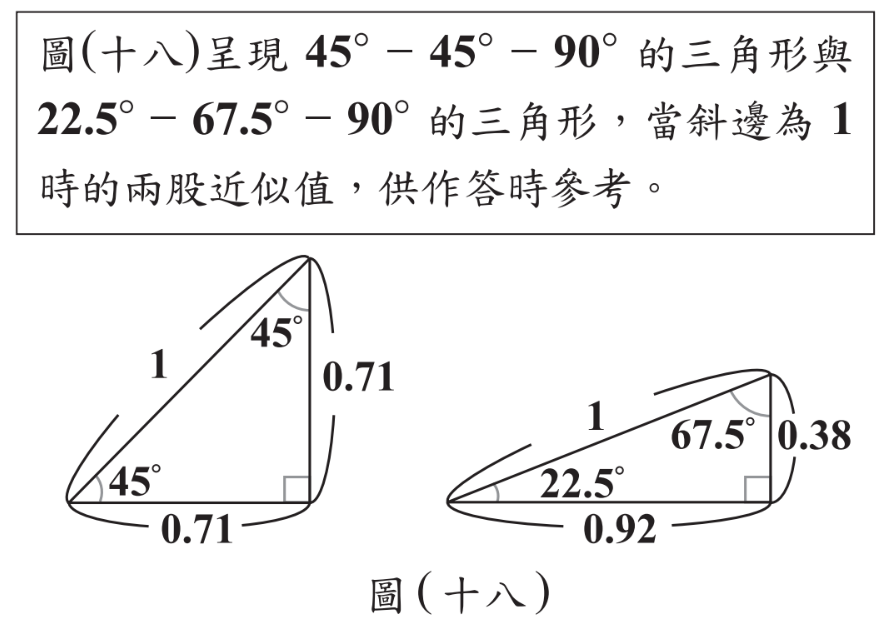
$$假設正八邊形外接圓半徑R，內切圓半徑r，見上圖；\\正八邊形\angle ABC=135^\circ \Rightarrow \angle OBA=\angle OAB={135\over 2}^\circ    \\又\overline{OQ}為\overline{AB}的中垂線\Rightarrow \angle AOQ=22.5^\circ，依圖(十八):{\overline{OQ}\over \overline{AQ}}={0.92\over 0.38} \Rightarrow {r\over 3}={0.92\over 0.38} \\\Rightarrow r= {3\times 0.92\over 0.38} \approx 7.26 \lt 8\Rightarrow \bbox[red,2pt]{套不住}$$

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝ END ＝＝＝＝＝＝＝＝＝＝＝＝＝＝

解題僅供參考，其他歷年試題及詳解