國立關西高級中學112學年度第1次教師甄選
一、多重選擇題(全對得6分,答錯一個選項得4分,答錯二個選項得2分,答錯三個選項以上不給分
解答:$$(A)\bigcirc: \cases{(11-1)^2+(0-1)^2=100+1=101 \\ (0-1)^2+(11-1)^2= 1+100=101} \Rightarrow \cases{(11,0)=x軸\cap \Gamma\\ (0,11)=y軸\cap \Gamma} \\(B)\times: 過圓心(1,1)的水平線L:y=1與\Gamma 交於(1-\sqrt{101},1),\\\qquad 而1-\sqrt{101}\lt 1-\sqrt{100}=-9\Rightarrow x軸最小的點是(1-\sqrt{101},1)\\ (C)\bigcirc: 圓心C與原點的連線L:y=x 與圓交於A,B(A在右上角,B在左下角)\\ \qquad \overline{OB}=直徑-半徑-\overline{OC}=2\sqrt{101}-\sqrt{101}-\sqrt 2=\sqrt{101}-\sqrt 2 \\(D)\times: 圓心不是原點\\ (E)\bigcirc: 只要還是圓就不會有xy項\\故選\bbox[red,2pt]{(ACE)}$$解答:$$(A)\bigcirc: \cases{7球排列數=7!/(2!2!3!)=210\\ 2黑球相鄰排列數=6!/(2!3!)=60} \Rightarrow 2黑球不相鄰排列數=210-60=150\\ \qquad \Rightarrow P(B)\gt P(A)\\(B) \bigcirc: 2黑球2白球的排列數=C^4_2=6,又在2黑球2白球的5個間隔中挑3個擺紅球有C^5_3=10種\\\qquad \Rightarrow P(C)=6\times 10/210=2/7 \\(C)\times: \cases{\#(C)=60\\ \#(A\cap C)=3C^4_3=12} \Rightarrow \#(B\cap C)=60-12=48 \\\qquad \Rightarrow \cases{P(C\mid A)=12/210\\ P(C\mid B)=48/210} \Rightarrow 2P(C\mid A)+5P(C\mid B)=2\cdot {12\over 60}+5\cdot {48\over 150}=2\not \gt 2 \\(D)\times: P(C\mid A)={12\over 60}=0.2 \not \gt 0.2\\(E) \bigcirc: P(C\mid B)={48\over 150}=0.32\gt 0.3\\ 故選\bbox[red, 2pt]{(ABE)}$$
解答:$$(A)\bigcirc:轉軸角度\phi \Rightarrow \cot 2\phi={5-8\over 4}=-{3\over 4} \Rightarrow \tan 2\phi=-{4\over 3} \Rightarrow \tan 2\theta={4\over 3} \\(B)\times: \tan 2\theta={4\over 2} \Rightarrow \cos 2\theta={3\over 5}\ne -{3\over 5}\\ (C) \times:\cases{\sin 2\theta=4/5\\ \cos 2\theta=3/5} \Rightarrow \cases{\sin \theta=1/\sqrt 5\\ \cos \theta=2/\sqrt 5} \Rightarrow 旋轉矩陣R =\begin{bmatrix}\cos\theta & -\sin \theta \\\sin \theta & \cos \theta \end{bmatrix} \\ \qquad \Rightarrow \begin{bmatrix}x' \\y' \end{bmatrix} =R\begin{bmatrix}x \\y \end{bmatrix} \Rightarrow \begin{bmatrix}x \\y \end{bmatrix}= R^{-1} \begin{bmatrix}x' \\y' \end{bmatrix}= \begin{bmatrix} \cos \theta & \sin \theta \\-\sin \theta & \cos \theta \end{bmatrix} \begin{bmatrix}x' \\y' \end{bmatrix}= \begin{bmatrix}(2x'+y')/\sqrt 5 \\(-x'+2y')/\sqrt 5 \end{bmatrix}\\ \qquad \Rightarrow 4x'^2+9y'^2=36 \Rightarrow {x'^2\over 9}+{y'^2\over 4}=1 \Rightarrow \cases{長軸長=2a=6\\ 短軸長=2b=4} \\(D) \bigcirc:橢圓面積=ab\pi= 3\cdot 2\cdot \pi=6\pi \\(E)\times: 正焦弦長={2b^2\over a}={8\over 3} \ne{4\over 3}\\ 故選\bbox[red, 2pt]{(AD)}$$
解答:$$(A)\bigcirc: \int_0^a f(t)\,dt =\left. \left[ F(t) \right] \right|_0^a =F(a)-F(0)\\ (B) \bigcirc: 令F(x)=xQ(x)+c \Rightarrow F'(x)=f(x)= Q(x)+xQ'(x)\\ \qquad \Rightarrow f(0)=Q(0)\\ (C)\times: 假設f(x)=x+2 \Rightarrow F(x)=\int f(x)\,dx ={1\over 2}x^2+2x+C \\\qquad \Rightarrow F(x)-F(0)={1\over 2}x^2+2x 不能被(x+2)^2整除\\ (D)\times: 假設F(x)=x^2,滿足F(x)\ge {x^2\over 2},但f(x)=F'(x)=2x \lt x, \forall x\lt 0 \\(E)\times: 取f(x)=\begin{cases}x & 0\lt x \le 1\\x^2 & x > 1\end{cases} \Rightarrow F(x)=\begin{cases}x^2/2 & 0\lt x \le 1\\x^3/3 & x >1\end{cases} \\ \qquad \Rightarrow \cases{F(1.2)=0.576\\ 1.2^2/2=0.72} \Rightarrow 當x=1.2時, F(x)\lt {1\over 2}x^2\\ 故選\bbox[red, 2pt]{(AB)}$$
二、填充題(每題5分)
解答:$$\left(1+{1\over 2}+ {1\over 2^2}+{1\over 2^3}+\cdots \right)\left(1+{1\over 3}+ {1\over 3^2}+{1\over 3^3}+\cdots \right)\left( 1+{1\over 5}+ {1\over 5^2}+{1\over 5^3}+\cdots \right)\\ \qquad \left(1+{1\over 7}+ {1\over 7^2}+{1\over 7^3}+\cdots \right) = 2\times {3\over 2}\times {5\over 4}\times {7\over 6} = \bbox[red, 2pt]{35\over 8}$$解答:$$|z|=1 \Rightarrow z=\cos \theta+i\sin \theta \Rightarrow z^2-z+2 =(\cos\theta+ i\sin \theta)^2-(\cos \theta+i\sin \theta)+2 \\=\cos 2\theta-\cos \theta+2+ (\sin 2\theta-\sin \theta)i\\ \Rightarrow |z^2-z+2|^2 =( \cos 2\theta-\cos \theta+2)^2+ (\sin 2\theta-\sin \theta)^2 =8\cos^2\theta-6\cos \theta +2\\ \Rightarrow 當\cos \theta={3\over 8}時,|z^2-z+2|有最小值\sqrt{7\over 8}= \bbox[red, 2pt]{\sqrt{14}\over 4}$$
解答:
$$令\cases{A(0,0)\\ B(8,0)\\ C(x,y)},再由\cases{\overline{AC}=9\\ \overline{BC}=7} \Rightarrow \cases{x^2+y^2=81\\ (x-8)^2+y^2=49} \Rightarrow C(6,3\sqrt 5) \\\Rightarrow L_1=\overleftrightarrow{AC}:y={\sqrt 5\over 2}x,取垂足P(a, \sqrt 5a/2),由\overrightarrow{AC}\cdot \overrightarrow{BP}=0 \Rightarrow a={32\over 9} \Rightarrow P({32\over 9},{16\over 9}\sqrt 5)\\ \Rightarrow L_2=\overleftrightarrow{BP}: 2\sqrt 5x+5y=16\sqrt 5 \Rightarrow L_2與\overline{AB}的中垂線交於Q(4,{8\sqrt 5\over 5})\\ 因此我們有\cases{\overrightarrow{AQ}=(4,{8\sqrt 5\over 5}) \\ \overrightarrow{AB}=(8,0)\\ \overrightarrow{AC}=(6,3\sqrt 5)},再由\overrightarrow{AQ} =x\overrightarrow{AB}+ y\overrightarrow{AC} \Rightarrow \bbox[red,2pt]{\cases{x=1/10\\ y=8/15}}$$
解答:$$x=1 \Rightarrow 1\cdot f(1)=3-2+4+0=5 \Rightarrow f(1)=5\\ {d\over dx}(xf(x))= f(x)+xf'(x)= 12x^3-6x^2+8x+ f(x) \Rightarrow f'(x)=12x^2-6x+8\\ \Rightarrow f(x)=4x^3-3x^2+8x+C,再由f(1)=5\Rightarrow 4-3+8+C=5\Rightarrow C=-4\\ \Rightarrow \bbox[red,2pt]{f(x)=4x^3-3x^2+8x-4}$$
解答:$$$$
解答:
解答:$$x=1 \Rightarrow 1\cdot f(1)=3-2+4+0=5 \Rightarrow f(1)=5\\ {d\over dx}(xf(x))= f(x)+xf'(x)= 12x^3-6x^2+8x+ f(x) \Rightarrow f'(x)=12x^2-6x+8\\ \Rightarrow f(x)=4x^3-3x^2+8x+C,再由f(1)=5\Rightarrow 4-3+8+C=5\Rightarrow C=-4\\ \Rightarrow \bbox[red,2pt]{f(x)=4x^3-3x^2+8x-4}$$
解答:$$$$
解答:
$$\cases{\angle CDB=\angle CAE(對同弧)=\angle 1\\ \angle E=\angle E} \Rightarrow \triangle ACE \sim \triangle DBE (AAA)\\ 又\overline{CD}=\overline{CB} \Rightarrow \angle CDB=\angle CBD=\angle CAD=\angle 2\\ 對同弧的\angle CDB=\angle CAB \Rightarrow \angle 1=\angle 2 \Rightarrow \triangle CDB\sim \triangle CAE (AAA)\\ 因此\triangle CAB\sim \triangle BDE \sim \triangle CDB \Rightarrow {\overline{BC}\over \overline{BD}} ={\overline{BE} \over \overline{DE}} \Rightarrow {ak\over 30k} ={30k\over ak+11k} \\ \Rightarrow a^2+11a-900=0 \Rightarrow (a-25)(a+36)=0 \Rightarrow a=25 \\\Rightarrow \overline{BC}: \overline{CD}: \overline{BD}= 25:25:30=5:5:6 \Rightarrow \cos BCD= {5^2+5^2-6^2\over 2\cdot 5\cdot 5} ={7\over 25} \\ \Rightarrow \sin \angle BCD= {24\over 25} \Rightarrow {\overline{BD}\over \sin \angle BCD}=2 \Rightarrow \overline{BD}=2\cdot {24\over 25} =\bbox[red, 2pt]{48\over 25}$$
解答:$$a,b,c為x^3-5x^2-3x+7=0的三根\Rightarrow \cases{a+b+c=5\\ ab+bc+ ca=-3\\ abc= -7} \\ \Rightarrow \begin{vmatrix}a-b-c &2a & 2a\\2b & b-c-a & 2b\\ 2c & 2c & c-a-b \end{vmatrix} = \begin{vmatrix}2a-5 &2a & 2a\\2b & 2b-5 & 2b\\ 2c & 2c & 2c-5 \end{vmatrix}\\ = \begin{vmatrix} 2(a+b+c)-5 &2(a+b+c)-5 & 2(a+b+c)-5 \\2b & 2b-5 & 2b\\ 2c & 2c & 2c-5 \end{vmatrix}= \begin{vmatrix} 5 & 5 & 5 \\2b & 2b-5 & 2b\\ 2c & 2c & 2c-5 \end{vmatrix}\\ =5\begin{vmatrix} 1 & 1 & 1 \\2b & 2b-5 & 2b\\ 2c & 2c & 2c-5 \end{vmatrix}= 5\begin{vmatrix} 1 & 1 & 1 \\0 & -5 & 0\\ 0 & 0 & -5 \end{vmatrix} = 5\cdot 25= \bbox[red,2pt]{125}$$
解答:$$$$
解答:$$將17個字分分成4組:\cases{A:\{ a,d,e,\ell ,o,s,u,z\} \\B:\{ i,i,i,i\} \\C:\{ n,n\} \\D:\{ t,t,t\} }\\ 四個字母取法如下表,合計共\bbox[red,2pt]{9539}種$$
解答:$$a,b,c為x^3-5x^2-3x+7=0的三根\Rightarrow \cases{a+b+c=5\\ ab+bc+ ca=-3\\ abc= -7} \\ \Rightarrow \begin{vmatrix}a-b-c &2a & 2a\\2b & b-c-a & 2b\\ 2c & 2c & c-a-b \end{vmatrix} = \begin{vmatrix}2a-5 &2a & 2a\\2b & 2b-5 & 2b\\ 2c & 2c & 2c-5 \end{vmatrix}\\ = \begin{vmatrix} 2(a+b+c)-5 &2(a+b+c)-5 & 2(a+b+c)-5 \\2b & 2b-5 & 2b\\ 2c & 2c & 2c-5 \end{vmatrix}= \begin{vmatrix} 5 & 5 & 5 \\2b & 2b-5 & 2b\\ 2c & 2c & 2c-5 \end{vmatrix}\\ =5\begin{vmatrix} 1 & 1 & 1 \\2b & 2b-5 & 2b\\ 2c & 2c & 2c-5 \end{vmatrix}= 5\begin{vmatrix} 1 & 1 & 1 \\0 & -5 & 0\\ 0 & 0 & -5 \end{vmatrix} = 5\cdot 25= \bbox[red,2pt]{125}$$
解答:$$$$
解答:$$將17個字分分成4組:\cases{A:\{ a,d,e,\ell ,o,s,u,z\} \\B:\{ i,i,i,i\} \\C:\{ n,n\} \\D:\{ t,t,t\} }\\ 四個字母取法如下表,合計共\bbox[red,2pt]{9539}種$$
$$\cos \angle PAB={15^2+35^2-25^2\over 2\cdot 15\cdot 35} ={11\over 14} \Rightarrow \sin \angle PAB={5\sqrt 3\over 14}\\ 又\cos \angle PAC= \cos (60^\circ-\angle PAB) = \cos 60^\circ \cos \angle PAB+ \sin60^\circ \sin \angle PAB \\={1\over 2}\cdot {11\over 14} +{\sqrt 3\over 2}\cdot {5\sqrt 3\over 14}={13\over 14} ={15^2+56^2-\overline{PC}^2\over 2\cdot 15\cdot 56 } \Rightarrow \overline{PC}=\bbox[red, 2pt]{\sqrt{1801}}$$

















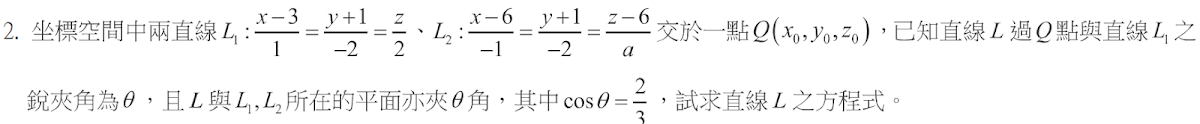




沒有留言:
張貼留言