112 學年度科技校院四年制與專科學校二年制
統 一 入 學 測 驗-數學(B)
解答:$$f(x)= (2x^2-3)^5 +3(x-1)^2 \Rightarrow f(1)= (-1)^5=-1, 故選\bbox[red, 2pt]{(B)}$$
解答:$$判別式\lt 0 \Rightarrow k^2-12h\lt 0\\ (A)\times:(-4)^2-12\cdot 1=4\gt 0 \\(B)\times: 12^2-12\cdot 12=0 \not \lt 0\\ (C)\times: 5^2-12\cdot 2=1\gt 0 \\(D)\bigcirc: 10^2-12\cdot 9=-9 \lt 0, 故選\bbox[red, 2pt]{(D)}$$
解答:$$L_1通過第一,三象限 \Rightarrow m_1\gt 0,又L_1\bot L_2 \Rightarrow m_1m_2 =-1 \Rightarrow m_2\lt 0, 故選\bbox[red, 2pt]{(D)}$$
解答:
$$\cases{a/2=-2\\ b/2=3} \Rightarrow \cases{a=-4\\ b=6} \Rightarrow f(x)={6\over 4}x+6 \Rightarrow f(2)=9 \\ \Rightarrow a+b+f(2)=-4+6+9=11, 故選\bbox[red, 2pt]{(A)}$$
解答:
$$錯誤的圓方程式:(x-1)^2+(y-2)^2=2^2 \xrightarrow{x,y互換}(x-2)^2+(y-1)^2=2^2\\ \Rightarrow x^2+y^2-4x-2y+1=0, 故選\bbox[red, 2pt]{(D)}$$
解答:
$$|\vec u|=|\vec w| \Rightarrow \vec u+\vec w是\vec u與\vec w夾角的角平分向量 \Rightarrow \vec u+\vec w與\vec u的夾角=75^\circ = \vec u+\vec w與\vec w的夾角\\ \Rightarrow -(\vec u+\vec w)與\vec w的夾角為180^\circ-75^\circ =105^\circ, 故選\bbox[red, 2pt]{(C)}$$
解答:
$$({1\over 2}+{1\over 2^2}x)+({1\over 2^2}+{1\over 2^3}x)+({1\over 2^3}+{1\over 2^4}x)+({1\over 2^4}+{1\over 2^5}x)+({1\over 2^5}+{1\over 2^6}x) \\ =({1\over 2}+{1\over 2^2}+\cdots+{1\over 2^5}) +({1\over 2^2}+{1\over 2^3}+ \cdots +{1\over 2^6})x \\={{1\over 2}-{1\over 2^6} \over 1-{1\over 2}} +{{1\over 2^2}-{1\over 2^7}\over 1-{1\over 2}}x={2^5-1\over 2^5}+{2^5-1\over 2^6}x \gt 0 \Rightarrow 2+x\gt 0 \Rightarrow x\gt -2, 故選\bbox[red, 2pt]{(D)}$$
解答:
$$ax+4y+k=0的斜率=-{a\over 4} ={1\over 2} \Rightarrow a=-2\\ 又(0,0)至L的距離={k\over \sqrt{a^2+16}}={k\over \sqrt{(-2)^2+16}} =\sqrt 5 \\ \Rightarrow k= \sqrt{20}\cdot \sqrt 5=10 \Rightarrow a+k=-2+10=8, 故選\bbox[red, 2pt]{(B)}$$
解答:
$$f(x)=(x+2)(x-7)p(x)+ax+3\\ (x-7)為f(x)的因式\Rightarrow f(7)=7a+3=0 \Rightarrow a=-{3\over 7} \\ \Rightarrow f(x)(x+2)(x-7)p(x)-{3\over 7}x+3 \Rightarrow f(-2)=-{3\over 7}\cdot (-2)+3 = {27\over 7}, 故選\bbox[red, 2pt]{(A)}$$
解答:
$$開口向下\Rightarrow n^2-n-12 \lt 0 \Rightarrow (n-4)(n+3)\lt 0 \Rightarrow -3\lt n\lt 4 \\ \Rightarrow n=-2,-1,0,1,2,3,共六個整數解, 故選\bbox[red, 2pt]{(C)}$$
解答:
$$f(x)=g(x) \Rightarrow \cases{2a-b=3\\ a=1} \Rightarrow b=-1 \Rightarrow Q(x)=x-1\\ 因此{x\over Q(x)}+{5\over x-2} ={x\over x-1}+{5\over x-2} ={x^2+3x-5\over (x-1)(x-2)} ={-1\over (x-2)Q(x)} \\ \Rightarrow x^2+3x-5=-1 \Rightarrow (x+4)(x-1)=0 \Rightarrow x=-4(x=1違反分母不為0) \\ \Rightarrow a^2+b^2+c^2 = 1+1+16=18, 故選\bbox[red, 2pt]{(C)}$$
解答:
解答:
$$\cases{\cos 39^\circ \tan 39^\circ = \sin 39^\circ \\ \sin129^\circ \tan 141^\circ = \sin 51^\circ\cdot (-{\sin 39^\circ\over \cos 39^\circ }) = \cos 39^\circ\cdot (-{\sin 39^\circ\over \cos 39^\circ }) =-\sin 39^\circ} \\ \Rightarrow \cos 39^\circ \tan 39^\circ+\sin129^\circ \tan 141^\circ=0 \\\Rightarrow 原式= \sin 30^\circ \tan 45^\circ \cos60^\circ ={1\over 2}\cdot 1\cdot {1\over 2} ={1\over 4}, 故選\bbox[red, 2pt]{(A)}$$
解答:
$$第n週的訓練長度=8+(n-1)\cdot 3\ge 42.195 \Rightarrow 3(n-1)\ge 34.195 \\ \Rightarrow n-1 \ge 11.398 \Rightarrow n\ge 12.198 \Rightarrow n=13, 故選\bbox[red, 2pt]{(B)}$$
解答:
$$依題意\cases{\vec u\cdot (1,3)=x+3y\le 14\\ \vec u\cdot (2,-1)=2x-y \le 14},求\vec u\cdot (1,1)=x+y的最大值\\ 兩直線\cases{x+3y=14\\ 2x-y=14} 交點為(8,2) \Rightarrow 8+2=10, 故選\bbox[red, 2pt]{(C)}$$
解答:
$$\cos \angle AED =\cos 120^\circ ={25^2+ 25^2 -\overline{AD}^2 \over 2\cdot 25 \cdot 25} \Rightarrow -{1\over 2}={1250-\overline{AD}^2 \over 1250} \\ \Rightarrow \overline{AD}^2= 1875 \Rightarrow \overline{AD}=25\sqrt 3 \Rightarrow ABCD面積=25\sqrt 3\times 18=450\sqrt 3, 故選\bbox[red, 2pt]{(C)}$$
解答:
$$37\log_{10} x+31 \gt 70 \Rightarrow \log_{10}x \gt {70-31\over 37}\approx 1.05\\ (A) x=9 \Rightarrow \log_{10}9 =2\times 0.4771\lt 1\\ (B)x=10 \Rightarrow \log_{10} 10=1 \lt 1.05\\ (C) x=12 \Rightarrow \log_{10}12 =2\log_{10}2+ \log_{10}3=2\cdot 0.301+ 0.4771=1.0791\\ (D)15\gt 12 \Rightarrow 12比較接近\\, 故選\bbox[red, 2pt]{(C)}$$
解答:
$$\cases{小楓:{50+40\over 100+200} ={90\over 300} \\小道: {90+15\over 200+100} ={105\over 300}} \Rightarrow 小道比較高, 故選\bbox[red, 2pt]{(A)}$$
解答:
$$(A)\times: 200\times 1900+ 100\times 1400=52萬\\(B) \bigcirc:200\times 1700+100\times 1600 = 50萬 \\(C)\times: 200\times 1800+ 100\times 1700=53萬 \\(D)\times: 200\times 1800+100\times 1500 = 51萬\\, 故選\bbox[red, 2pt]{(B)}$$
解答:
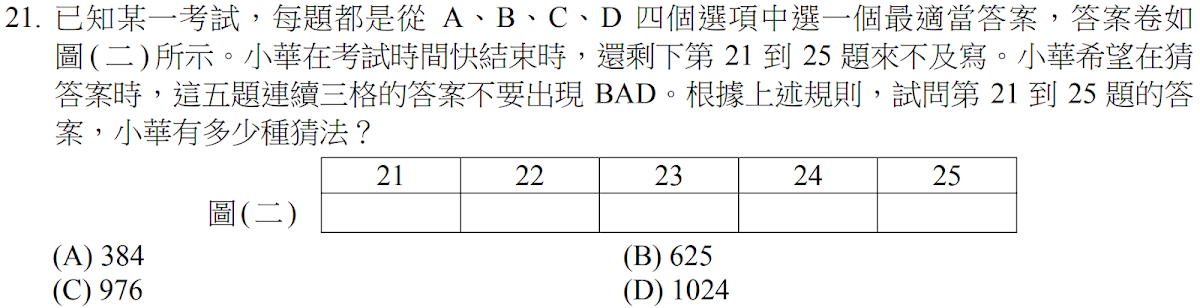
$$\cases{BAD\bigcirc \bigcirc:有4\times 4=16種 \\ \bigcirc BAD \bigcirc:有4\times 4=16種 \\ \bigcirc \bigcirc BAD :有4\times 4=16種 } \Rightarrow 共有4^5-16-16-16= 976種, 故選\bbox[red, 2pt]{(C)}$$
解答:
$$\cases{A:y=4\sin(2\pi t/11)+16 \Rightarrow \cases{最大值=4+16=20\\ 最小值=-4+16=12}\\ B:y=-5\cos(2\pi t/13)+17 \Rightarrow \cases{最大值=5+17=22\\ 最小值=-5+17=12}}, 故選\bbox[red, 2pt]{(A)}$$
解答:
$$(A)\times: y(2100)={600000 \over 1+2 \times 2.7^{-0.78}},分母\gt 1 \Rightarrow y(2100)\lt 60萬\\ (B)\bigcirc: y(2022) ={60萬\over 1+2}=20萬\\ (C)\times: x\gt 2022 \Rightarrow f(x)遞增 \Rightarrow f(2070)\gt f(2060)\\ (D)\times: 理由同(C),f(2080) \lt f(2090)\\, 故選\bbox[red, 2pt]{(B)}$$
解答:
$$假設有a間男廁被改建, 改建後a+4 \ge 3(4-a) \Rightarrow a=3,2\\ \cases{a=3 有C^4_3=4種選擇\\ a=2 有C^4_2= 6種選擇} \Rightarrow a=2的機率是{6\over 6+4}={3\over 5}, 故選\bbox[red, 2pt]{(D)}$$
解答:
$$假設涼亭至橋面高度h, 橋終點至山腳距離a, 如上圖\\ h=(870+a)\tan 30^\circ = a\tan 60^\circ \Rightarrow (870+a)\cdot {1\over \sqrt 3}=\sqrt 3a \Rightarrow a=435 \\ \Rightarrow h=435\sqrt 3 \Rightarrow 涼亭海拔高度=435\sqrt 3+3, 故選\bbox[red, 2pt]{(D)}$$
========================= END ===========================
解題僅供參考,其他歷年試題及詳解


























沒有留言:
張貼留言