\(\bbox[blue,2pt]解:\)$$f(x)=m(x-2)^2+5 = mx^2-4mx+4m+5 \Rightarrow 4m+5=-3\\ \Rightarrow m=-2 \Rightarrow f(x)=-2x^2+8x-3 \\ \Rightarrow a=-2, b=8 \Rightarrow a+b=-2+8=6$$
\(\bbox[blue,2pt]解:\)
一根為-1+2i,則另一根為-1-2i因此\((x+1)^2=-4 \Rightarrow x^2+2x+5=0 \Rightarrow x^2+2x+5\)為其因式。利用長除法可得
因此 4=2(a-2)\(\Rightarrow\) a=4\(\Rightarrow\)(x+(a-2))=x+2為其因式,即另一實根為-2
故選\(\bbox[red,2pt]{(B)}\)
\(\bbox[blue,2pt]解:\)
f(0)=3\(\Rightarrow\)-3c=3\(\Rightarrow\)c=-1
f(-1)=4\(\Rightarrow\)4b=4\(\Rightarrow\)b=1
f(3)=24\(\Rightarrow\)12a=24\(\Rightarrow\)a=2
a+b+c=2+1+(-1)=2,故選\(\bbox[red,2pt]{(A)}\)
\(\bbox[blue,2pt]解:\)$$a={ \left( 0.125 \right) }^{ 0.25 }={ \left( \frac { 1 }{ 8 } \right) }^{ \frac { 1 }{ 4 } }\Rightarrow \log _{ 2 }{ a } =\log _{ 2 }{ { \left( \frac { 1 }{ 8 } \right) }^{ \frac { 1 }{ 4 } } } =\frac { 1 }{ 4 } \log _{ 2 }{ \left( \frac { 1 }{ 8 } \right) } \\ =\left( { 2 }^{ -2 } \right) \log _{ 2 }{ \left( { 2 }^{ -3 } \right) } =\left( { 2 }^{ -2 } \right) \times \left( -3 \right) =\frac { -3 }{ 4 } \Rightarrow a={ 2 }^{ -\frac { 3 }{ 4 } }\Rightarrow { 2 }^{ 0 }>a>{ 2 }^{ -1 }\\ \Rightarrow 1>a>\frac { 1 }{ 2 } $$
故選\(\bbox[red,2pt]{(C)}\)
\(\bbox[blue,2pt]解:\)$$2x+2\log { \left( 2+10^{ -x } \right) } -\log { \left( 1+4\cdot 10^{ x }+4\cdot 10^{ 2x } \right) } =2x+2\log { \left( 2+10^{ -x } \right) } -\log { { \left( 1+2\cdot { 10 }^{ x } \right) }^{ 2 } } \\ =2x+2\log { \left( 2+10^{ -x } \right) } -2\log { { \left( 1+2\cdot { 10 }^{ x } \right) } } =2x+2\log { \frac { 2+10^{ -x } }{ 1+2\cdot { 10 }^{ x } } } =\\ =2\left( x+\log { \frac { 2+10^{ -x } }{ 1+2\cdot { 10 }^{ x } } } \right) =2\left( \log { \frac { 2+10^{ -x } }{ 1+2\cdot { 10 }^{ x } } \times { 10 }^{ x } } \right) =2\log { \frac { 1+2\cdot { 10 }^{ x } }{ 1+2\cdot { 10 }^{ x } } } \\ =2\log { 1 } =2\times 0=0$$
故選\(\bbox[red,2pt]{(A)}\)
\(\bbox[blue,2pt]解:\)$$n={ 12 }^{ 100 }\Rightarrow \log { n } =\log { { 12 }^{ 100 } } =100\log { 12 } =100\left[ 2\log { 2 } +\log { 3 } \right] \\ =100\left[ 2\times 0.301+0.4771 \right] =100\times 1.0791=107.91=107+0.91\approx 107+\log { 8 } \\ \Rightarrow n={ 10 }^{ 107 }\times { 8}$$
故選\(\bbox[red,2pt]{(C)}\)
\(\bbox[blue,2pt]解:\)$$S=\sum _{ n=1 }^{ 10 }{ \frac { n }{ { 2 }^{ n-1 } } } =\frac { 1 }{ { 2 }^{ 0 } } +\frac { 2 }{ { 2 }^{ 1 } } +\frac { 3 }{ { 2 }^{ 2 } } +\cdots +\frac { 10 }{ { 2 }^{ 9 } } \\ \Rightarrow \frac { 1 }{ 2 } S=\frac { 1 }{ { 2 }^{ 1 } } +\frac { 2 }{ { 2 }^{ 2 } } +\frac { 3 }{ { 2 }^{ 3 } } +\cdots +\frac { 9 }{ { 2 }^{ 9 } } +\frac { 10 }{ { 2 }^{ 10 } } \\ \Rightarrow S-\frac { 1 }{ 2 } S=\frac { 1 }{ { 2 }^{ 0 } } +\frac { 1 }{ { 2 }^{ 1 } } +\frac { 1 }{ { 2 }^{ 2 } } +\cdots +\frac { 1 }{ { 2 }^{ 9 } } -\frac { 10 }{ { 2 }^{ 10 } } \\ \Rightarrow \frac { 1 }{ 2 } S=\frac { 1-{ \left( \frac { 1 }{ 2 } \right) }^{ 10 } }{ 1-\frac { 1 }{ 2 } } -\frac { 10 }{ { 2 }^{ 10 } } =2-\frac { 1 }{ { 2 }^{ 9 } } -\frac { 10 }{ { 2 }^{ 10 } } =2-\frac { 12 }{ { 2 }^{ 10 } } \\ \Rightarrow S=4-\frac { 12 }{ { 2 }^{ 9 } } \approx 4$$
故選\(\bbox[red,2pt]{(B)}\)
\(\bbox[blue,2pt]解:\)令此三位數為abc,其中abc互異、a不為0,c={0, 2, 4, 6}
c=0時,a有6種選法、b有5種選法,共有6x5=30種
c=2時,a有5種選法、b有5種選法,共有5x5=25種
c=4, c=6 皆與c=2相同,各有25種
所以共有30+25x3=105種三位數,故選\(\bbox[red,2pt]{(D)}\)
\(\bbox[blue,2pt]解:\)
\(H^3_6=C^8_6=C^8_2\),故選\(\bbox[red,2pt]{(B)}\)
\(\bbox[blue,2pt]解:\)
甲機器的不良品比率為\(\frac{50}{100}\times\frac{4}{100}=\frac{1}{50}\)
乙機器的不良品比率為\(\frac{30}{100}\times\frac{3}{100}=\frac{9}{1000}\)
丙機器的不良品比率為\(\frac{20}{100}\times\frac{2}{100}=\frac{1}{250}\)
不良品來自甲機器的比率為\(\frac{\frac{1}{50}}{\frac{1}{50}+\frac{9}{1000}+\frac{1}{250}} =\frac{\frac{1}{50}}{\frac{33}{1000}}=\frac{20}{33}\)
故選\(\bbox[red,2pt]{(D)}\)
\(\bbox[blue,2pt]解:\)
斜率=\(r_{xy}\times\frac{\sigma_y}{\sigma_x}=0.9\times\frac{2}{3}=\frac{3}{5}=0.6\),故選\(\bbox[red,2pt]{(B)}\)
\(\bbox[blue,2pt]解:\)$$由\begin{cases} \sin { \theta } +\cos { \theta } =\frac { -3 }{ 4 } \\ \sin { \theta } \cos { \theta } =\frac { k }{ 4 } \end{cases}可知\\ { \left( \sin { \theta } +\cos { \theta } \right) }^{ 2 }=\sin ^{ 2 }{ \theta } +\cos ^{ 2 }{ \theta } +2\sin { \theta } \cos { \theta } \\ \Rightarrow { \left( \frac { -3 }{ 4 } \right) }^{ 2 }=1+2\times \frac { k }{ 4 } \Rightarrow \frac { 9 }{ 16 } =1+\frac { k }{ 2 } \Rightarrow k=\frac { -7 }{ 8 } $$
故選\(\bbox[red,2pt]{(A)}\)
\(\bbox[blue,2pt]解:\)
sin A: sin B: sin C = a: b: c =2:3:4,令a=2k, b=3k, c=4k,利用餘弦定理:
\( a^2=b^2+c^2-2bc\cos{A} \Rightarrow 4k^2=9k^2+16k^2-24\cos{A}\)
\( \Rightarrow \cos{A}=\frac{21}{24}=\frac{7}{8}\Rightarrow \sin{A}=\frac{\sqrt{64-49}}{8}=\frac{\sqrt{15}}{8}\)
故選\(\bbox[red,2pt]{(B)}\)
\(\bbox[blue,2pt]解:\)
若圓心(1,2)至直線的距離等於半徑,表示圓與該直線相切。
圓心與直線\(2x-y=3\sqrt{5}\)的距離:\(\left|\frac{2-2-3\sqrt{5}}{\sqrt{5}}\right|=3\)
故選\(\bbox[red,2pt]{(D)}\)
\(\bbox[blue,2pt]解:\)$$\begin{vmatrix} a & b \\ c & d \end{vmatrix}=5\Rightarrow ad-bc=5\\ \begin{vmatrix} 3a+2b & a+3b \\ 3c+2d & c+3d \end{vmatrix}=\left( 3a+2b \right) \left( c+3d \right) -\left( a+3b \right) \left( 3c+2d \right) \\ =3ac+9ad+2bc+6bd-3ac-2ad-9bc-6bd\\ =7ad-7bc=7\left( ad-bc \right) =7\times 5=35$$
故選\(\bbox[red,2pt]{(B)}\)
\(\bbox[blue,2pt]解:\)
(a+b+c)(a+b-c)=ab \(\Rightarrow (a+b)^2-c^2=ab \Rightarrow a^2+b^2-c^2= -ab\)
利用餘弦定理:\(c^2=a^2+b^2-2ab\cos{C}\Rightarrow \cos{C}=\frac{a^2+b^2-c^2}{2ab}\)將上式代入,可得\(\cos{C}=\frac{-ab}{2ab}=\frac{-1}{2}\Rightarrow C=120^\circ\)
故選\(\bbox[red,2pt]{(D)}\)
\(\bbox[blue,2pt]解:\)
由於\(\overline{AD}\)為角平分線,所以\(\overline{AB}:\overline{AC} = \overline{BD}: \overline{DC}=2:3\)。因此令\(\overline{BD}=2k及\overline{DC}=3k, 並假設 \overline{AD}=x\)。
由餘弦定理可知:$$\begin{cases} 4k^{ 2 }=4+x^{ 2 }-4x\cos { 60^{ \circ } } \\ 9k^{ 2 }=9+x^{ 2 }-6x\cos { 60^{ \circ } } \end{cases}\Rightarrow \begin{cases} 4k^{ 2 }=4+x^{ 2 }-2x \\ 9k^{ 2 }=9+x^{ 2 }-3x \end{cases}\Rightarrow \begin{cases} 36k^{ 2 }=36+9x^{ 2 }-18x \\ 36k^{ 2 }=36+4x^{ 2 }-12x \end{cases}\\ \Rightarrow 5x^{ 2 }-6x=0\Rightarrow x(5x-6)=0\Rightarrow x=\frac { 6 }{ 5 } $$故選\(\bbox[red,2pt]{(B)}\)
\(\bbox[blue,2pt]解:\)$$令x=5\cos { \theta } +1,y=5\sin { \theta } +2\\ \Rightarrow 3x+4y=15\cos { \theta } +3+20\sin { \theta } +8=11+5\left( 3\cos { \theta } +4\sin { \theta } \right) \\ =11+25\left( \frac { 3 }{ 5 } \cos { \theta } +\frac { 4 }{ 5 } \sin { \theta } \right) =11+25\left( \sin { \alpha } \cos { \theta } +\cos { \alpha } \sin { \theta } \right) \\ =11+25\sin { \left( \alpha +\theta \right) } \Rightarrow 最大值為11+25=36$$
故選\(\bbox[red,2pt]{(C)}\)
\(\bbox[blue,2pt]解:\)
2x+3y=4在xy平面上為一直線,在三度空間中為一平面並與XY平面垂直,故選\(\bbox[red,2pt]{(B)}\)
\(\bbox[blue,2pt]解:\)$$令\triangle =\begin{vmatrix} a_{ 1 } & b_{ 1 } & c_{ 1 } \\ a_{ 2 } & b_{ 2 } & c_{ 2 } \\ a_{ 3 } & b_{ 3 } & c_{ 3 } \end{vmatrix},\triangle x=\begin{vmatrix} d_{ 1 } & b_{ 1 } & c_{ 1 } \\ d_{ 2 } & b_{ 2 } & c_{ 2 } \\ d_{ 3 } & b_{ 3 } & c_{ 3 } \end{vmatrix},\triangle y=\begin{vmatrix} a_{ 1 } & d_{ 1 } & c_{ 1 } \\ a_{ 2 } & d_{ 2 } & c_{ 2 } \\ a_{ 3 } & d_{ 3 } & c_{ 3 } \end{vmatrix},\triangle z=\begin{vmatrix} a_{ 1 } & b_{ 1 } & d_{ 1 } \\ a_{ 2 } & b_{ 2 } & d_{ 2 } \\ a_{ 3 } & b_{ 3 } & d_{ 3 } \end{vmatrix}\\ 依題意:第1組聯立方程組的解為x=\frac { \triangle x }{ \triangle } =1,y=\frac { \triangle y }{ \triangle } =2,z=\frac { \triangle z }{ \triangle } =3\\ 第2組聯立方程組的解為x=\frac { \begin{vmatrix} 3d_{ 1 } & 2b_{ 1 } & 9c_{ 1 } \\ 3d_{ 2 } & 2b_{ 2 } & 9c_{ 2 } \\ 3d_{ 3 } & 2b_{ 3 } & 9c_{ 3 } \end{vmatrix} }{ \begin{vmatrix} 3a_{ 1 } & 2b_{ 1 } & 9c_{ 1 } \\ 3a_{ 2 } & 2b_{ 2 } & 9c_{ 2 } \\ 3a_{ 3 } & 2b_{ 3 } & 9c_{ 3 } \end{vmatrix} } =\frac { 3\times 2\times 9\times \triangle x }{ 3\times 2\times 9\times \triangle } =\frac { \triangle x }{ \triangle } =1\\ y=\frac { \begin{vmatrix} 3a_{ 1 } & 3d_{ 1 } & 9c_{ 1 } \\ 3a_{ 2 } & 3d_{ 2 } & 9c_{ 2 } \\ 3a_{ 3 } & 3d_{ 3 } & 9c_{ 3 } \end{vmatrix} }{ \begin{vmatrix} 3a_{ 1 } & 2b_{ 1 } & 9c_{ 1 } \\ 3a_{ 2 } & 2b_{ 2 } & 9c_{ 2 } \\ 3a_{ 3 } & 2b_{ 3 } & 9c_{ 3 } \end{vmatrix} } =\frac { 3\times 3\times 9\times \triangle y }{ 3\times 2\times 9\times \triangle } =\frac { 3\triangle y }{ 2\triangle } =\frac { 3 }{ 2 } \times 2=3\\ z=\frac { \begin{vmatrix} 3a_{ 1 } & 2b_{ 1 } & 3d_{ 1 } \\ 3a_{ 2 } & 2b_{ 2 } & 3d_{ 2 } \\ 3a_{ 3 } & 2b_{ 3 } & 3d_{ 3 } \end{vmatrix} }{ \begin{vmatrix} 3a_{ 1 } & 2b_{ 1 } & 9c_{ 1 } \\ 3a_{ 2 } & 2b_{ 2 } & 9c_{ 2 } \\ 3a_{ 3 } & 2b_{ 3 } & 9c_{ 3 } \end{vmatrix} } =\frac { 3\times 2\times 3\times \triangle y }{ 3\times 2\times 9\times \triangle } =\frac { \triangle z }{ 3\triangle } =\frac { 1 }{ 3 } \times 3=1\\ \Rightarrow 第2組聯立方程組的解為(1,3,1)$$
故選\(\bbox[red,2pt]{(D)}\)
\(\bbox[blue,2pt]解:\)
$$\triangle ABC面積=\frac { 1 }{ 2 } \begin{vmatrix} 1 & 2 \\ 3 & 6 \\ -2 & 4 \\ 1 & 2 \end{vmatrix}=\frac { 1 }{ 2 } \left[ 6+12-4-6+12-4 \right] =8\\ \left| M \right| =\begin{vmatrix} 1 & 4 \\ 2 & 5 \end{vmatrix}=\left| 5-8 \right| =3\Rightarrow 轉換後的面積=8\times 3=24$$
故選\(\bbox[red,2pt]{(C)}\)
\(\bbox[blue,2pt]解:\)
在X軸的投影長為a, 在Y軸的投影長為b, 在Z軸的投影長為c, 則$$\begin{cases} a^{ 2 }+b^{ 2 }=(\sqrt { 23 } )^{ 2 }=23 \\ b^{ 2 }+c^{ 2 }=(\sqrt { 24 } )^{ 2 }=24 \\ c^{ 2 }+a^{ 2 }=5^{ 2 }=25 \end{cases}\Rightarrow 2(a^{ 2 }+b^{ 2 }+c^{ 2 })=72\\ \Rightarrow a^{ 2 }+b^{ 2 }+c^{ 2 }=36\Rightarrow \sqrt { a^{ 2 }+b^{ 2 }+c^{ 2 } } =\overline { AB } =\sqrt { 36 } =6$$
故選\(\bbox[red,2pt]{(B)}\)
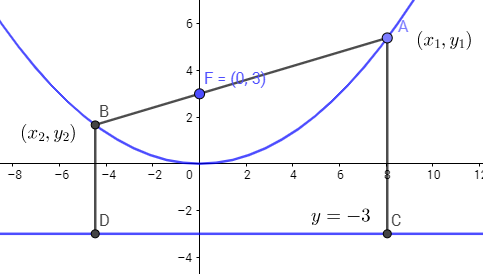
\(\bbox[blue,2pt]解:\)
由拋物線方程式可知:c=3, 焦點F=(0,3),準線方程式為y=-3
由拋物線定義可知: \(\overline{AC}=\overline{AF}\Rightarrow \overline{AF}=y_1+3\),同理 \(\overline{BF}=y_2+3\)。因此\(y_1+3+y_2+3 = \overline{AF}+\overline{FB}\Rightarrow y_1+y_2 = \overline{AB}-6 = 16-6=10\),故選\(\bbox[red,2pt]{(A)}\)。
\(\bbox[blue,2pt]解:\)
由兩焦點距離=5-(-5)=10可知c=10/2=5,又漸近線斜率為-3/4,所以a=4,b=3,貫軸長=2a=8,故選\(\bbox[red,2pt]{(B)}\)
\(\bbox[blue,2pt]解:\)
取出黑球的機率為4/9,期望值為\(\frac{4}{9}\times 5=\frac{20}{9}\)
取出白球的機率為5/9,期望值為\(\frac{5}{9}\times 14=\frac{70}{9}\)
因此取球獎金為\(\frac{20}{9}+\frac{70}{9}=\frac{90}{9}=10\)
故選\(\bbox[red,2pt]{(B)}\)
\(\bbox[blue,2pt]解:\)
資訊不足(未註明選舉人數),無法推算
故選\(\bbox[red,2pt]{(??)}\)
\(\bbox[blue,2pt]解:\)題目有誤,應該是$$\frac { { \left( \cos { 6° } +i\sin { 6° } \right) }^{ 20 }{ \left( \cos { 4° } +i\sin { 4° } \right) }^{ 30 } }{ { \left( \cos { 5° } -i\sin { 5° } \right) }^{ 12 } } =\frac { \left( \cos { 120° } +i\sin { 120° } \right) \left( \cos { 120° } +i\sin { 120° } \right) }{ \cos { 60° } -i\sin { 60° } } \\ =\frac { \cos { 240° } +i\sin { 240° } }{ \cos { 60° } -i\sin { 60° } } =\frac { -\frac { 1 }{ 2 } -\frac { \sqrt { 3 } i }{ 2 } }{ \frac { 1 }{ 2 } -\frac { \sqrt { 3 } i }{ 2 } } =\frac { -1-\sqrt { 3 } i }{ 1-\sqrt { 3 } i } =\frac { \left( -1-\sqrt { 3 } i \right) \left( 1+\sqrt { 3 } i \right) }{ \left( 1-\sqrt { 3 } i \right) \left( 1+\sqrt { 3 } i \right) } \\ =\frac { 2-2\sqrt { 3 } i }{ 4 } =\frac { 1-\sqrt { 3 } i }{ 2 } $$故選\(\bbox[red,2pt]{(B)}\)
\(\bbox[blue,2pt]解:\)$$\\ f\left( x \right) =3\sin { x } +4\cos { x } +5=5+5\left( \frac { 3 }{ 5 } \sin { x } +\frac { 4 }{ 5 } \cos { x } \right)\\ =5+5\left( \cos { y } \sin { x } +\sin { y } \cos { x } \right) =5+5\sin { \left( x+y \right) } \Rightarrow 最大值為5+5=10$$
故選\(\bbox[red,2pt]{(C)}\)
\(\bbox[blue,2pt]解:\)
\(\cos{\frac{7\pi}{4}}=1,\cos{\frac{7\pi}{4}}=-1\),故選\(\bbox[red,2pt]{(D)}\)
\(\bbox[blue,2pt]解:\)
\(3\pi<{\pi}^2<3\pi+\frac{1}{2}\pi\Rightarrow \frac{-1}{2}\le\sin{\pi^2}<0\),故選\(\bbox[red,2pt]{(C)}\)
\(\bbox[blue,2pt]解:\)
i-1為一虛根,則另一虛根為-i-1,所以\(x^2+2x+2\)為其因式,另一為實根。
若\(\frac{b}{a}為其有理根\Rightarrow (ax-b)為f(x)的因式\Rightarrow f(x)=k(ax-b)(x^2+2x+2) \)
a,b 為整數,但k為實數,所以(D)不一定成立。
故選\(\bbox[red,2pt]{(BE)}\)
\(\bbox[blue,2pt]解:\)
(E) \(4>2>1\Rightarrow \log _{ 4 }{ 2 } =\frac { 1 }{ 2 } <1\)
只有(E)錯誤,故選\(\bbox[red,2pt]{(ABCD)}\)
\(\bbox[blue,2pt]解:\)
(A) 滿足\(P(A\cap B)=P(A)P(B)\),則A, B獨立;A,B交集為空集合,不一定獨立。
(D)互斥代表A,B交集為空集合,與選項(A)相同
(E)三事件獨立需為兩兩獨立且\(P(A\cap B\cap C)=P(A)P(B)P(C)\),選項(E)少一條件
故選\(\bbox[red,2pt]{(BC)}\)
\(\bbox[blue,2pt]解:\)
酒杯相異,杯中飲料相異,則第一杯有5種選擇,第二杯有4種選擇,第三杯月3種選擇,共有5 x 4 x 3= 60 = \(P^5_3\),選項(E)錯誤。
故選\(\bbox[red,2pt]{(ABCD)}\)
\(\bbox[blue,2pt]解:\)
令迴歸直線方程式為 y=mx+n,該直線通(0,1),所以直線方程式為 y=mx+1
\(1=\mu_y-m\mu_x\Rightarrow 1=3-2m \Rightarrow m=1\Rightarrow\) 直線方程式為y=x+1
又\(m=r_{xy}\times\frac{\sigma_y}{\sigma_x}\Rightarrow 1=\frac{4}{5}\times\frac{\sigma_y}{\sigma_x}\Rightarrow \sigma_x<\sigma_y\)
故選\(\bbox[red,2pt]{(ACD)}\)
\(\bbox[blue,2pt]解:\)$$(A)\pi <\theta <\frac { 3\pi }{ 2 } \Rightarrow \frac { \pi }{ 2 } <\frac { \theta }{ 2 } <\frac { 3\pi }{ 4 } \Rightarrow \sin { \frac { \theta }{ 2 } } >0\\ (B)\sin { \theta } =-\frac { 3 }{ 5 } ,\pi <\theta <\frac { 3\pi }{ 2 } \Rightarrow \cos { \theta } =\frac { -4 }{ 5 } \\ (C)\tan { \theta } =\frac { \sin { \theta } }{ \cos { \theta } } =\frac { 3 }{ 4 } \\ (D)\sin { 2\theta } =2\sin { \theta } \cos { \theta } =2\times \frac { -3 }{ 5 } \times \frac { -4 }{ 5 } =\frac { 24 }{ 25 } \\ (E)\cos { 2\theta } =\cos ^{ 2 }{ \theta } -\sin ^{ 2 }{ \theta } =\frac { 16 }{ 25 } -\frac { 9 }{ 25 } =\frac { 7 }{ 25 } $$
故選\(\bbox[red,2pt]{(BDE)}\)
\(\bbox[blue,2pt]解:\)
(E)若a為零向量,則不一定成立,故選\(\bbox[red,2pt]{(ABCD)}\)
\(\bbox[blue,2pt]解:\)
(A)三點若在同一直線上,仍無法決定一平面
(E)歪斜表示不在同一平面上
故選\(\bbox[red,2pt]{(BCD)}\)
\(\bbox[blue,2pt]解:\)
(A) AB不一定等於BA
(C)\(\begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix}\begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix}=\begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix}\)
(E)若B=0, 則\(B^2\ne B^2+I\)
故選\(\bbox[red,2pt]{(BD)}\)
\(\bbox[blue,2pt]解:\)
(E)的圖形如上圖,週期為\(2\pi\),其它圖形的週期為\(\pi\),故選\(\bbox[red,2pt]{(ABCD)}\)
-- END --











































沒有留言:
張貼留言