\(\bbox[blue,2pt]解：\)$${ 16 }^{ 2 }=256<\sqrt { 257 } <17^{ 2 } =289\\ \Rightarrow \sqrt { 9+\sqrt { 257 } } =\sqrt { 9+16.XX } =\sqrt { 25.XXX } =5.YYY$$
故選\(\bbox[red,2pt]{(C)}\)
\(\bbox[blue,2pt]解：\)$$x\sqrt { 6-\sqrt { 20 } } +y\sqrt { 9+4\sqrt { 5 } } =x\sqrt { 6-2\sqrt { 5 } } +y\sqrt { 9+4\sqrt { 5 } } \\ =x\left( \sqrt { 5 } -1 \right) +y\left( \sqrt { 5 } +2 \right) =\left( -x+2y \right) +\left( x+y \right) \sqrt { 5 } =5+\sqrt { 5 } \\ \Rightarrow \begin{cases} -x+2y=5 \\ x+y=1 \end{cases}\Rightarrow (x,y)=(-1,2)$$
故選\(\bbox[red,2pt]{(B)}\)
\(\bbox[blue,2pt]解：\)$$\frac { 3x+4y }{ 2 } \le \sqrt { 3x\cdot 4y } \Rightarrow \frac { 24 }{ 2 } \le \sqrt { 12xy } \Rightarrow 12^{ 2 }\le 12xy\Rightarrow 12\le xy$$
故選\(\bbox[red,2pt]{(A)}\)
\(\bbox[blue,2pt]解：\)$$f\left( x \right) =x^{ 3 }+5x^{ 2 }+10x+10=(x+1)(x^{ 2 }+4x+6)+4\\ =\left( x+1 \right) \left[ \left( x+1 \right) \left( x+3 \right) +3 \right] +4=\left( x+1 \right) \left[ \left( x+1 \right) \left( (x+1)+2 \right) +3 \right] +4\\ =\left( x+1 \right) \left[ \left( x+1 \right) ^{ 2 }+2(x+1)+3 \right] +4=\left( x+1 \right) ^{ 3 }+2\left( x+1 \right) ^{ 2 }+3(x+1)+4\\ \Rightarrow \left( a,b,c,d \right) =\left( 1,2,3,4 \right) $$
故選\(\bbox[red,2pt]{(D)}\)
\(\bbox[blue,2pt]解：\)$$-3x^{ 2 }+3x-5=-3{ \left( x-\frac { 1 }{ 2 } \right) }^{ 2 }-\frac { 17 }{ 4 } <0\\ \left( -3x^{ 2 }+3x-5 \right) \left( x^{ 2 }-ax+b \right) \ge 0\Rightarrow x^{ 2 }-ax+b\le 0\\ \Rightarrow x^{ 2 }-ax+b=\left( x+1 \right) \left( x-3 \right) \Rightarrow a=2,b=-3$$
故選\(\bbox[red,2pt]{(B)}\)
\(\bbox[blue,2pt]解：\)$${ 4 }^{ x }=7\Rightarrow { 2 }^{ 2x }=7\Rightarrow { \left( { 2 }^{ x } \right) }^{ 2 }=7\Rightarrow { 2 }^{ x }=\sqrt { 7 } \\ { \Rightarrow 2 }^{ x+3 }-{ 8 }^{ x }=8\cdot { 2 }^{ x }-{ \left( { 2 }^{ x } \right) }^{ 3 }=8\sqrt { 7 } -7\sqrt { 7 } =\sqrt { 7 } $$
故選\(\bbox[red,2pt]{(A)}\)
\(\bbox[blue,2pt]解：\)$$f\left( b \right) -f\left( a \right) =-2\Rightarrow \log _{ \sqrt { 5 } }{ b } -\log _{ \sqrt { 5 } }{ a } =-2\Rightarrow \log _{ \sqrt { 5 } }{ \frac { b }{ a } } =-2\\ \Rightarrow \frac { b }{ a } ={ \sqrt { 5 } }^{ -2 }=\frac { 1 }{ 5 } \Rightarrow \frac { a }{ b } =5$$
故選\(\bbox[red,2pt]{(D)}\)
\(\bbox[blue,2pt]解：\)$${ a }_{ n+1 }=\frac { n+1 }{ n+2 } { a }_{ n }\Rightarrow { a }_{ 100 }=\frac { 100 }{ 101 } { a }_{ 99 }=\frac { 100 }{ 101 } \cdot \frac { 99 }{ 100 } { a }_{ 98 }\\ =\frac { 100 }{ 101 } \cdot \frac { 99 }{ 100 } \cdot \frac { 98 }{ 99 } \cdot \cdots \cdot \frac { 2 }{ 3 } { a }_{ 1 }=\frac { 100 }{ 101 } \cdot \frac { 99 }{ 100 } \cdot \frac { 98 }{ 99 } \cdot \cdots \cdot \frac { 2 }{ 3 } \cdot \frac { 1 }{ 2 } \\ =\frac { 1 }{ 101 } $$
故選\(\bbox[red,2pt]{(C)}\)
\(\bbox[blue,2pt]解：\)$$S=\sum _{ n=1 }^{ 20 }{ \left[ \left( 2n-1 \right) \left( 2n \right) \right] } =\sum _{ n=1 }^{ 20 }{ \left[ 4n^{ 2 }-2n \right] } =4\sum _{ n=1 }^{ 20 }{ n^{ 2 } } -2\sum _{ n=1 }^{ 20 }{ n } \\ =4\cdot \frac { 20\cdot 21\cdot 41 }{ 6 } -2\cdot \frac { 20\cdot 21 }{ 2 } =11480-420=11060$$
故選\(\bbox[red,2pt]{(A)}\)
\(\bbox[blue,2pt]解：\)
將3與4綁在一起，有兩種{34}或{43}簡寫成A、
將5與6綁在一起，有兩種{56}或{65}簡寫成B、
將7與8綁在一起，有兩種{78}或{87}簡寫成C、
則題意變成1、2、A、B、C五個數字排列，但1與2不相鄰。，
相當於所有可能減去1與2相鄰的排列:
所有可能5!，將1與2綁在一起變成四個數字共有4!x2，所以有5!-4!x2=120-48=72種數字。
由於A、B、C各有2種情形，所以總共有72x2x2x2=576種，故選\(\bbox[red,2pt]{(B)}\)
\(\bbox[blue,2pt]解：\)$$C^{ n }_{ 2 }=78\Rightarrow \frac { n\times \left( n-1 \right) }{ 2 } =78\Rightarrow n^{ 2 }-n-156=0\\ \Rightarrow \left( n-13 \right) \left( n+12 \right) =0\Rightarrow n=13$$
故選\(\bbox[red,2pt]{(D)}\)
\(\bbox[blue,2pt]解：\)$${ \left( x+y \right) }^{ 11 }=\sum _{ n=0 }^{ 11 }{ C^{ 11 }_{ n }x^{ n }y^{ 11-n } } \Rightarrow { \left( 1+1 \right) }^{ 11 }=\sum _{ n=0 }^{ 11 }{ C^{ 11 }_{ n } } \\ \Rightarrow { 2 }^{ 11 }=C^{ 11 }_{ 0 }+C^{ 11 }_{ 1 }+\cdots +C^{ 11 }_{ 10 }+C^{ 11 }_{ 11 }\\ \Rightarrow C^{ 11 }_{ 1 }+\cdots +C^{ 11 }_{ 10 }={ 2 }^{ 11 }-C^{ 11 }_{ 0 }-C^{ 11 }_{ 11 }=2048-1-1=2046$$
故選\(\bbox[red,2pt]{(C)}\)
\(\bbox[blue,2pt]解：\)
30個正整數取出3個數，共有\(C^{30}_3\)種取法；
30個正整數中有15個偶數及15個奇數，15個偶數取出2個偶數共有\(C^{15}_2\)種可能，15個奇數取出1個奇數共有15種選法；
機率為\(\frac{C^{15}_2\cdot 15}{C^{30}_3}=\frac{45}{116}\)
故選\(\bbox[red,2pt]{(C)}\)
\(\bbox[blue,2pt]解：\)
7排在第六位○○○○○7○共有6!種排法，
7排在第六位且6排在第七位○○○○○76機率為5!，機率為5!/6!=1/6，故選\(\bbox[red,2pt]{(A)}\)
\(\bbox[blue,2pt]解：\)
三角形大角對大邊，由\(a^2=b^2+c^2+bc\)可知\(\angle A\)為最大角。
由餘弦定理: \( a^2=b^2+c^2-2bc\cos{A}=b^2+c^2+bc\Rightarrow \cos{A}=\frac{-1}{2}\)
故選\(\bbox[red,2pt]{(B)}\)
\(\bbox[blue,2pt]解：\)
由於A、B、C三點對氣球的仰角都是60度，所以A、B、C在同一圓上，如上圖。
氣球高度\(\overline{OP}=半徑\times\sqrt{3}=40\sqrt{3}\)，故選\(\bbox[red,2pt]{(D)}\)
\(\bbox[blue,2pt]解：\)
令\(\angle APB=2\theta \Rightarrow \angle OPB=\theta \Rightarrow \sin{\theta}=\frac{3}{\sqrt{10}}, \cos{\theta}=\frac{1}{\sqrt{10}}\)
\(\Rightarrow \sin{2\theta}=2\sin{\theta}\cos{\theta}=2\times\frac{3}{\sqrt{10}}\times\frac{1}{\sqrt{10}}=\frac{6}{10}=\frac{3}{5}\)，故選\(\bbox[red,2pt]{(C)}\)
\(\bbox[blue,2pt]解：\)$$\left(\vec{a}+t\vec{b}\right)=\left(-3-t,1+2t\right)\Rightarrow \left(\vec{a}+t\vec{b}\right)\cdot \vec{a}= \left(-3-t,1+2t\right)\cdot (-3,1)\\ =9+3t+1+2t =5t+10 =0 \Rightarrow t=-2 $$
故選\(\bbox[red,2pt]{(B)}\)
\(\bbox[blue,2pt]解：\)$$\begin{vmatrix} 9 & 5 \\ 2 & 7 \end{vmatrix}=63-10=53$$
故選\(\bbox[red,2pt]{(A)}\)
\(\bbox[blue,2pt]解：\)$$\overrightarrow { AB } =\left( 6-2,4-5,5-4 \right) =\left( 4,-1,1 \right) ,\overrightarrow { AC } =\left( 3-2,6-5,4-4 \right) =\left( 1,1,0 \right) \\ \Rightarrow \cos { \angle BAC } =\frac { \overrightarrow { AB } \cdot \overrightarrow { AC } }{ \left| \overrightarrow { AB } \right| \left| \overrightarrow { AC } \right| } =\frac { 4-1+0 }{ \sqrt { 16+1+1 } \sqrt { 1+1 } } =\frac { 3 }{ \sqrt { 36 } } =\frac { 1 }{ 2 } \\ \Rightarrow \angle BAC=60°$$
故選\(\bbox[red,2pt]{(C)}\)
\(\bbox[blue,2pt]解：\)$$\left| \left( \vec { a } \times \vec { b } \right) \cdot \vec { c } \right| =\left| \left( \begin{vmatrix} 4 & 2 \\ -2 & 2 \end{vmatrix},\begin{vmatrix} 2 & 4 \\ 2 & 4 \end{vmatrix},\begin{vmatrix} 4 & 4 \\ 4 & -2 \end{vmatrix} \right) \cdot \left( 2,6,2 \right) \right| =\left| \left( 12,0,-24 \right) \cdot \left( 2,6,2 \right) \right| \\ =\left| 24-48 \right| =24$$
故選\(\bbox[red,2pt]{(D)}\)
\(\bbox[blue,2pt]解：\)
令平面方程式為ax+by+cz+d=0，將A、B、C三點代入可得2x+2y+z-2=0。
(0,0,0)至平面距離為\(\left|\frac{-2}{\sqrt{4+4+1}}\right|=\frac{2}{3}\)，故選\(\bbox[red,2pt]{(B)}\)
\(\bbox[blue,2pt]解：\)$$\begin{vmatrix} -2 & 1 & -1 \\ 1 & 2 & 3 \\ -1 & a & 2 \end{vmatrix}=0\Rightarrow -15+5a=0\Rightarrow a=3\Rightarrow \begin{cases} -2x+y-z=3 \\ x+2y+3z=1 \\ -x+3y+2z=b \end{cases}\\ \begin{cases} -2x+y-z=3 \\ x+2y+3z=1 \end{cases}\Rightarrow \begin{cases} x=y-2 \\ z=1-y \end{cases}\Rightarrow -(y-2)+3y+2(1-y)=b\Rightarrow b=4$$
故選\(\bbox[red,2pt]{(A)}\)
\(\bbox[blue,2pt]解：\)$$\begin{bmatrix} 0.8 & 0.4 \\ 0.2 & 0.6 \end{bmatrix}\begin{bmatrix} p \\ 1-p \end{bmatrix}=\begin{bmatrix} p \\ 1-p \end{bmatrix}\Rightarrow 0.8p+0.4(1-p)=p\Rightarrow p=\frac { 2 }{ 3 } $$
故選\(\bbox[red,2pt]{(D)}\)
\(\bbox[blue,2pt]解：\)
\(x^{ 2 }+2x+4y=11\Rightarrow { \left( x+1 \right) }^{ 2 }=-4(y-3) \Rightarrow\) 頂點坐標為(-1,3)，焦點坐標為(-1, 3-1)=(-1, 2)，故選\(\bbox[red,2pt]{(B)}\)
\(\bbox[blue,2pt]解：\)
由題意可知：兩焦點坐標分別為(0,3)及(0,-3)，因此中心坐標為(0, 0)，長軸為10，直立式的橢圓，故選\(\bbox[red,2pt]{(C)}\)
\(\bbox[blue,2pt]解：\)
只有甲命中的機率 = \(\frac{1}{2}\times\frac{2}{3}\times\frac{3}{4}=\frac{1}{4}\)
只有乙命中的機率 = \(\frac{1}{2}\times\frac{1}{3}\times\frac{3}{4}=\frac{1}{8}\)
只有丙命中的機率 = \(\frac{1}{2}\times\frac{2}{3}\times\frac{1}{4}=\frac{1}{12}\)
三者相加 = \(\frac{6+3+2}{24}=\frac{11}{24}\)，故選\(\bbox[red,2pt]{(B)}\)
\(\bbox[blue,2pt]解：\)
二項分布的變異數=np(1-p)=400x0.5x0.5=100，故選\(\bbox[red,2pt]{(A)}\)
\(\bbox[blue,2pt]解：\)$$令圓半徑=r\Rightarrow 3\pi =r\times \frac { \pi }{ 4 } \Rightarrow r=12\Rightarrow 圓面積={ r }^{ 2 }\pi =144\pi \\ \Rightarrow 扇形面積=144\pi \times \frac { \frac { \pi }{ 4 } }{ 2\pi } =144\pi \times \frac { 1 }{ 8 } =18\pi $$
故選\(\bbox[red,2pt]{(A)}\)
\(\bbox[blue,2pt]解：\)
(A)最大值為1, (B)最小值為-1 (C)sin(0)=0，有通過原點；故選\(\bbox[red,2pt]{(D)}\)
\(\bbox[blue,2pt]解：\)$$(A)a+b=\frac { \sqrt { 5 } }{ \sqrt { 5 } +2 } +\frac { \sqrt { 5 } }{ \sqrt { 5 } -2 } =\frac { \sqrt { 5 } \times 2\sqrt { 5 } }{ \left( \sqrt { 5 } +2 \right) \left( \sqrt { 5 } -2 \right) } =10\\ (B)ab=\frac { \sqrt { 5 } }{ \sqrt { 5 } +2 } \cdot \frac { \sqrt { 5 } }{ \sqrt { 5 } -2 } =\frac { 5 }{ 1 } =5\\ (C)\frac { 1 }{ a } +\frac { 1 }{ b } =\frac { a+b }{ ab } =\frac { 10 }{ 5 } =2\\ (D)a^{ 2 }+b^{ 2 }={ \left( a+b \right) }^{ 2 }-2ab={ 10 }^{ 2 }-2\cdot 5=100-10=90\\ (E)a^{ 3 }+b^{ 3 }=\left( a+b \right) \left( a^{ 2 }-ab+b^{ 2 } \right) =10\left( 90-5 \right) =850$$
故選\(\bbox[red,2pt]{(ADE)}\)
\(\bbox[blue,2pt]解：\)$$2x^3+x^2-8x-4=0\Rightarrow x^2(2x+1)-4(2x+1)=0 \Rightarrow (x^2-4)(2x+1)=0 \\ \Rightarrow (x+2)(x-2)(2x+1)=0 \Rightarrow x=2, -2, \frac{-1}{2}$$
故選\(\bbox[red,2pt]{(BDE)}\)
\(\bbox[blue,2pt]解：\)
故選\(\bbox[red,2pt]{(ABC)}\)
\(\bbox[blue,2pt]解：\)$${ \left( x+\frac { 3 }{ x } \right) }^{ 6 }=\sum _{ n=0 }^{ 6 }{ C^{ 6 }_{ n }{ x }^{ n }{ \left( \frac { 3 }{ x } \right) }^{ 6-n } } =\sum _{ n=0 }^{ 6 }{ { 3 }^{ 6-n }C^{ 6 }_{ n }{ x }^{ 2n-6 } } \\ \Rightarrow { x }^{ 6 }係數=C^{ 6 }_{ 6 }=1\\ \Rightarrow { x }^{ 5 }係數=0\\ \Rightarrow { x }^{ 4 }係數={ 3 }^{ 6-5 }\times C^{ 6 }_{ 5 }=3\times 6=18\\ \Rightarrow { x }^{ 2 }係數={ 3 }^{ 6-4 }\times C^{ 6 }_{ 4 }=9\times 15=135\\ \Rightarrow 常數項={ 3 }^{ 6-3 }\times C^{ 6 }_{ 3 }=27\times 20=540$$
故選\(\bbox[red,2pt]{(BD)}\)
\(\bbox[blue,2pt]解：\)
\(\sigma_y = |a|\sigma_x\Rightarrow 6=a\cdot 12\Rightarrow a=\frac{1}{2}\)，又\(\mu_y=a\cdot \mu_x+b\Rightarrow 50=\frac{1}{2}\cdot 30+b\Rightarrow b=35\)
故選\(\bbox[red,2pt]{(AE)}\)
\(\bbox[blue,2pt]解：\)
\(\bbox[blue,2pt]解：\)
由聯立不等式可求出四直線之交點，分別為A、B、C、D，再代入x-2y可得
代入A→x-2y=3-8=-5；代入B→x-2y=4-4=0；代入C→x-2y=1；代入D→x-2y=0-4=-4
因此最大值為1, 最小值-5，故選\(\bbox[red,2pt]{(BC)}\)
\(\bbox[blue,2pt]解：\)$$令x=10\sin { \theta } ,y=10\cos { \theta } \Rightarrow 3x-4y=30\sin { \theta } -40\cos { \theta } =50\left( \frac { 3 }{ 5 } \sin { \theta } -\frac { 4 }{ 5 } \cos { \theta } \right) \\ =50\left( \cos { \alpha } \sin { \theta } -\sin { \alpha } \cos { \theta } \right) =50\sin { (\theta-\alpha) } $$因此最大值為50, 最小值為-50。$$3x-4y=50\Rightarrow y=\frac { 3 }{ 4 } x-\frac { 25 }{ 2 } \Rightarrow { x }^{ 2 }+{ \left( \frac { 3 }{ 4 } x-\frac { 25 }{ 2 } \right) }^{ 2 }=100\\ \Rightarrow \frac { 25 }{ 16 } { x }^{ 2 }-\frac { 75 }{ 4 } x+\frac { 225 }{ 4 } =0\Rightarrow { \left( x-6 \right) }^{ 2 }=0\\ \Rightarrow x=6\Rightarrow y=\frac { 3 }{ 4 } \times 6-\frac { 25 }{ 2 } =\frac { 9 }{ 2 } -\frac { 25 }{ 2 } =-8$$
故選\(\bbox[red,2pt]{(CDE)}\)
\(\bbox[blue,2pt]解：\)$$過A,B兩點之直線方程式L:\frac { x }{ -2 } =\frac { y-1 }{ 2 } =\frac { z-2 }{ -2 } $$各點均符合L，故選\(\bbox[red,2pt]{(ABCDE)}\)
\(\bbox[blue,2pt]解：\)$$\begin{cases} AB=\begin{bmatrix} 5 & 6 \\ 7 & 8 \end{bmatrix}\begin{bmatrix} 9 & -4 \\ -8 & 7 \end{bmatrix}=\begin{bmatrix} 45-48 & -20+42 \\ 63-64 & -28+56 \end{bmatrix}=\begin{bmatrix} -3 & 22 \\ -1 & 28 \end{bmatrix} \\ BA=\begin{bmatrix} 9 & -4 \\ -8 & 7 \end{bmatrix}\begin{bmatrix} 5 & 6 \\ 7 & 8 \end{bmatrix}=\begin{bmatrix} 45-28 & 54-32 \\ -40+49 & -48+56 \end{bmatrix}=\begin{bmatrix} 17 & 22 \\ 9 & 8 \end{bmatrix} \end{cases}\\ \Rightarrow AB\neq BA\Rightarrow (A+B)(A-B)\neq A^2-B^2$$
故選\(\bbox[red,2pt]{(BCE)}\)
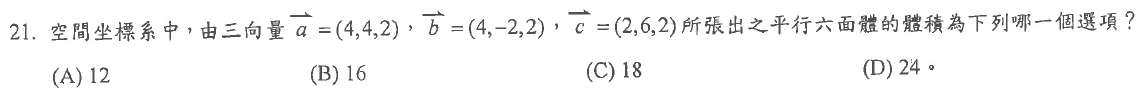
沒有留言:
張貼留言