朱式幸福: 105年警專35期甲組數學科詳解

解：

$\begin{cases} \left| y+3 \right| =2 \\ \left| x+1 \right| =0 \end{cases}\Rightarrow \begin{cases} y=-1,-5 \\ x=-1 \end{cases}\Rightarrow (x,y)=(-1,-1),(-1,-5)\\ \begin{cases} \left| y+3 \right| =1 \\ \left| x+1 \right| =2 \end{cases}\Rightarrow \begin{cases} y=-2,-4 \\ x=1,-3 \end{cases}\Rightarrow (x,y)=(1,-2),(1,-4),(-3,-2),(-3,-4)\\ \begin{cases} \left| y+3 \right| =0 \\ \left| x+1 \right| =4 \end{cases}\Rightarrow \begin{cases} y=-3 \\ x=3,-5 \end{cases}\Rightarrow (x,y)=(3,-3),(-5,-3)$ 共有8組解，故選(A)。

解：依題意

$f(x)=-3(x-2)^2+7 = -3x^2+12x-5 \Rightarrow$ a=12,b=-5，因此a+b=7，故選(D)。

解：

令f(x)=P(x)(x-1)(x+1)+Q(x)，其中Q(x)為餘式，

取

$x^2=1\Rightarrow f(x)=x^{105}+2x-3=x^{104}\times x+2x-3 = x+2x-3=3x-3$ ，
因此Q(x)=3x-3，故選(C)。

解：

$-\frac { 1 }{ 3 } \le x\le \frac { 5 }{ 2 } \Rightarrow \left( x+\frac { 1 }{ 3 } \right) \left( x-\frac { 5 }{ 2 } \right) \le 0\Rightarrow \left( 3x+1 \right) \left( 2x-5 \right) \le 0\\ \Rightarrow 6x^{ 2 }-13x-5\le 0\Rightarrow a=-13,b=-5\Rightarrow a+b=-18$ 故選(B)。

解：

$\begin{cases} 3^{ x+2 }-4^{ y }=17 \\ 3^{ x }+4^{ y-3 }=10 \end{cases}\Rightarrow \begin{cases} 9\cdot 3^{ x }-4^{ y }=17 \\ 3^{ x }+\frac { 1 }{ 64 } 4^{ y }=10 \end{cases}\Rightarrow \begin{cases} 3^{ x }=9 \\ 4^{ y }=64 \end{cases}\Rightarrow x=2,y=3$ 故選(D)。

解：

$4\log _{ 9 }{ 3 } +\log _{ 9 }{ 21 } -\log _{ 9 }{ 7 } =4\log _{ 9 }{ 3 } +\log _{ 9 }{ 3 } +\log _{ 9 }{ 7 } -\log _{ 9 }{ 7 } \\ =5\log _{ 9 }{ 3 } =5\times \frac { 1 }{ 2 } =\frac { 5 }{ 2 }$ ，故選(A)。

解：

$\sum _{ k=1 }^{ 20 }{ \left[ k\left( k+3 \right) \right] } =\sum _{ k=1 }^{ 20 }{ \left[ k^{ 2 }+3k \right] } =\frac { 20\times 21\times 41 }{ 6 } +3\times 21\times 20\div 2\\ =2870+630=3500$ ，故選(C)。

解：
前10項的和=

$(a_1+a_{10})\times 10 \div 2=(2+2+(-3)\times 9)\times 5 = -23\times 5=-115$ ，故選(B)。

解：
令1元硬幣有a個、5元硬幣有b個、10元硬幣有c個、50元硬幣有d個，此題相當於求
a+5b+10c+50d=100-1-5-10-50=34，其中a, b, c, d皆為大於等於零之整數。
又d一定等於0，即a+5b+10c=34
當c=3時, b=0
當c=2時, b=2,1,0
當c=1時, b=4,3,2,1,0
當c=0時, b=6,5,4,3,2,1,0
共有1+3+5+7=16組解，故選(A)。

解：
此題相當於甲+乙+丙=8，其中甲、乙、丙皆為大於等於0之整數，因此共有

$H^3_8=C^{10}_8 = 45$ ，故選(D)。

解：

${ \left( 2x^{ 2 }-\frac { 1 }{ x } \right) }^{ 9 }=\sum _{ n=0 }^{ 9 }{ C^{ 9 }_{ n }(2x^{ 2 })^{ n } } \left( -\frac { 1 }{ x } \right) ^{ 9-n }=\sum _{ n=0 }^{ 9 }{ C^{ 9 }_{ n }\cdot { 2 }^{ n }\cdot x^{ 2n } } \cdot \left( -1 \right) ^{ 9-n }\cdot x^{ n-9 }\\ =\sum _{ n=0 }^{ 9 }{ C^{ 9 }_{ n }\cdot { 2 }^{ n }\cdot \left( -1 \right) ^{ 9-n }\cdot x^{ 3n-9 } }$ 當n=3時，x次方為零，其係數為

$C^{ 9 }_{ 3 }\cdot { 2 }^{ 3 }\cdot \left( -1 \right) ^{ 6 }=84\times 8$ =672，故選(C)。

解：

A={2, 3, 5} B={2, 4, 6} , 積事件=交集，即 A

$\cap$ B={2}，故選(A)。

解：標準差=

$\sqrt { E\left( { X }^{ 2 } \right) -{ \left( EX \right) }^{ 2 } } =\sqrt { \frac { 200 }{ 8 } -{ \left( \frac { 32 }{ 8 } \right) }^{ 2 } } =\sqrt { 25-16 } =3$ ，故選(C)。

解：

$\sin { \theta } =\frac { 3 }{ 5 } \Rightarrow \cos { \theta } +\tan { \theta } =\frac { 4 }{ 5 } +\frac { 3 }{ 4 } =\frac { 31 }{ 20 }$ ，故選(C)。

解：

$\triangle ABE$ 三內角分別為

$360^\circ -60^\circ -90^\circ$ ，因此

$\overline{AE}=\overline{AB}\times \frac{\sqrt{3}}{ 2}=\frac{3\sqrt{3}}{2}$ 及

$\overline{EB}=\overline{AB}\times \frac{1}{2}=\frac{3}{2}$ 。
在直角

$\triangle AEC$ 中，

${\overline{AC}}^2= {\overline{AE}}^2+{\overline{CE}}^2 = \left( \frac{3\sqrt{3}}{2}\right)^2 + \left(6+\frac{3}{2}\right)^2=\frac{27}{4}+\frac{225}{4}$
= 64

$\Rightarrow \overline{AC}=\sqrt{63}=3\sqrt{7}$ ，故選(D)。

(A)7 (B)9 (C)11 (D)13
解：

${ \left( x+3 \right) }^{ 2 }+{ \left( y-4 \right) }^{ 2 }=4\Rightarrow \begin{cases} x=2\cos { \theta } -3 \\ y=2\sin { \theta } +4 \end{cases}\Rightarrow x^{ 2 }+y^{ 2 }={ \left( 2\cos { \theta } -3 \right) }^{ 2 }+{ \left( 2\sin { \theta } +4 \right) }^{ 2 }\\ =4\cos ^{ 2 }{ \theta } -12\cos { \theta } +9+4\sin ^{ 2 }{ \theta } +16\sin { \theta } +16=29-12\cos { \theta } +16\sin { \theta } \\ =29-4\left( 3\cos { \theta } +4\sin { \theta } \right) =29-20\left( \frac { 3 }{ 5 } \cos { \theta } +\frac { 4 }{ 5 } \sin { \theta } \right) \\ =29-20\left( \sin { \alpha } \cos { \theta } +\cos { \alpha } \sin { \theta } \right) =29-20\sin { \left( \alpha +\theta \right) }$ 最小值為29-20=9，故選(B)。

17. 設

$t$ 為實數，而

$\vec{a}=(3,5)，\vec{b}=(1,2)$ ，試問

$\left|\vec{a}+t\vec{b}\right|$ 的最小值為多少？

$(A)\frac{1}{\sqrt{5}}\;(B)\frac{1}{\sqrt{3}}\;(C)\frac{1}{\sqrt{2}}\; (D)1$ ;

解：

$\left| \vec { a } -t\vec { b } \right| =\left| \left( 3,5 \right) -t\left( 1,2 \right) \right| =\left| \left( 3-t,5-2t \right) \right| =\sqrt { { \left( 3-t \right) }^{ 2 }+{ \left( 5-2t \right) }^{ 2 } } =\sqrt { 5t^{ 2 }-26t+34 } \\ \Rightarrow t=\frac { 13 }{ 5 } 有極小值\sqrt { 5\times \frac { 169 }{ 25 } -26\times \frac { 13 }{ 5 } +34 } =\sqrt { 34-\frac { 169 }{ 5 } } =\sqrt { \frac { 1 }{ 5 } }$ 故選(A)。

18. 已知

$\left|\vec{a}\right|=2，\left|\vec{b}\right|=5$ ，且

$\vec{a}$ 與

$\vec{b}$ 的夾角為

$60^\circ$ ，試問

$\left|\vec{a}-\vec{b}\right|$ 的值為多少？

$(A)\sqrt{13}\;(B)\sqrt{15}\;(C)\sqrt{17}\;(C)\sqrt{19}$

解：

${ \left| \vec { a } -\vec { b } \right| }^{ 2 }={ \left| \vec { a } \right| }^{ 2 }+{ \left| \vec { b } \right| }^{ 2 }-2\vec { a } \cdot \vec { b } ={ \left| \vec { a } \right| }^{ 2 }+{ \left| \vec { b } \right| }^{ 2 }-2\left| \vec { a } \right| \left| \vec { b } \right| \cos { 60° } \\ =4+25-2\times 2\times 5\times \frac { 1 }{ 2 } =29-10=19\Rightarrow \left| \vec { a } -\vec { b } \right| =\sqrt { 19 }$ 故選(D)。

解：

$5\times 7-6\times 6$ =35-36=-1，故選(B)。

20. 已知

$\vec{a}=(1,2,3)，\vec{b}=(3,4,5)$ ，試問由

$\vec{a}$ 與

$\vec{b}$ 所張成的平行四邊形面積為多少？

$(A)\sqrt{6}\quad (B)2\sqrt{6}\quad (C)3\sqrt{6}\quad (D)4\sqrt{6}$

解：

$A=\sqrt { { \left| \begin{matrix} 2 & 3 \\ 4 & 5 \end{matrix} \right| }^{ 2 }+{ \left| \begin{matrix} 3 & 1 \\ 5 & 3 \end{matrix} \right| }^{ 2 }+{ \left| \begin{matrix} 1 & 2 \\ 3 & 4 \end{matrix} \right| }^{ 2 } } =\sqrt { 4+16+4 } =2\sqrt { 6 }$ 故選(B)。

解：
利用柯西不等式：

$\left( { x }^{ 2 }+{ \left( \sqrt { 2 } y \right) }^{ 2 }+{ \left( \sqrt { 3 } z \right) }^{ 2 } \right) \left( 1^{ 2 }+\sqrt { 2 } ^{ 2 }+\sqrt { 3 } ^{ 2 } \right) \ge { \left( 1\cdot x+\sqrt { 2 } y\cdot \sqrt { 2 } +\sqrt { 3 } z\cdot \sqrt { 3 } \right) }^{ 2 }\\ \Rightarrow \left( x^{ 2 }+2y^{ 2 }+3z^{ 2 } \right) \left( 1+2+3 \right) \ge { \left( x+2y+3z \right) }^{ 2 }\Rightarrow 4\times 6\ge { \left( x+2y+3z \right) }^{ 2 }\\ \Rightarrow \sqrt { 24 } \ge x+2y+3z\Rightarrow 2\sqrt { 6 } \ge x+2y+3z$ 故選(B)。

解：
兩平行線的向量

$\vec{u}=(2,-3,4)$
L1上取一點A=(2,-1,-5)、L2上取一點B=(-1,-3,4)，則

$\vec{AB}=(-3,-2,9)$
令

$\vec{v}=\vec{u}\times\vec{AB}$ =(-19,-30,-13)，因此平面方程式可為19x+30y+13z=k
以A點代入，可得38-30-65=k，k=-57，故選(D)。

解：

$2\begin{vmatrix} 1 & 3 \\ 2 & 4 \end{vmatrix}+\begin{vmatrix} -1 & 7 \\ 0 & 2 \end{vmatrix}-\begin{vmatrix} 3 & 5 \\ -2 & 4 \end{vmatrix}=\begin{vmatrix} 2 & 6 \\ 4 & 8 \end{vmatrix}+\begin{vmatrix} -4 & 2 \\ 2 & -2 \end{vmatrix}=\begin{vmatrix} -2 & 8 \\ 6 & 6 \end{vmatrix}$ 故選(A)。

解：A=0

$\Rightarrow k(k-2)-3=0\Rightarrow k^2-2k-3=0\Rightarrow$ (k-3)(k+1)=0

$\Rightarrow$ k=3(k=-1不合, k為正實數)，故選(C)。

解：
拋物線方程式為

$(x-2)^2=4(y-1)\Rightarrow 頂點為(2,1)，焦距=1\Rightarrow$ 準線為 y=1-1=0，故選(A)。

解：

$\sum _{ k=1 }^{ \infty }{ \frac { { 2 }^{ k-1 } }{ { 3 }^{ k } } } =\frac { 1 }{ 3 } \sum _{ k=1 }^{ \infty }{ \frac { { 2 }^{ k-1 } }{ { 3 }^{ k-1 } } } =\frac { 1 }{ 3 } \times \frac { 1 }{ 1-\frac { 2 }{ 3 } } =\frac { 1 }{ 3 } \times 3=1$ 故選(B)。

解：

出現1次的機率為

$\frac{1}{6}\times\frac{5}{6}\times\frac{5}{6}\times 3 = \frac{75}{216}$ ；
出現2次的機率為

$\frac{1}{6}\times\frac{1}{6}\times\frac{5}{6}\times 3 = \frac{15}{216}$ ；
出現3次的機率為

$\frac{1}{6}\times\frac{1}{6}\times\frac{1}{6}\times 3 = \frac{1}{216}$ ；
期望值為

$\frac{75}{216}+ \frac{15}{216}\times 2+\frac{1}{216}\times 3 = \frac{108}{216}=\frac{1}{2}$ ，故選(D)。

解：
二紅二白共有

$C^4_2=6$ 種排法，每一種都是二白二紅，機率皆為

$\left(\frac{1}{3}\right)^2 \times\left(\frac{2}{3}\right)^2$ ，所以機率為

$6\times \frac{1}{9}\times\frac{4}{9}= \frac{24}{81} =\frac{8}{27}$ ，故選(C)。

解：

$x=\frac{-\pi}{4}\Rightarrow f(x)=2\cos(0)+3=5$ ，故選(C)。

解：

$\lim _{ x\rightarrow -3 }{ \frac { x^{ 2 }+4x+3 }{ x^{ 2 }+5x+6 } } =\lim _{ x\rightarrow -3 }{ \frac { (x+3)(x+1) }{ (x+3)(x+2) } } =\lim _{ x\rightarrow -3 }{ \frac { (x+1) }{ (x+2) } } =\frac { -2 }{ -1 } =2$ 故選(B)。

貳、多重選擇題

解：
(B) 若a=c 且b=d，則a-c=0=b-d，0沒有大於0，所以不正確
(C)3>1且-1>-3，-3沒有大於-3，所以不正確
(D)-1>-3, 1沒有大於9，所以不正確
故選(AE)。

解：
(B) 若f(x)=2(x-1)+5,則f(x)除以(2x-2)的餘式為5
(D)f(x)的餘式為1次多項式，不是常數
故選(ACE)。

解：
六個相異球取出兩個，共有

$C^6_2=15$ 種取法
(A)(白, 白), (白,黑)x6,(黑黑)x3，共有10種取去,機率為10/15=2/3
(B)(紅,白)x2, (紅,黑)x3，共有5種取去,機率為5/15=1/3
(C)全部減去(兩球至少有一球是白=(白,白), (白,紅)x2, (白,黑)x6)=1-9/15=2/5
(D)(白,紅)x2, (白,黑)x6，共有8種取去,機率為8/15
(E)(白,白)，共有1種取去,機率為1/15
故選(BD)。

解：

$(A)P\left( A' \right) =1-P(A)=\frac { 7 }{ 10 } \quad \\ (B)P(A\cup B)=P(A)+P(B)-P(A\cap B)\Rightarrow \frac { 3 }{ 5 } =\frac { 3 }{ 10 } +\frac { 2 }{ 5 } -P(A\cap B)\\ \Rightarrow P(A\cap B)=\frac { 3 }{ 10 } +\frac { 2 }{ 5 } -\frac { 3 }{ 5 } =\frac { 1 }{ 10 } \\ (C)P(A'\cap B')=1-P(A\cup B)=1-\frac { 3 }{ 5 } =\frac { 2 }{ 5 } \\ (D)P(A'\cup B)=1-P(A)+P(A\cap B)=1-\frac { 3 }{ 10 } +\frac { 1 }{ 10 } =\frac { 4 }{ 5 } \\ (E)P(A\cup B')=1-P(B)+P(A\cap B)=1-\frac { 2 }{ 5 } +\frac { 1 }{ 10 } =\frac { 7 }{ 10 }$ 故選(ACDE)。

解：

$(A)C^{ 7 }_{ 2 }=\frac { 7! }{ 2!5! } =C^{ 7 }_{ 5 }\quad (B)C^{ 1 }_{ 1 }-C^{ 2 }_{ 1 }+C^{ 3 }_{ 1 }-C^{ 4 }_{ 1 }+C^{ 5 }_{ 1 }-C^{ 6 }_{ 1 }=1-2+3-4+5-6=-3\\ (C)C^{ 1 }_{ 1 }+C^{ 2 }_{ 1 }+C^{ 3 }_{ 1 }+C^{ 4 }_{ 1 }+C^{ 5 }_{ 1 }+C^{ 6 }_{ 1 }=1+2+3+4+5+6=21\\ (D)C^{ 6 }_{ 0 }-C^{ 6 }_{ 1 }+C^{ 6 }_{ 2 }-C^{ 6 }_{ 3 }+C^{ 6 }_{ 4 }-C^{ 6 }_{ 5 }+C^{ 6 }_{ 6 }={ \left( 1-1 \right) }^{ 6 }=0\\ (E)C^{ 6 }_{ 0 }+C^{ 6 }_{ 1 }+C^{ 6 }_{ 2 }+C^{ 6 }_{ 3 }+C^{ 6 }_{ 4 }+C^{ 6 }_{ 5 }+C^{ 6 }_{ 6 }={ \left( 1+1 \right) }^{ 6 }=64$ 故選(ABD)。

解：
圓C:

$(x-1)^2+(y+2)^2=3^2\Rightarrow$ 圓心(1,-2)，半徑=3。
圓心到直線的距離小於等於3即表示直線和圓心有交點。

$(A)\left| \frac { 3-8+40 }{ 5 } \right| =6>3\quad (B)\left| \frac { 3-8+30 }{ 5 } \right| =5>3\\ (C)\left| \frac { 3-8+20 }{ 5 } \right| =3=3\quad (D)\left| \frac { 3-8+10 }{ 5 } \right| =1<3\\ (E)\left| \frac { 3-8 }{ 5 } \right| =1<3$ 故選(CDE)。

解：

$(A)\sqrt { 3^{ 2 }+4^{ 2 }+5^{ 2 } } =5\sqrt { 2 } \quad (B)z座標=5\\ (C)y座標=4\quad (D)\sqrt { 4^{ 2 }+5^{ 2 } } =\sqrt { 41 } \\ (E)\sqrt { 3^{ 2 }+4^{ 2 } } =5$ 故選(BE)。

解：

$\begin{vmatrix} a & c \\ b & d \end{vmatrix}=5\Rightarrow ad-bc=5\\ (A)\begin{vmatrix} a & b \\ c & d \end{vmatrix}=ad-bc=5\quad (B)\begin{vmatrix} b & d \\ a & c \end{vmatrix}=bc-ad=-5\\ (C)\begin{vmatrix} 3a & 3c \\ b & d \end{vmatrix}=3\begin{vmatrix} a & c \\ b & d \end{vmatrix}=15\quad (D)\begin{vmatrix} a+2b & c+2d \\ b & d \end{vmatrix}=\begin{vmatrix} a & c \\ b & d \end{vmatrix}=5\\ (E)\begin{vmatrix} a+2b & c+2d \\ b & d \end{vmatrix}=\begin{vmatrix} a & c \\ b & d \end{vmatrix}=5$ 故選(BD)。

解：

$(A)X=\begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix},Y=\begin{bmatrix} 0 & 1 \\ 1 & 1 \end{bmatrix}\Rightarrow XY=\begin{bmatrix} 1 & 2 \\ 0 & 1 \end{bmatrix},YX=\begin{bmatrix} 1 & 0 \\ 2 & 1 \end{bmatrix}\Rightarrow XY\neq YX\\ (D)X=\begin{bmatrix} 1 & 1 \\ 1 & 1 \end{bmatrix},Y=\begin{bmatrix} -1 & -1 \\ -1 & -1 \end{bmatrix}\Rightarrow X+Y=\begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix}\neq X^{ 2 }+2XY+Y^{ 2 }\\ (E)X=\begin{bmatrix} 1 & 1 \\ 1 & 1 \end{bmatrix},Y=\begin{bmatrix} -1 & -1 \\ -1 & -1 \end{bmatrix}\Rightarrow X\neq ,Y\neq 0,但XY=\begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix}$ ，故選(BC)。

解：
sin(2x+3)的最小值為-1, 最大值為1，所以f(x)的最小值為-1+4=3、最大值為1+4=5
sin(x)的週期為

$2\pi \Rightarrow$ sin(2x)的週期為

$\pi$ ，故選(AC)。

朱式幸福

網頁

2017年9月18日星期一

105年警專35期甲組數學科詳解

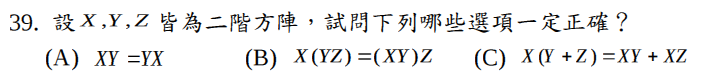
沒有留言:

張貼留言

網頁

2017年9月18日 星期一

105年 警專35期甲組數學科詳解

沒有留言:

張貼留言

2017年9月18日星期一

105年警專35期甲組數學科詳解