國立嘉義大學109學年度轉學生招生考試試題
科目：微積分 〈答案請寫在答案卷上〉
一、填充題：（每題 6 分，共 60 分）
解答：$$\lim_{x\to 0}{\int_0^x \left( 1+{t^2\over 4}- \sqrt[4]{1+t^2}\right)\,dx \over x^5} =\lim_{x\to 0}{ 1+{x^2\over 4}- \sqrt[4]{1+x^2} \over 5x^4} = \lim_{x\to 0}{ {x^2\over 2}- {1\over 4}(1+x^2)^{-3/4} (2x) \over 20x^3} \\=\lim_{x\to 0} {1-(1+x^2)^{-3/4} \over 40x^2} =\lim_{x\to 0} {{3\over 4}(1+x^2)^{-7/4}(2x) \over 80x }=\lim_{x\to 0} {3\over 160}(1+x^2)^{-7/4} =\bbox[red, 2pt]{3\over 160}$$
解答：$$\cases{f(2)=7\\ f(g(x))=x} \Rightarrow g(7)=2,又f(g(x))=x \Rightarrow f'(g(x))g'(x)=1 \Rightarrow g'(x)={1\over f'(g(x))} \\ \Rightarrow g'(7)= {1\over f'(g(7))} ={1\over f'(2)} =\bbox[red,2pt]{-{1\over 3}}$$
解答：$$\int_1^e 18x^2 \ln(x)\,dx = \left.\left[2x^3(3\ln x-1) \right] \right|_1^e =4e^3+2= a+be^3 \\ \Rightarrow \cases{a=2\\ b=4} \Rightarrow a+b= \bbox[red,2pt]6$$
解答：$$\int_{\pi/4}^{\pi/2} \cot^2(x) \,dx = \left.\left[-x-\cot(x) \right] \right|_{\pi/4}^{\pi/2} =-{\pi \over 2}-({\pi\over 4}-1)= 1-{1\over 4}\pi \\ \Rightarrow \cases{p=1\\ q=-1/4} \Rightarrow p+q = \bbox[red,2pt]{3\over 4}$$
解答：$$f(x)=\int_0^x \arctan(e^{3t})\,dt \Rightarrow f'(x)=\arctan(e^{3x}) \Rightarrow f''(x)= {1\over 1+e^{6x} }\cdot 3e^{3x} \Rightarrow f''(0)= \bbox[red, 2pt]{3\over 2}$$
解答：$$\lim_{x\to 2}{x^2+2x-8\over x^2-x-2} =\lim_{x\to 2}{(x+4)(x-2)\over (x-2)(x+1)} =\lim_{x\to 2}{x+4\over x+1} = \bbox[red, 2pt]2$$
解答：$$\int_0^2 |2x-1|\,dx =\int_0^{1/2} 1-2x \,dx +\int_{1/2}^2 2x-1\,dx =\left. \left[ x-x^2 \right] \right|_0^{1/2} +\left. \left[ x^2-x \right] \right|_{1/2}^2 \\ ={1\over 4}+{9\over 4} = \bbox[red,2pt]{5\over 2}$$
解答：$$x^3-3x^2y+ 2xy^2 =12 \Rightarrow 3x^2-6xy-3x^2y'+ 2y^2+4xyy'=0 \Rightarrow 3x^2-6xy+2y^2 = (3x^2-4xy)y' \\ \Rightarrow {dy\over dx} =y'=\bbox[red, 2pt]{3x^2-6xy+2y^2 \over 3x^2-4xy}$$
解答：$$取y=mx \Rightarrow \lim_{(x,y)\to (0,0)}{x+y \over x^2+y} =\lim_{x \to 0}{x(m+1) \over x(x+m)} =\lim_{x \to 0}{ m+1 \over x+m} ={m+1\over m}非定值\\ \Rightarrow \lim_{(x,y)\to (0,0)}{x+y \over x^2+y}\bbox[red, 2pt]{不存在}$$
解答：$$\int_0^\infty {1\over e^x+ e^{-x}}\,dx =\int_0^\infty {e^x\over e^{2x}+ 1}\,dx = \left. \left[ \arctan e^x\right] \right|_0^\infty ={\pi\over 2}-{\pi\over 4}= \bbox[red,2pt]{\pi\over 4}$$
二、計算題：（每題 10 分，共 40 分；請寫計算過程）
解答：$$x^2+y^2 =36 \Rightarrow 2x+2yy'=0 \Rightarrow y'=-{x\over y} \Rightarrow y''=-{1\over y}+{xy'\over y^2}=-{1\over y}+{x\over y^2}\cdot (-{x\over y}) \\=-{y^2+ x^2\over y^3}= \bbox[red,2pt]{-{36\over y^3}}$$
解答：$$a_n = {2^n\over n!} \Rightarrow L=\lim_{n\to \infty}\left| {a_{n+1}\over a_n }\right|=\lim_{n\to \infty} \left|{2^{n+1}\over (n+1)!} \cdot {n!\over 2^n} \right| =\lim_{n\to \infty} {2\over n+1} =0 \lt 1\\ 依比較級數審斂法\Rightarrow 該級數\bbox[red,2pt]{收斂}$$
解答：$$\cases{x=ts\\ y=s/t^2} \Rightarrow \cases{{\partial x\over \partial s}=t, {\partial x\over \partial t}=s \\ {\partial y\over \partial s}=1/t^2, {\partial y\over \partial t}= -2s/t^3} 又\cases{{\partial w\over \partial x}= f_x= x^2y =s^3\\ {\partial w\over \partial y}=f_y= y^2 = s^2/t^4} \\\Rightarrow \cases{{\partial w\over \partial s} ={\partial w\over \partial x}{\partial x\over \partial s} +{\partial w\over \partial y}{\partial y \over \partial s} =s^3t +s^2/t^6\\ {\partial w\over \partial t} ={\partial w\over \partial x}{\partial x\over \partial t} +{\partial w\over \partial y}{\partial y \over \partial t} =s^4-2s^3/t^7} \Rightarrow \cases{ {\partial w\over \partial s}\left. \right|_{(s,t)=(-1,1)} =-1+1= \bbox[red,2pt]0 \\{\partial w\over \partial t} \left. \right|_{(s,t)=(-1,1)} =1+2= \bbox[red,2pt]3}$$
解答：$$\cases{x=r\cos\theta \\ y=r\sin \theta } \Rightarrow \iint_D e^{-x^2-y^2}\,dA = \int_0^{2\pi} \int_0^2 re^{-r^2}\,drd\theta= \int_0^{2\pi} \left.\left[-{1\over 2}e^{-r^2} \right]\right|_0^2\,d\theta \\= \int_0^{2\pi} {1\over 2}(1-e^{-4})\,d\theta = \bbox[red,2pt]{\pi(1-e^{-4})}$$
==================== END =======================
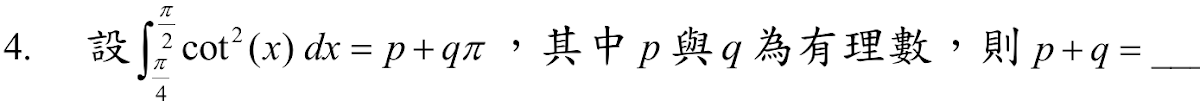
沒有留言:
張貼留言