113年南港高中教甄-數學詳解

 臺北市立南港高級中學 113 學年度第 1 次正式教師甄試 

(配分: 1~11 題 每題 8 分, 第 12 題 12 分.)

解答：$$f(x)=(x+1)^{100} =C^{100}_0+C^{100}_1x+ C^{100}_2 x^2+ \cdots +C^{100}_{100}x^{100} \\ \Rightarrow f'(x)=100(x+1)^{99} =C^{100}_1+2C^{100}_2x+ 3C^{100}_3x^2 +\cdots +100C^{100}_{100}x^{99} \\\qquad \qquad =C^{100}_{99} +2C^{100}_{98}x+ 3C^{100}_{97}x^2+ \cdots+100C^{100}_{0}x^{99} \\ \Rightarrow f'(1)=\bbox[red, 2pt]{100\cdot 2^{99}}=C^{100}_{99}+2C^{100}_{98}+3 C^{100}_{97}+ \cdots+ 100C^{100}_0$$

解答：$$\cases{R=(-{\pi\over 2},{\pi\over 2}) \\R_1=(-{\pi\over 2},-{\pi\over 3}]\\ R_2= [-{\pi \over 3}, -{\pi\over 6}] \\R_3=[-{\pi\over 6},0] \\R_4= [0,{\pi\over 6} ] \\R_5 [{\pi\over 6}, {\pi\over 3}] \\R_6=[{\pi\over 3},{\pi\over 2})} \Rightarrow R=R_1\cup R_2\cup R_3\cup R_4\cup R_5\cup R_6\\ \forall x \in \mathbb R, \exists \theta \in R_i,1\le i\le 6 \ni x=\tan^{-1} \theta. \text{For seven real numbers, there exists}\\ \text{two numbers }\cases{x=\tan^{-1}\theta_1\\ y =\tan^{-1} \theta_2}, \theta_1,\theta_2 \in R_i, 1\le i\le 6\\ \Rightarrow 0\le |\theta_1-\theta_2|\le {\pi\over 6} \Rightarrow 0\le \tan|\theta_1-\theta_2|\le \tan {\pi\over 6} \Rightarrow 0 \le {x-y\over 1+xy}\le {1\over \sqrt 3}. \bbox[red, 2pt]{QED}$$

解答：

由於四種餐點在五天中都要吃到，所以有一種餐點會吃兩次。因此我們可以假設四種情形：

甲：點2次A，其餘各1次，即AABCD來排列。但A、A、B三者不相鄰，只能排成A○A○B，C與D只能排在○的位置。AAB有3種排法，CD有2種排法，共有3X2=6種排法；

乙：點2次B，此情形與甲相同，共有6種排法。

丙：點2次C，其它ABD各一次。CCABD共有\({5!\over 2!}=60\)情形，但需扣除CC相鄰或AB相鄰。CC相鄰共有4!=24種情形，AB相鄰共有\({4!\over 2!}\times 2=24\)種情形，CC相鄰且AB相鄰共有\(3!\times 2 =12\)種情形。因此丙有60-24-24+12=24

丁：點2次D，此情形與丙相同，共有24種排法。

$$甲+乙+丙+丁=6+6+24+24= \bbox[red, 2pt]{60}$$

解答：

$$假設\cases{\overline{AQ} \bot \overline{CD} \\\overline{AB} \bot \overline{CP}\\ O為正方形BCDE中心點},由於\tan \theta={\sqrt{1-a^2}\over a},因此假設\cases{\overline{OQ}=a\\ \overline{AO}= \sqrt{1-a^2}} \Rightarrow \overline{AQ}=1\\ \Rightarrow \overline{AC} = \sqrt{1+a^2} \Rightarrow \overline{AB} =\overline{AC}= \sqrt{1+a^2} \Rightarrow \triangle ABC面積={1\over 2}\overline{AB}\cdot \overline{PC} = {1\over 2} \overline{CD}\cdot \overline{QA}\\ \Rightarrow\sqrt{1+a^2} \cdot \overline{PC} =2a\cdot 1 \Rightarrow \overline{PC}={2a\over \sqrt{1+a^2}} \Rightarrow \cos \alpha ={2\overline{PC}^2- \overline{EC}^2 \over 2\overline{PC}^2} =1-{ \overline{EC}^2 \over 2\overline{PC}^2} \\=1-{8a^2 \over {8a\over 1+a^2}}= \bbox[red, 2pt]{-a^2}$$

解答：$$m=3n \Rightarrow \sum_{k=1}^{3n} {k^2 \over 3n^3+k^3} = \sum_{k=1}^{m} {k^2 \over {1\over 9}m^3+k^3} = \sum_{k=1}^{m} {{1\over m}(k/m)^2 \over {1\over 9} +(k/m)^3}  \\ =\int_0^1 {x^2\over {1\over 9} +x^3} \,dx =\int_{1/9}^{10/9} {1/3\over u}\,du \; (u=1/9+x^3) =\left.\left [ {1\over 3}\ln u \right] \right|_{1/9}^{10/9} = \bbox[red, 2pt]{{1\over 3}\ln 10}$$ 

解答：$$\cases{D(0,0,0)\\ C(1,0,0)\\ A(0,1,0)\\ B(1,1,0)\\ E(0,1,1)\\ H(0,0,1)} \Rightarrow M\in \overline{BE} \Rightarrow M(1-t,1,t),0\le t\le 1 \\ \Rightarrow\cases{ \overline{AM}=\sqrt{2t^2-2t+1}\\ \overline{MH}=\sqrt{2t^2-4t+3}} \Rightarrow {\overline{AM}+ \overline{MH}\over 2} \ge \sqrt{\overline{AM}\cdot \overline{MH}} \\ \Rightarrow \overline{AM}\cdot \overline{MH}= \sqrt{4t^4-12t^3+16t^2-10t+3} =\sqrt{f(t)} \\ f'(t)=0 \Rightarrow {2t-1\over \sqrt{2t^2-2t+1}} +{2t-2\over \sqrt{2t^2-4t+3}}=0 \\ 2-{1\over 2t^2-2t+1} =2-{2\over 2t^2-4t+3} \Rightarrow 2t^2=1 \Rightarrow t={1\over \sqrt 2} \\ \Rightarrow \overline{AM}+ \overline{MH}=\sqrt{2-\sqrt 2}+\sqrt{4-2\sqrt 2} \Rightarrow (\overline{AM}+ \overline{MH})^2 =2+\sqrt 2 \Rightarrow \overline{AM}+ \overline{MH}=\bbox[red, 2pt]{2+\sqrt 2}$$

解答：

$$假設\triangle AIE的高為h,見上圖. 又\overline{AD}= \overline{DE} \Rightarrow \angle AED= \angle DAE=2\angle IAE=2\theta \\\triangle ADE三邊長為5,5,6 \Rightarrow \triangle ADE面積=\sqrt{8(8-5)(8-5)(8-6)} =12\\ \triangle ADE=\triangle AID+ \triangle AIE={1\over 2}\cdot 5h+{1\over 2}\cdot 6h={11h\over 2}=12 \Rightarrow h={24\over 11} \\ \cos \angle AED= \cos 2\theta={6^2+5^2-5^2\over 60}={3\over 5} \Rightarrow \sin \theta = \sqrt{1-\cos 2\theta \over 2} = \sqrt{1\over 5}\\ \overline{AI} \sin \theta =h \Rightarrow  \overline{AI}={h\over \sin \theta}=  \bbox[red, 2pt]{{24\over 11}  \sqrt 5}$$

解答：

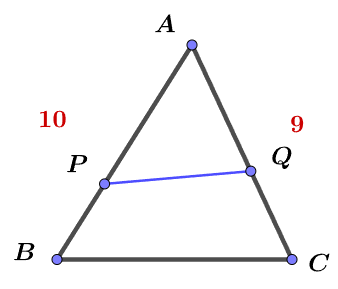
$$\frac{\triangle APQ}{\triangle ABC}=\frac{1}{2}\Rightarrow \frac{\overline{AP}\times\overline{AQ}} {\overline{AB}\times \overline{AC}}=\frac{1}{2}\Rightarrow \frac{\overline{AP}\times\overline{AQ}} {10\times 9}=\frac{1}{2} \Rightarrow \overline{AP}\times\overline{AQ}=45\\在\triangle APQ 中\Rightarrow \cos{\angle A}=\frac{\overline{AP}^2 +\overline{AQ}^2 -\overline{PQ}^2}{2 \overline{AP}\times\overline{AQ}} \Rightarrow \frac{3}{8}=\frac{\overline{AP}^2 +\overline{AQ}^2 -\overline{PQ}^2}{2\times 45}\\\Rightarrow \overline{AP}^2 +\overline{AQ}^2 -\overline{PQ}^2= \frac{135}{4} \Rightarrow \overline{PQ}=\sqrt{\overline{AP}^2 +\overline{AQ}^2 -\frac{135}{4}}\\ 由於\frac{\overline{AP}^2 +\overline{AQ}^2}{2} \ge \sqrt{\overline{AP}^2 \times \overline{AQ}^2}
=\overline{AP}\times\overline{AQ}=45 \Rightarrow \overline{AP}^2 +\overline{AQ}^2\ge 90\\ \Rightarrow \overline{PQ}=\sqrt{\overline{AP}^2 +\overline{AQ}^2 -\frac{135}{4}}\ge \sqrt{90-\frac{135}{4}}=\sqrt{\frac{225}{4}}=\bbox[red,2pt]{\frac{15}{2}}$$

解答：$$\cases{(a^2+b^2) (1^2+1^2) \ge (a+b)^2 \\ (b^2+c^2) (1^2+1^2) \ge (b+c)^2 \\(c^2+a^2) (1^2+1^2) \ge (c+a)^2 } \Rightarrow \cases {\sqrt{a^2+b^2} \ge (a+b)/\sqrt 2 \\\sqrt{b^2+c^2} \ge (b+c)/\sqrt 2 \\\sqrt{c^2+a^2} \ge (c+a)/\sqrt 2 }\\ \Rightarrow \sqrt{a^2+b^2}+ \sqrt{b^2+c^2}+ \sqrt{c^2+ a^2} \ge {2\over \sqrt 2}(a+b+c)= {2\over \sqrt 2}= \bbox[red, 2pt] {\sqrt 2}$$

解答：$$\cases{a_n= \sqrt 3a_{n-1} -b_{n-1} \\ b_n= a_{n-1}+ \sqrt 3b_{n-1}} \Rightarrow \begin{bmatrix}a_n \\ b_n \end{bmatrix} =\begin{bmatrix} \sqrt 3& -1\\ 1& \sqrt 3\end{bmatrix} \begin{bmatrix}a_{n-1} \\ b_{n-1} \end{bmatrix} \\ A= \begin{bmatrix} \sqrt 3& -1\\ 1& \sqrt 3\end{bmatrix} = 2\begin{bmatrix} \cos (\pi/6) & -\sin(\pi/6)\\ \sin (\pi/6)& \cos (\pi/6)\end{bmatrix} \Rightarrow A^{n}= 2^n \begin{bmatrix} \cos (n\pi/6) & -\sin(n\pi/6)\\ \sin (n\pi/6)& \cos (n\pi/6)\end{bmatrix} \\ \Rightarrow \begin{bmatrix}a_{18} \\ b_{18} \end{bmatrix} = A^{18} \begin{bmatrix}a_0 \\ b_0 \end{bmatrix} = 2^{18} \begin{bmatrix} \cos (3\pi) & -\sin(3\pi)\\ \sin (3\pi)& \cos (3\pi)\end{bmatrix} \begin{bmatrix} a_0 \\ b_0 \end{bmatrix} = 2^{18} \begin{bmatrix} -1 & 0\\ 0& -1\end{bmatrix} \begin{bmatrix} a_0 \\ b_0 \end{bmatrix}\\ =2^{18} \begin{bmatrix} -a_0 \\ -b_0 \end{bmatrix} \Rightarrow \cases{a_{18}=-2^{18}a_0 \\b_{18} =-2^{18} b_0} \Rightarrow a_{18}+b_{18}=-2^{18}(a_0+b_0)= \bbox[red, 2pt]{-2^{19}}$$

解答：

$$\text{Case I: }x\ge y \Rightarrow \cases{P(x,y)至右邊界(x=1)的距離\ge |x-y| \\ P(x,y)至下邊界(y=0)的距離\ge |x-y|} \Rightarrow \cases{1-x\ge x-y\\ y\ge x-y} \\ \qquad \Rightarrow \cases{2x-y\le 1\\ 2y\ge x}\\\text{Case II: }x\le y \Rightarrow \cases{P(x,y)至左邊界(x=0)的距離\ge |x-y| \\ P(x,y)至上邊界(y=1)的距離\ge |x-y|} \Rightarrow \cases{x\ge y-x\\ 1-y\ge y-x} \\\qquad \Rightarrow \cases{2x\ge y\\ 2y-x\le 1}\\四條直線所圍菱形如上圖,其中\cases{P= (y=2x)\cap (2y-x=1) =({1\over 3},{2\over 3})\\ Q=(x=2y)\cap (2x-y=1) =({2\over 3},{1\over 3})}\\ 因此\cases{兩平行直線距離={1\over \sqrt 5} \\ \overline{PB}={\sqrt 5\over 3}} \Rightarrow 菱形面積={1\over \sqrt 5}\times {\sqrt 5\over 3} =\bbox[red, 2pt]{1\over 3}$$

解答：$$\textbf{(1)}\; 轉換矩陣A=\begin{bmatrix}\frac{1}{4} & \frac{1}{4} & 0 & \frac{1}{4} & \frac{1}{5} \\ \frac{1}{4} & \frac{1}{4} & \frac{1}{4} & 0 & \frac{1}{5} \\ 0 & \frac{1}{4} & \frac{1}{4} & \frac{1}{4} & \frac{1}{5} \\\frac{1}{4} & 0 & \frac{1}{4} & \frac{1}{4} & \frac{1}{5} \\\frac{1}{4} & \frac{1}{4} & \frac{1}{4} & \frac{1}{4} & \frac{1}{5} \end{bmatrix} \Rightarrow A^2= \begin{bmatrix} \frac{19}{80} & \frac{7}{40} & \frac{7}{40} & \frac{7}{40} & \frac{19}{100} \\ \frac{7}{40} & \frac{19}{80} & \frac{7}{40} & \frac{7}{40} & \frac{19}{100} \\
\frac{7}{40} & \frac{7}{40} & \frac{19}{80} & \frac{7}{40} & \frac{19}{100} \\\frac{7}{40} & \frac{7}{40} & \frac{7}{40} & \frac{19}{80} & \frac{19}{100} \\\frac{19}{80} & \frac{19}{80} & \frac{19}{80} & \frac{19}{80} & \frac{6}{25} \end{bmatrix} \\ \Rightarrow A^2 \begin{bmatrix}0 \\ 0 \\0 \\0 \\ 1 \end{bmatrix} =\begin{bmatrix} \frac{19}{100} \\ \frac{19}{100} \\ \frac{19}{100} \\\frac{19}{100} \\ \frac{6}{25} \end{bmatrix} \Rightarrow \bbox[red,2pt]{6\over 25} \\\textbf{(2)}\; A^{n-1}\begin{bmatrix}0 \\0\\ 0\\0 \\ 1 \end{bmatrix} =\begin{bmatrix}(1-f(n))/4 \\ (1-f(n))/4\\  (1-f(n))/4 \\(1-f(n))/4 \\ f(n) \end{bmatrix} \Rightarrow A^n \begin{bmatrix}0 \\0\\ 0\\0 \\ 1 \end{bmatrix}= \begin{bmatrix}(1-f(n+1))/4 \\ (1-f(n +1))/4\\  (1-f(n+1))/4 \\(1-f(n+1))/4 \\ f(n+1) \end{bmatrix} \\ \Rightarrow \begin{bmatrix}\frac{1}{4} & \frac{1}{4} & 0 & \frac{1}{4} & \frac{1}{5} \\ \frac{1}{4} & \frac{1}{4} & \frac{1}{4} & 0 & \frac{1}{5} \\ 0 & \frac{1}{4} & \frac{1}{4} & \frac{1}{4} & \frac{1}{5} \\\frac{1}{4} & 0 & \frac{1}{4} & \frac{1}{4} & \frac{1}{5} \\\frac{1}{4} & \frac{1}{4} & \frac{1}{4} & \frac{1}{4} & \frac{1}{5} \end{bmatrix} \begin{bmatrix}(1-f(n))/4 \\ (1-f(n))/4\\  (1-f(n))/4 \\(1-f(n))/4 \\ f(n) \end{bmatrix} = \begin{bmatrix}(1-f(n+1))/4 \\ (1-f(n +1))/4\\  (1-f(n+1))/4 \\(1-f(n+1))/4 \\ f(n+1) \end{bmatrix} \\ \Rightarrow f(n+1)={1\over 4}(1-f(n))+{1\over 5}f(n)=-{1\over 20}f(n)+{1\over 4} \Rightarrow (x,y)= \bbox[red, 2pt]{(-{1\over 20},{1\over 4})}$$

================ END =================

解題僅供參考，其他歷年試題及詳解