解:$$\sum _{ k=1 }^{ 5 }{ \left( 2k-1 \right) } =2\sum _{ k=1 }^{ 5 }{ k } -\sum _{ k=1 }^{ 5 }{ 1 } =2\times \frac { 5\times 6 }{ 2 } -5=25$$
故選\(\bbox[red,2pt]{(B)}\)
解:$$\log _{ 10 }{ \left( 1000x \right) } =\log _{ 10 }{ 1000 } +\log _{ 10 }{ x } =3+\frac { 1 }{ 3 } =\frac { 10 }{ 3 } $$
故選\(\bbox[red,2pt]{(D)}\)
解:$$2x^{ 3 }-5x^{ 2 }-8x+6=\left( 2x+3 \right) \left( x^{ 2 }+kx+2 \right) =2x^{ 3 }+(2k+3)x^{ 2 }+(4+3k)x+6\\ \Rightarrow \begin{cases} 2k+3=-5 \\ 4+3k=-8 \end{cases}\Rightarrow k=-4$$
故選\(\bbox[red,2pt]{(C)}\)
解:
令f(x)=\(x^{1025}+19\),則f(-1)=-1+19=18
故選\(\bbox[red,2pt]{(A)}\)
解:$$\frac { 1-i }{ 2+i } =\frac { \left( 1-i \right) \left( 2-i \right) }{ \left( 2+i \right) \left( 2-i \right) } =\frac { 1-3i }{ 5 } =a+bi\\ \Rightarrow \left( a,b \right) =\left( \frac { 1 }{ 5 } ,\frac { -3 }{ 5 } \right) $$
故選\(\bbox[red,2pt]{(C)}\)
解:
A、B為獨立事件,即P(A\(\cap\)B)=P(A)\(\times\)P(B)。
因此P(A\(\cup\)B)=P(A)+P(B)-P(A)✕P(B)⇒\(\frac{2}{3}=\frac{1}{2}+P(B)-\frac{1}{2}\times P(B)\)⇒P(B)=\(\frac{1}{3}\),故選\(\bbox[red,2pt]{(A)}\)
解:$$\begin{vmatrix} a & b \\ c & d \end{vmatrix}=\begin{vmatrix} 3a & 2b \\ 3c & 2d \end{vmatrix}=\begin{vmatrix} 3a+5b & 2b \\ 3c+5d & 2d \end{vmatrix}=\begin{vmatrix} 3a+5b & a+2b \\ 3c+5d & c+2d \end{vmatrix}$$
故選\(\bbox[red,2pt]{(A)}\)
解:$$令\frac { x-3 }{ 1 } =\frac { y-1 }{ 2 } =\frac { z }{ -1 } =t\Rightarrow x=t+3,y=2t+1,z=-t代入平面\\ \Rightarrow (t+3)+(2t+1)+(-t)=6\Rightarrow 2t=2\Rightarrow t=1\\ \Rightarrow (x,y,z)=(4,3,-1)=(a,b,c)\Rightarrow a+b+c=6$$
故選\(\bbox[red,2pt]{(A)}\)
解:
\(a_{10}=S_{10}-S_{9}=\frac{10}{11}-\frac{9}{10}=\frac{1}{110}\)
故選\(\bbox[red,2pt]{(C)}\)
解:
f(x)=\((x-3)^2+k-9\)⇒x=3時有最小值⇒x值離3越遠f(x)值越大⇒x=0有最大值f(0)=k=102
故選\(\bbox[red,2pt]{(B)}\)
解:$$\begin{bmatrix} 3 & 1 \\ 2 & k \end{bmatrix}\begin{bmatrix} 1 & 1 \\ 2 & 3 \end{bmatrix}=\begin{bmatrix} 1 & 1 \\ 2 & 3 \end{bmatrix}\begin{bmatrix} 3 & 1 \\ 2 & k \end{bmatrix}\Rightarrow \begin{bmatrix} 5 & 6 \\ 2k+2 & 3k+2 \end{bmatrix}=\begin{bmatrix} 5 & k+1 \\ 12 & 3k+2 \end{bmatrix}\Rightarrow k=5$$
故選\(\bbox[red,2pt]{(C)}\)
解:
若 n=100a+b,則\(n^k\)除以100的餘數與\(b^k\)除以100的餘數相同,
利用上述特性來計算n除以100的餘數。
\(11^{15}={11^3}^5=1331^5=(13\times 100+31)^5\),因此n除以100的餘數與\(31^5\)除以100的餘數相同;\(31^5=(31^2)^2\times 31=961^2\times 31\),此數除以100的餘數與\(61^2\times 31\)除以100的餘數相同;\(61^2\times 31 =3721\times 31\),此數除以100的餘數與\(21\times 31\) =651除以100的餘數相同,即51。
故選\(\bbox[red,2pt]{(D)}\)
解:
只有(A)及(D)的圓心座標為(-3,4),又圓心至Y軸的距離為3,故選\(\bbox[red,2pt]{(A)}\)
解:
令\(\vec{u}=(-1,3), \vec{v}=(2,-1)\),由餘弦定理\(\vec{u}\cdot\vec{v}= |\vec{u}||\vec{v}|\cos{\theta}\)⇒-5=\(5\sqrt{2}\cos{\theta}\)⇒\(\cos{\theta}=\frac{-1}{\sqrt{2}}\)
因此\(\theta=45^\circ或135^\circ\)。
故選\(\bbox[red,2pt]{(C)}\)
解:$$\frac { 1 }{ x } +\frac { 1 }{ y } =1\Rightarrow x+4y=\left( x+4y \right) \left( \frac { 1 }{ x } +\frac { 1 }{ y } \right) \\ =5+\left( \frac { x }{ y } +\frac { 4y }{ x } \right) \ge 5+\left( 2\times \sqrt { \frac { x }{ y } \times \frac { 4y }{ x } } \right) =5+4=9$$
故選\(\bbox[red,2pt]{(A)}\)
解:
$$\overrightarrow { GC } =\frac { 2 }{ 3 } \overrightarrow { DC } =\frac { 2 }{ 3 } \left( \overrightarrow { DA } +\overrightarrow { AC } \right) =\frac { 2 }{ 3 } \left( \frac { 1 }{ 2 } \overrightarrow { BA } +\overrightarrow { AC } \right) \\ =\frac { 2 }{ 3 } \left( \frac { -1 }{ 2 } \overrightarrow { AB } +\overrightarrow { AC } \right) =\frac { -1 }{ 3 } \overrightarrow { AB } +\frac { 2 }{ 3 } \overrightarrow { AC } $$
故選\(\bbox[red,2pt]{(B)}\)
解:$$\lim _{ x\rightarrow 1 }{ \frac { x-1 }{ \sqrt { x^{ 2 }+8 } -3 } } =\lim _{ x\rightarrow 1 }{ \frac { \left( x-1 \right) \left( \sqrt { x^{ 2 }+8 } +3 \right) }{ \left( \sqrt { x^{ 2 }+8 } -3 \right) \left( \sqrt { x^{ 2 }+8 } +3 \right) } } =\lim _{ x\rightarrow 1 }{ \frac { \left( x-1 \right) \left( \sqrt { x^{ 2 }+8 } +3 \right) }{ x^{ 2 }-1 } } \\ =\lim _{ x\rightarrow 1 }{ \frac { \left( x-1 \right) \left( \sqrt { x^{ 2 }+8 } +3 \right) }{ \left( x-1 \right) \left( x+1 \right) } } =\lim _{ x\rightarrow 1 }{ \frac { \left( \sqrt { x^{ 2 }+8 } +3 \right) }{ \left( x+1 \right) } } =\frac { 6 }{ 2 } =3$$
故選\(\bbox[red,2pt]{(B)}\)
解:$$\lim _{ x\rightarrow 1 }{ \frac { 3^{ n }+5^{ n+1 } }{ 4^{ n }+5^{ n } } } =\lim _{ x\rightarrow 1 }{ \frac { \left( \frac { 3 }{ 5 } \right) ^{ n }+\frac { 5^{ n+1 } }{ 5^{ n } } }{ \left( \frac { 4 }{ 5 } \right) ^{ n }+\left( \frac { 5 }{ 5 } \right) ^{ n } } } =\frac { 0+5 }{ 0+1 } =5$$
故選\(\bbox[red,2pt]{(D)}\)
解:
cosx (紅線)與sinx(綠線)有兩個交點,故選\(\bbox[red,2pt]{(C)}\)
解:
滿足條件的事件有
(1,2,3), (1,2,4), (1,2,5), (1,2,6), (1,3,4), (1,3,5), (1,3,6), (1,4,5), (1,4,6), (1,5,6)
(2,3,4), (2,3,5), (2,3,6), (2,4,5), (2,4,6), (2,5,6)
(3,4,5), (3,4,6), (3,5,6),
(4,5,6)
共20種,所以機率為\(\frac{20}{6\times 6\times 6}=\frac{5}{54}\)
故選\(\bbox[red,2pt]{(D)}\)
解:
三個正面的機率為\(\frac{1}{8}\)、2個正面的機率為\(\frac{3}{8}\)、1個正面的機率為\(\frac{3}{8}\),期望值為\(8\times\frac{1}{8}+3\times\frac{3}{8}+\frac{3}{8}=\frac{20}{8}\)。
三個反面的機率為\(\frac{1}{8}\),假設應賠x元,則\(x\times\frac{1}{8}=\frac{20}{8}\)⇒x=20,故選\(\bbox[red,2pt]{(D)}\)
解:
y軸與直線的交點為(0, -2),因此拋物線為開口向下,故選\(\bbox[red,2pt]{(A)}\)
解:
x趨近無窮大時,f(x)亦趨近無窮大,因此a>0;又f(x)的三個根中,其一為0,另二根皆為正值,因此f(x)=ax(x-m)(x-n),其中m, n均為正數。由此可知 b = -(m+n)<0, c=mn>0,故選\(\bbox[red,2pt]{(A)}\)
解:$$\left|\vec{a}\times\vec{b}\cdot\vec{c}\right| = \left|(-2,0,0)\times (-1,0,2) \cdot (-1,3,2)\right| =\left|(0,4,0)\cdot(-1,3,2)\right| =12$$
故選\(\bbox[red,2pt]{(C)}\)
解:$$\vec { a } \cdot \vec { b } =\left( 5,4 \right) \cdot \left( \cos { x } ,3\sin { x } \right) =5\cos { x } +12\sin { x } =13\left( \frac { 5 }{ 13 } \cos { x } +\frac { 12 }{ 13 } \sin { x } \right) \\ =13\left( \sin { y } \cos { x } +\cos { y } \sin { x } \right) =13\sin { \left( x+y \right) } $$
故選\(\bbox[red,2pt]{(C)}\)
解:$$S_{ n }=\frac { a_{ 1 }(1-r^{ n }) }{ 1-r } \Rightarrow \frac { S_{ 6 } }{ S_{ 3 } } =\frac { 1-r^{ 6 } }{ 1-r^{ 3 } } =\frac { 7 }{ 8 } \Rightarrow 8r^{ 6 }-7r^{ 3 }-1=0\\ \Rightarrow \left( 8r^{ 3 }+1 \right) \left( r^{ 3 }-1 \right) =0\Rightarrow r=\frac { -1 }{ 2 } \\ (若r=1,\frac { S_{ 6 } }{ S_{ 3 } } =\frac { 6a_{ 1 } }{ 3a_{ 1 } } =2\neq \frac { 7 }{ 8 } 因此r=1不合)\Rightarrow a_{ 6 }=2\times { \left( \frac { -1 }{ 2 } \right) }^{ 5 }=\frac { -1 }{ 16 } $$
故選\(\bbox[red,2pt]{(B)}\)
解:
故選\(\bbox[red,2pt]{(B)}\)
解:$$\overline { PQ } =\sqrt { { \left( \cos { \alpha } -\cos { \beta } \right) }^{ 2 }+{ \left( \sin { \alpha } -\sin { \beta } \right) }^{ 2 } } \\ =\sqrt { \cos ^{ 2 }{ \alpha } -2\cos { \alpha } \cos { \beta } +\cos ^{ 2 }{ \beta } +\sin ^{ 2 }{ \alpha } -2\sin { \alpha } \sin { \beta } +\sin ^{ 2 }{ \beta } } \\ =\sqrt { \left( \cos ^{ 2 }{ \alpha } +\sin ^{ 2 }{ \alpha } \right) +\left( \cos ^{ 2 }{ \beta } +\sin ^{ 2 }{ \beta } \right) -2\left( \cos { \alpha } \cos { \beta } +\sin { \alpha } \sin { \beta } \right) } \\ =\sqrt { 1+1-2\cos { \left( \alpha -\beta \right) } } =\sqrt { 2+2\times \frac { \sqrt { 2 } }{ 2 } } =\sqrt { 2+\sqrt { 2 } } $$
故選\(\bbox[red,2pt]{(B)}\)
解:$$\omega =\cos { \frac { \pi }{ 3 } } +i\sin { \frac { \pi }{ 3 } } =\frac { 1 }{ 2 } +\frac { \sqrt { 3 } }{ 2 } i\\ \left( A \right) \omega \left( \cos { \frac { \pi }{ 6 } } +i\sin { \frac { \pi }{ 6 } } \right) =\left( \frac { 1 }{ 2 } +\frac { \sqrt { 3 } }{ 2 } i \right) \left( \frac { \sqrt { 3 } }{ 2 } +\frac { 1 }{ 2 } i \right) =i\\ \left( B \right) \omega \left( \cos { \frac { \pi }{ 3 } } +i\sin { \frac { \pi }{ 3 } } \right) =\left( \frac { 1 }{ 2 } +\frac { \sqrt { 3 } }{ 2 } i \right) \left( \frac { 1 }{ 2 } +\frac { \sqrt { 3 } }{ 2 } i \right) =\frac { -1 }{ 2 } +\frac { \sqrt { 3 } }{ 2 } i\\ \left( C \right) \omega \left( \cos { \frac { \pi }{ 2 } } +i\sin { \frac { \pi }{ 2 } } \right) =\left( \frac { 1 }{ 2 } +\frac { \sqrt { 3 } }{ 2 } i \right) \times i=-\frac { \sqrt { 3 } }{ 2 } +\frac { 1 }{ 2 } i\\ \left( D \right) \omega \left( \cos { \frac { 2\pi }{ 3 } } +i\sin { \frac { 2\pi }{ 3 } } \right) =\left( \frac { 1 }{ 2 } +\frac { \sqrt { 3 } }{ 2 } i \right) \left( \frac { -1 }{ 2 } +\frac { \sqrt { 3 } }{ 2 } i \right) =-1<0$$
故選\(\bbox[red,2pt]{(D)}\)
解:$${ \left( \frac { 3 }{ 2 } \right) }^{ n }>10000\Rightarrow \log { { \left( \frac { 3 }{ 2 } \right) }^{ n } } >\log { 10000 } \Rightarrow n\left( \log { 3 } -\log { 2 } \right) >4\\ \Rightarrow 0.1761n>4\Rightarrow n>\frac { 4 }{ 0.1761 } \approx 22.7\Rightarrow n=23$$
故選\(\bbox[red,2pt]{(D)}\)
解:
(A) 0 > -1 ⇒ \(0^2<(-1)^2\)
(E) \(\pi>\frac{\pi}{2}\Rightarrow \sin{\pi}=0<\sin{\frac{\pi}{2}}=1\)
故選\(\bbox[red,2pt]{(BCD)}\)
解:
兩虛根為共軛,即c=1, d=-2,因此\((x-1)^2=-4\Rightarrow x^2-2x+5=0\)。
利用長除法可求得另一因式為(x+2)=0,因此a=0, b=1,e=-2。
故選\(\bbox[red,2pt]{(ACE)}\)
解:
(D) \(\overline{AC}\bot\overline{BD}\Rightarrow \overrightarrow{AC} \cdot\overrightarrow{BD}=0\),平行四邊形對角線不一定互相垂直!
故選\(\bbox[red,2pt]{(ABCE)}\)
解:
(A) \(\overrightarrow{AB}=(-1-2,3-0,1-2) = (-3, 3, -1)\)
(B) \(\overrightarrow{AC}=(1-2,2-0,3-2) = (-1, 2, 1)\Rightarrow |\overrightarrow{AC}|= \sqrt{1+4+1} =\sqrt{6}\)
(C) (-3,3,-1)‧(-1,2,1) = 3+6-1 = 8
(D) \(\left( \begin{vmatrix} 3 & -1 \\ 2 & 1 \end{vmatrix},\begin{vmatrix} -1 & -3 \\ 1 & -1 \end{vmatrix},\begin{vmatrix} -3 & 3 \\ -1 & 2 \end{vmatrix} \right) =\left( 5,4,-3 \right) \)
(E) \(\frac { 1 }{ 2 } \left| \overrightarrow { AB } \times \overrightarrow { AC } \right| =\frac { 1 }{ 2 } \left| \left( 5,4-3 \right) \right| =\frac { 1 }{ 2 } \sqrt { 25+16+9 } =\frac { 5\sqrt { 2 } }{ 2 } \)
故選\(\bbox[red,2pt]{(ACE)}\)
解:$$\overrightarrow { AB } =\left( 2-1,1-(-1),-1-1 \right) =\left( 1,2,-2 \right) \\ \overline { AB } 方程式\frac { x-1 }{ 1 } =\frac { y+1 }{ 2 } =\frac { z-1 }{ -2 } \\ 平面E方程式(x-2)+2(y-1)-2(z+1)=0$$
(A) (6-2)+2(0-1)-2(0+1)=4-2-2=0
(D) \(\left| \frac { 6 }{ \sqrt { 1+4+4 } } \right| =2\)
(E)平面2x+z=0之法向量為(2,0,1)與E的法向量(1,2,-2)之內積為2-2=0,因此互垂。
故選\(\bbox[red,2pt]{(ADE)}\)
解:
(D)\(\sin{2\theta}=2\sin{\theta}\cos{\theta}=2\times\frac{3}{5}\times\frac{-4}{5}=\frac{-24}{25}\)
(E)\(180°>\theta >90°\Rightarrow 90°>\frac { \theta }{ 2 } >45°\Rightarrow \cos { \frac { \theta }{ 2 } } >0\)
故選\(\bbox[red,2pt]{(ABC)}\)
解:
(A) 50/5=10
(B) \(\sigma=\sqrt{EX^2-(EX)^2}=\sqrt{\frac{625}{5}-10^2}=\sqrt{125-100}=5\)
(C) E(3X-1)=3(EX)-1 = 30-1=29
(D) \(3\sigma=3\times 5=15\)
(E) \(\frac{12-\bar{x}}{5}=\frac{2}{5}\)
故選\(\bbox[red,2pt]{(ADE)}\)
解:
(A) (x-6)(x+1)<0⇒-1<x<6 (B) \((x-3)^2(x+2)<0\Rightarrow (x+2)<0\Rightarrow x<-2\)
(C) \(x^2(x-3)(x+2)<0 \Rightarrow (x-3)(x+2)<0\Rightarrow -2<x<3 (不含x=0)\)
(D) \((x^2+1)(x-3)(x+2)<0\Rightarrow (x-3)(x+2)<0\Rightarrow -2<x<3\)
(E) \(\frac{x+2}{x-3}\Rightarrow (x+2)(x-3)<0\Rightarrow -2<x<3\)
故選\(\bbox[red,2pt]{(DE)}\)
解:
(C)共軛雙曲線為\(\frac{y^2}{9}-\frac{x^2}{4}=1
(D) (0,0)是中心在漸近線上,所以沒有切線
(E) (2,3)在漸近線上且不是中心點, 因此只能有一條切線
故選\(\bbox[red,2pt]{(ABE)}\)
解:
|P| = 4-6=-2、|Q| = 1、|R|=-1、|S| = 1、|T|=(-9-16)/25=-1,行列式之絕對值為1者: QRST
故選\(\bbox[red,2pt]{(BCDE)}\)
-- END --







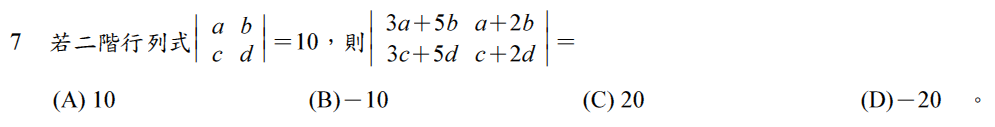








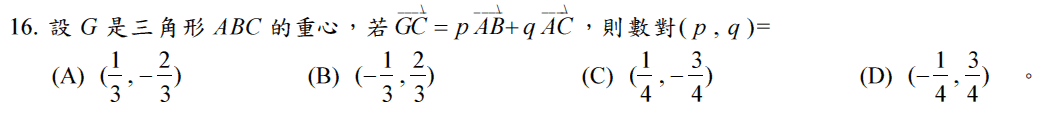





























沒有留言:
張貼留言