113年金門縣國中教甄聯招-數學詳解

金門縣113學年度國民中學正式教師聯合甄選

解答: $$三根之和=a+b+c=4 \Rightarrow \log_{1/2}(a+b+c)= \log_{1/2} 4=-2，故選\bbox[red, 2pt]{(D)}$$

解答: $$x^2+4x+3=x+k \Rightarrow x^2+3x+3-k=0 \\交點只有一個 \Rightarrow 判別式9-4(3-k)=0 \Rightarrow k={3\over 4} \Rightarrow x^2+3x+{9\over 4}=0 \\ \Rightarrow x=-{3\over 2} \Rightarrow y=x+k= -{3\over 2}+{3\over 4}=-{3\over 4} \Rightarrow 交點為 \left(-{3\over 2},-{3\over 4} \right)，故選\bbox[red, 2pt]{(C)}$$

解答: $${\cos{\pi\over 17} \cdot \cos{13\pi\over 17} \over \cos{3\pi\over 17} +\cos{5\pi\over 17}} = {1\over 2}\cdot {\cos{14\pi\over 17} + \cos{12\pi\over 17} \over \cos{3\pi\over 17} +\cos{5\pi\over 17}} = {1\over 2}\cdot {-\cos{3\pi\over 17} - \cos{15\pi\over 17} \over \cos{3\pi\over 17} +\cos{5\pi\over 17}} = -{1\over 2}，故選\bbox[red, 2pt]{(A)}$$

解答: $$f(k)=k^2 \Rightarrow (k+3)(k-2)+7=k^2 \Rightarrow k+1=0 \Rightarrow k=-1，故選\bbox[red, 2pt]{(C)}$$

解答: $$P在y=x^2上 \Rightarrow P(t,t^2),t\in \mathbb R \Rightarrow P至(0,1)的距離 =\sqrt{t^2+(t^2-1)^2} =\sqrt{t^4-t^2+1} \\=\sqrt{(t^2-{1\over 2})^2+{3\over 4}} \Rightarrow 當t^2={1\over 2}時,P至(0,1)的距離最近，此時\cases{P(1/\sqrt 2,1/2)\\ Q(-1/\sqrt 2, 1/2)} \\ \Rightarrow \overline{PQ}= \sqrt 2，故選\bbox[red, 2pt]{(B)}$$

解答: $$\cases{抽中白球的機率=11/35 \\抽中綠球的機率=6/35 } \Rightarrow {11\over 35}+{6\over 35} ={17\over 35}，故選\bbox[red, 2pt]{(C)}$$

解答: $$\sigma(X)=\sigma(X+50)= 25，故選\bbox[red, 2pt]{((B)}$$

解答: $$A=\begin{bmatrix}\cos 60^\circ & -\sin 60^\circ \\\sin 60^\circ & \cos 60^\circ \end{bmatrix} 為旋轉60度矩陣 \Rightarrow A^6=I，故選\bbox[red, 2pt]{(C)}$$

解答: $$f(\theta)={1+\tan \theta\over \sec \theta} \Rightarrow f'(\theta)={\sec^2 \theta\over \sec \theta}-{(1+\tan \theta)\sec \theta \tan  \theta\over \sec^2\theta } =\sec \theta-{(1+\tan \theta)\tan \theta \over \sec \theta} \\ \Rightarrow f'(\pi/4)=\sqrt 2-{2\over \sqrt 2} =0，故選\bbox[red, 2pt]{(A)}$$

解答: $$\int_{0}^8 \sqrt{x+1} \,dx =\int_1^9 \sqrt u\,du= \left. \left[ {2\over 3}u^{3/2} \right] \right|_1^9 ={2\over 3}(27-1)={52\over 3}，故選\bbox[red, 2pt]{(A)}$$

解答: $$\cases{A(1,7,1)\\ B(4,7,1)\\ C(1,7,5)} \Rightarrow \cases{\overline{AB}=3\\ \overline{BC}=5\\ \overline{CA}=4} \Rightarrow 內心坐標={5A+4B+3C\over 5+4+3}\\={1\over 12}\left(5+16+3,35+28+21,5+4+15 \right) ={1\over 12}(24,84,24)=(2,7,2)，故選\bbox[red, 2pt]{(B)}$$

解答: $$x+y+3i=-4+xyi \Rightarrow \cases{x+y=-4\\ xy=3} \Rightarrow x,y 為a^2+4a+3=0的兩根 \\ \Rightarrow (x,y)=(-3,-1),(-1,-3) \Rightarrow (\sqrt x-\sqrt y)^2=((\sqrt 3-1)i)^2 =-(4-2\sqrt 3)\\= -4+2\sqrt 3，故選\bbox[red, 2pt]{(D)}$$

解答: $$全部-六人同船=3^6-3=729-3=726，故選\bbox[red, 2pt]{(B)}$$

解答: $$\lim_{x \to 1} {x^2+2x-3\over x-1} =\lim_{x \to 1} { (x+3)(x-1)\over x-1} =\lim_{x \to 1}  (x+3)=4，故選\bbox[red, 2pt]{(D)}$$

解答: $${1\over 1\times 4}+{1\over 2\times 5}+{1\over 3\times 6}+\cdots + {1\over  n\times (n+3)} +\cdots \\={1\over 3}\left({1\over 1}-{1\over 4} +{1\over 2}-{1\over 5}+{1\over 3}-{1\over 6}+ {1\over 4}-{1\over 7}+ \cdots+ {1\over n}-{1\over n+3}+ \cdots\right) \\= {1\over 3} \left( {1\over 1}+{1\over 2}+ {1\over 3}\right) ={11\over 18}，故選\bbox[red, 2pt]{(B)}$$

解答:

$$兩圖形 \cases{y=x^3/2\\ y=2x} 交點\cases{A(0,0)\\ B(2,4) \\C(-2,-4)}且皆為奇函數,因此所圍面積\\=2 \int_0^2 (2x-{x^3\over 2})\,dx = 2\left. \left[ x^2-{1\over 8}x^4\right] \right|_0^2 =2\cdot 2=4，故選\bbox[red, 2pt]{(A)}$$

解答: $$f(x)=x^3+ax^2+bx-3 \Rightarrow f'(x)=3x^2+2ax+b =3(x-1)(x+2)=3x^2+3x-6\\ \Rightarrow \cases{a=3/2\\ b=-6} \Rightarrow a\times b=-9，故選\bbox[red, 2pt]{(A)}$$

解答: $$f(x)=x^2+x \Rightarrow f'(x)=2x+1 \Rightarrow 假設切點P(t,t^2+t) \Rightarrow  切線斜率2t+1={t^2+t-1\over t-1} \\ \Rightarrow t^2-2t=0 \Rightarrow \cases{t=0\\ t=2} \Rightarrow \cases{P(0,0)\\ P(2,6)} \Rightarrow \cases{切線\overline{PQ}方程式: x=y\\切線\overline{PQ}方程式:5x-y=4}，故選\bbox[red, 2pt]{(B)}$$

解答: $${x+1\over (x+1)+{1\over (x-1)+{1\over x+1}}} ={x+2\over x+3} \\\Rightarrow (x+1)(x+3)=(x+1)(x+2)+ {x+2\over (x-1)+{1\over x+1}} =(x+1)(x+2)+ {x+2\over  {x^2\over x+1}} \\ \Rightarrow x+3= ({1\over x^2}+1)(x+2) \Rightarrow x^2-x-2=0 \Rightarrow 兩根之和=1，故選\bbox[red, 2pt]{(A)}$$

解答: $$\cases{3x^2+2xy+y^2-2y-1=0 \cdots(1)\\ x^2+2xy-y+1=0 \cdots(2)} \Rightarrow 1=3x^2+2xy+y^2-2y=y-x^2-2xy \\ \Rightarrow 4x^2+4xy+y^2=3y \Rightarrow y={1\over 3}(2x+y)^2 代入(2) \Rightarrow (x-y)^2=3 \\\Rightarrow \cases{x=y-\sqrt 3  \Rightarrow (y-\sqrt 3)^2+2(y-\sqrt 3)y-y+1=0\Rightarrow 3y^2-(4\sqrt 3+1)y+4=0 \Rightarrow 有二解\\ x=y+\sqrt 3  \Rightarrow (y+\sqrt 3)^2+2(y+\sqrt 3)y-y+1=0 \Rightarrow 3y^2+(4\sqrt 3-1)y+4=0 \Rightarrow 無實數解}\\ \Rightarrow 有兩組解，故選\bbox[cyan, 2pt]{(C)}, 但公布的答案是\bbox[red, 2pt]{(A)}\\經電腦繪圖,兩圖形只有兩個交點,如下:$$

解答: $$(a+b\sqrt 5)^2=(1+\sqrt 5)(16+8\sqrt 5) \Rightarrow a^2+5b^2+2ab\sqrt 5=56+24 \sqrt 5\\ \Rightarrow \cases{a^2+5b^2=56 \\ ab=12} \Rightarrow a^4-56a^2+720=0 \Rightarrow (a^2-20)(a^2-36)=0 \\ \Rightarrow a^2=36\quad (a是有理數,a^2\ne 20) \Rightarrow \cases{a=6 \Rightarrow b=2\\ a=-6 \Rightarrow b=-2} \Rightarrow (a,b)=(6,2),(-6,-2)兩組解\\，故選\bbox[red, 2pt]{(B)}$$

解答: $$\left(\sqrt{2+\sqrt 3} -\sqrt{2-\sqrt 3} \right)^2 =4-2=2 \Rightarrow \left(\sqrt{2+\sqrt 3} -\sqrt{2-\sqrt 3} \right)^{12} =2^6=8^2 \\ \Rightarrow \log_8\left(\sqrt{2+\sqrt 3} -\sqrt{2-\sqrt 3} \right)^{12}= \log_8 8^2 =2，故選\bbox[red, 2pt]{(C)}$$

解答: $$\cases{\tan A=5/6\\ \cot B=11} \Rightarrow \cases{\sin A=5/\sqrt{61} \\ \cos A=6/\sqrt{61} \\ \sin B= {1/\sqrt{122}} \\ \cos B=11/\sqrt{122}} \Rightarrow \sin(A+B)= \sin A\cos B+ \sin B\cos A \\={55\over \sqrt{61}\cdot \sqrt{122}} +{6\over \sqrt{122} \cdot \sqrt{61}} ={1\over \sqrt 2} \Rightarrow A+B=45^\circ，故選\bbox[red, 2pt]{(C)}$$

解答: $$\sin\left( \sin^{-1}{4\over 5}+ \sin^{-1}{5\over 13}\right) ={4\over 5}\cdot {12\over 13}+{3\over 5}\cdot {5\over 13} ={63\over 65} \Rightarrow \cos\left( \sin^{-1}{4\over 5}+ \sin^{-1}{5\over 13}\right) ={16\over 65} \\ \Rightarrow \sin \left( \sin^{-1}{16\over 65} \right) =\cos \left( \sin^{-1}{4\over 5}+ \sin^{-1}{5\over 13} \right)   = {16\over 65} \Rightarrow \sin^{-1}{4\over 5}+ \sin^{-1}{5\over 13}+ \sin^{-1}{16\over 65} ={\pi\over 2}\\，故選\bbox[red, 2pt]{(A)}$$

解答: $$橢圓:(x-1)^2+4(y-{3\over 2})^2=4 \Rightarrow P(2\cos \theta+1, \sin \theta+{3\over 2}) \Rightarrow (2,2)為\overline{PQ}中點 \\\Rightarrow Q(-2\cos \theta+3,-\sin \theta+{5\over 2}) \Rightarrow (-2\cos \theta+2)^2+4(-\sin \theta+1)^2=4 \\ \Rightarrow \cos\theta+\sin \theta=1 \Rightarrow \theta={\pi\over 2},2\pi \Rightarrow \overline{PQ}斜率={2\sin \theta-1\over 4\cos \theta-2}=-{1\over 2}，故選\bbox[red, 2pt]{(C)}$$

解答: $$M\in L:x-y+2=0 \Rightarrow M(t,t+2) \\\Rightarrow \overline{MA}-\overline{MB}=f(t)=\sqrt{(t-2)^2+(t+3)^2} -\sqrt{(t+1)^2+ (t-3)^2} \\ \Rightarrow f'(t)=0 \Rightarrow {4t+2\over \sqrt{2t^2+2t+13}} ={4t-4\over \sqrt{2t^2-4t+10}} \Rightarrow 9t^2-66t+21=0 \\\Rightarrow (t-7)(9t-3)=0 \Rightarrow \cases{t=7 \Rightarrow M(7,9)\\ t=1/3 \Rightarrow M(1/3,7/3)=\overline{AB} \cap L\Rightarrow f(t)為 極小值} \\ \Rightarrow a+b=7+9=16，故選\bbox[red, 2pt]{(D)}$$

解答: $$x={1\over 2}(\sqrt{11}-3) \Rightarrow \cases{2x^2=10-3\sqrt{11} \\ 4x^4=199-60\sqrt{11}} \\ \Rightarrow x\cdot 4x^4+3\cdot 4x^4+x\cdot 2x^2+8\cdot 2x^2+10x+5 =(x+3)4x^4+(x+8)2x^2+19x+5 \\=(x+3)(199-60\sqrt{11})+ (x+8)(19-3\sqrt{11}) +10x+5= (219-63\sqrt{11})x+682-204\sqrt{11} \\={1\over 2}(219-63\sqrt{11})(\sqrt{11}-3)+ 682-204\sqrt{11} =7，故選\bbox[red, 2pt]{(D)}$$

解答: $$直接取c=0 \Rightarrow \cases{ab=-1\\ a-3b=2\sqrt 3} \Rightarrow \cases{a=\sqrt 3\\ b=-1/\sqrt 3} \Rightarrow ab+c=-1，故選\bbox[red, 2pt]{(B)}$$

解答: $$依題意公差1,假設首項a \Rightarrow a_n=a+n-1 \Rightarrow S=\sum_{i=1}^n a_i={(2a+n-1)n\over 2} =1000 \\ \Rightarrow (2a+n-1)n=2000 =2^45^3 \Rightarrow (2a+n-1) 與n必須是2,5的倍數\\ \Rightarrow \cases{a=28\\n=25} \Rightarrow {a_r \over a_1} ={52\over 28}= {13\over 7} \Rightarrow a+b=20，故選\bbox[red, 2pt]{(D)}$$

解答: $$t=a^x+a^{-x} \Rightarrow t^2=a^{2x}+a^{-2x}+2 \Rightarrow a^{2x}+a^{-2x}=t^2-2\\ 又a^{3x}+a^{-3x}=(a^x+a^{-x})(a^{2x}+a^{-2x}-1)=t(t^2-3)=18 \\ \Rightarrow t^3-3t-18=0 \Rightarrow (t-3)(t^2+3t+6)=0 \Rightarrow t=3  \Rightarrow a^{2x}+a^{-2x}=3^2-2=7，故選\bbox[red, 2pt]{(A)}$$

解答: $$\sqrt{12+\sqrt{128}} =\sqrt{12+ 2\sqrt{32}} = \sqrt 8+\sqrt 4= 2\sqrt 2+2 \Rightarrow \cases{x=4\\ y= 2\sqrt 2-2} \\ \Rightarrow \sqrt{y+2 +\sqrt{4y+y^2} \over y+2 -\sqrt{4y+y^2}} =\sqrt{2\sqrt 2 +\sqrt{4 } \over 2\sqrt 2 -\sqrt{4 }} =\sqrt{2\sqrt 2 +2 \over 2\sqrt 2 -2} =\sqrt{ 12+8\sqrt 2\over 4} =\sqrt{3+2\sqrt 2} \\=\sqrt 2+1，故選\bbox[red, 2pt]{(C)}$$

解答: $$\cos B={1\over 2}={2^2+6^2-\overline{AC}^2 \over 2\cdot 2\cdot 6} \Rightarrow \overline{AC}=2\sqrt 7 \\ \overline{BD}是 \angle 的角平分線 \Rightarrow {\overline{AD} \over \overline{DC}}={\overline{AB} \over \overline{BC}}={2\over 6} \Rightarrow \overline{AD}={\sqrt 7\over 2}\\ \Rightarrow \cos \angle ABD= \cos 30^\circ ={\sqrt 3\over 2}={2^2+\overline{BD}^2-{7\over 4} \over 4\overline{BD}} \Rightarrow \overline{BD}={3\sqrt 3\over 2} \approx 2.6，故選\bbox[red, 2pt]{(B)}$$

解答: $$\sum_{i=5}^{200} a_i =\sum_{i=5}^{200} \lfloor \log i \rfloor =\sum_{i=5}^{9} \lfloor \log i \rfloor  + \sum_{i=10}^{99} \lfloor \log i \rfloor +\sum_{i=100}^{200} \lfloor \log i \rfloor  \\=0+90\times 1+101\times 2=292，故\bbox[cyan,2pt]{無解}，公布的答案是\bbox[red, 2pt]{(D)}$$

解答: $$y={3-\sin x\over 2+\cos x} \Rightarrow 2y+y\cos x=3-\sin x \Rightarrow y\cos x+ \sin x=3-2y \\ \Rightarrow \sqrt{y+1} \sin(x+\alpha)=3-2y \Rightarrow \sin (x+\alpha)={3-2y\over \sqrt{y+1}} \\ \Rightarrow \left| {3-2y\over \sqrt{y+1}}  \right|\le 1 \Rightarrow 3y^2-12y+8\le 0 \Rightarrow (y-2)^2 \le {4\over 3} \Rightarrow 2-{2\over \sqrt 3}\le y\le 2+{2\over \sqrt 3}\\ \Rightarrow \cases{a=2+{2\over \sqrt 3}\\ b=2-{2\over \sqrt 3}} \Rightarrow a+b=4，故選\bbox[red, 2pt]{(A)}$$

解答: $$用\text{ Lagrange }算子來求: \\令F(a,b,c,\lambda,\mu)= b^2-4b+3-\lambda(a+2b+4c)-\mu(a^2+4b^2+16c^2-6) \\ \Rightarrow \cases{F_a=-\lambda-2a\mu=0\\ F_b=2b-4-2\lambda-8b\mu=0\\ F_c=-4\lambda-32\mu c=0} \Rightarrow \lambda=-2\mu a=-8\mu c \Rightarrow a=4c \\ \Rightarrow 4c+2b+4c=0 \Rightarrow c=-{1\over 4}b \Rightarrow \cases{a=-b\\ c=-b/4} \Rightarrow (-b)^2+4b^2+16(-b/4)^2=6 \Rightarrow b=\pm 1 \\\Rightarrow  \cases{b=1 \Rightarrow b^2-4b+3=0 \\ b=-1 \Rightarrow b^2-4b+3=8} \Rightarrow 最小值=0，故選\bbox[red, 2pt]{(B)}$$

解答: $$\cases{A(3,-1)\\ B(2,5)\\ C(-1,3)} \Rightarrow \cases{L_{AB}:6x+y=17\\ L_{BC}: -2x+3y=11\\ L_{AC}: x+y=2} \Rightarrow \triangle ABC面積={1\over 2}\begin{vmatrix}3& -1 & 1 \\2 & 5& 1\\ -1& 3& 1 \end{vmatrix} =10 \\ \Rightarrow \cases{S_{ \triangle MAB} =15/3\\ S_{ \triangle MBC} =10/3\\ S_{ \triangle MCA} =5/3 } \Rightarrow \cases{\begin{Vmatrix}3& -1 & 1 \\2 & 5& 1\\ x& y& 1 \end{Vmatrix} =|-6x-y+17|=10\\[1ex] \begin{Vmatrix}2& 5 & 1 \\-1 & 3& 1\\ x& y& 1 \end{Vmatrix} =|-2x+3y-11|=20/3 \\[1ex]\begin{Vmatrix}3& -1 & 1 \\-1 & 3& 1\\ x& y& 1 \end{Vmatrix} =|4x+4y-8|=10/3} \Rightarrow \cases{x=5/6\\ y=2} ，故選\bbox[red, 2pt]{(C)}$$

解答: $$\cases{|\vec a|=1,|\vec b|=2, |\vec c|=3\\ \vec a+\vec b+\vec c=0 } \Rightarrow \cases{\vec b=2\vec a\\ \vec c=-3\vec a}  \Rightarrow |2\vec a+3\vec b+5\vec c|= |2\vec a+6\vec a-15\vec a|=|-7\vec a|= 7\\，故選\bbox[red, 2pt]{(A)}$$

解答: $$\sqrt{(x-6)^2+5^2} +\sqrt{(x+2)^2+1} =\overline{PQ}+ \overline{PR}, 其中\cases{P(x,0)\\ Q(6,5)\\ R(-2,1)} \\ \Rightarrow R對稱x軸的對稱點R'(-2,-1) \Rightarrow L= \overleftrightarrow{QR'}:4y=3x+2 \Rightarrow P=L\cap x軸=P(-{2\over 3},0) \\ \Rightarrow s=\overline{QR'}=10 \Rightarrow 6r+s=-4+10=6，故選\bbox[red, 2pt]{(B)}$$

解答: $$\cases{x+ky=10-2k \cdots(1)\\ kx-y=10k \cdots(2)} \Rightarrow (1)\times k \Rightarrow kx+k^2y=10k-2k^2 \cdots(3)\\ 由(2) \Rightarrow kx=10k+y 代入(3) \Rightarrow 10k+y+k^2y=10k-2k^2 \Rightarrow y={-2k^2\over k^2+1} \\ \Rightarrow y=-2+{2\over k^2+1} 為整數 \Rightarrow k=0,\pm 1，有三種可能，故選\bbox[red, 2pt]{(C)}$$

解答: $$M=abcde, 其中\cases{a為萬位數字\\ b為千位數字\\ c為百位數字\\ d為十位數字\\ e為個位數字},需滿足1\le a\le 9, 0\le b,c,d,e\le 9 \\ \Rightarrow \cases{a=9 \Rightarrow H^4_3\\ a=8 \Rightarrow H^4_4\\ \cdots\\ a=3\Rightarrow H^4_9\\ a=2 \Rightarrow H^4_{10}-4 (b,c,d,e=10四種情形)\\ a=1 \Rightarrow H^4_{11}-4-12 (b,c,d,e=11, 或(10,1,0,0)排列數} \\ \Rightarrow 共有 \left(\sum_{k=3}^{11}H^4_k \right)-4-4-12 = \left({1\over 6}\sum_{k=3}^{11} (k+1)(k+2)(k+3) \right)-20 =1350-20=1330\\，故選\bbox[red, 2pt]{(A)}$$

解答: $$11^2=121 \Rightarrow 11^3=1210+121=1331 \xrightarrow{只考慮後三位}331 \Rightarrow 3310+331=3641\\ \Rightarrow 6410+641=7051 \Rightarrow 0510+051=561 \Rightarrow 5610+561=6171 \Rightarrow 1710+171=1881\\ \Rightarrow 8810+881=9691 \Rightarrow 6910+691=7601 \Rightarrow 601 \Rightarrow 6+0+1=7，故選\bbox[red, 2pt]{(C)}$$

解答: $${3\over 2+3}+{4\over 2+4}-{3+4\over 2+3+4} ={22\over 45} \Rightarrow b-a=45-22=23，故選\bbox[red, 2pt]{(B)}$$

解答:

$$\overline{BQ}為\angle B的角平分線 \Rightarrow {\overline{AB} \over \overline{BC}} ={\overline{AQ} \over \overline{QC}} \Rightarrow {3\over 5} ={2\over \overline{CQ}} \Rightarrow \overline{CQ}={10\over 3} \\ 同理可得\overline{BP}={9\over 5},\overline{AR}={48\over 31} \\ 又\overline{AP}為\angle A的角平分線 \Rightarrow \cos \angle BAP= \cos \angle CAP \Rightarrow {9+\overline{AP}^2-{81\over 25} \over 6\overline{AP}} ={{256\over 9}+\overline{AP}^2 -{256\over 25} \over {32\over 3}\overline{AP}} \\ \Rightarrow \overline{AP}={16\over 5}, 又{\overline{AM} \over \overline{MP}}={\overline{AB} \over \overline{BP}} ={3\over 9/5} ={15\over 9}\Rightarrow \overline{AM}={15\over 24}\cdot \overline{AP}= {15\over 24}\cdot{16\over 5}=2，故選\bbox[red, 2pt]{(C)}$$

解答:

$$假設\cases{\overline{AB}=1\\ \overline{BP}=a\\ \overline{DQ}=b}, 由於\angle PAQ=45^\circ \Rightarrow \overline{PQ}=a+b \; \href{https://zhidao.baidu.com/question/193097272.html}{參考資料} \\ {ABCD\over \triangle APQ}={5\over 2} \Rightarrow S_{\triangle APQ}={2\over 5} \Rightarrow S_{\triangle ABP}+ S_{\triangle ADQ}+ S_{\triangle PQC}= {3\over 5} \\ \Rightarrow {1\over 2}(a+b+(1-a)(1-b))={1\over 2}(1+ab)={3\over 5} \Rightarrow ab={1\over 5}\\ 又\overline{PQ}^2=\overline{PC}^2 +\overline{QC}^2 \Rightarrow (a+ b)^2=(1-a)^2+(1-b)^2 \Rightarrow 2ab=-2(a+b)+2 \\ \Rightarrow a+b=1-{1\over 5}={4\over 5} \Rightarrow {\overline{AB} \over \overline{PQ}}={1\over 4/5}={5\over 4}，故選\bbox[red, 2pt]{(B)}$$

解答:

$$\triangle ADF \cong \triangle ABE \;(RHS) \Rightarrow \overline{BE}=\overline{DF}=a \Rightarrow \overline{CE}=\overline{CF}= 1-a \\ \Rightarrow \cases{\overline{AE}^2= 1+a^2\\ \overline{EF}^2=2(1-a)^2} \Rightarrow \overline{AE}=\overline{EF} \Rightarrow 1+a^2 =2(1-a)^2 \Rightarrow a^2-4a+1=0 \\ \Rightarrow a=2-\sqrt 3 \;(a=2+\sqrt 3\gt 1不合) \Rightarrow \overline{AE}=\sqrt{1+a^2} =\sqrt{8-4\sqrt 3} =\sqrt{8-2\sqrt{12}} \\=\sqrt 6-\sqrt 2，故選\bbox[red, 2pt]{(B)}$$

解答:

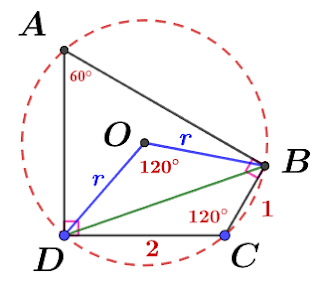
$$\angle B= \angle D=90^\circ \Rightarrow ABCD共圓，因此假設\cases{ 圓心O\\ 半徑r} \Rightarrow \angle C=180^\circ- \angle A=120^\circ\\ \triangle BCD: \cos \angle C={\overline{BC}^2+\overline{CD}^2-\overline{BD}^2 \over 2\cdot \overline{BC} \cdot \overline{CD}} \Rightarrow \overline{BD}=\sqrt 7\\ \triangle OBD: \cos \angle DOB=\cos (2\angle A) = {2r^2-\overline{BD}^2\over 2r^2} \Rightarrow r=\sqrt{7 \over 3} \\ \Rightarrow \overline{AC}=2r= 2\sqrt{7\over 3} \Rightarrow \overline{AC}^2={28\over 3} \Rightarrow a+b=28+3=31，故選\bbox[red, 2pt]{(D)}$$

解答: $$x={1\over \sqrt 2-1} =\sqrt 2+1 \Rightarrow \cases{a=2\\ b=\sqrt 2-1} \Rightarrow -x=-\sqrt 2-1 \Rightarrow \cases{c=-a-1\\ d=2-\sqrt 2} \\ \Rightarrow b^3+d^3+3bd=13-9\sqrt 2-12+9\sqrt 2=1，故選\bbox[red, 2pt]{(B)}$$

解答: $$\cases{\sum_{i=1}^8 a_i=56\\ \sum_{i=2}^7 a_i=44} \Rightarrow a_1 +a_8=12 \Rightarrow \cases{(a_1,a_8)=(1,11) \Rightarrow 在2-10挑6個數總和為44 \\ (a_1,a_8)=(2,10)  \Rightarrow 在3-9挑6個數總和為44 \\ (a_1,a_8)=(3,9) \times:4-8不足6個數} \\ \Rightarrow 1\lt 4\lt 6\lt 7\lt 8\lt 9\lt 10\lt 11 \Rightarrow \cases{a_2=4\\ a_7=10} \Rightarrow 2_2+a_7=18，故選\bbox[red, 2pt]{(A)}$$

解答: $$f(n)=a(2n+2)(2n+3)(2n+4) +b(2n+1)(2n+3)(2n+4) \\\qquad +c(2n+1)(2n+2)(2n+4)+ d(2n+1)(2n+2)(2n+3) =6 \\ \Rightarrow \cases{f(-1/2)=6a=6 \Rightarrow a=1\\ f(-1)=-2b=6 \Rightarrow b=-3 \\f(-3/2) =2c=6 \Rightarrow c=3\\ f(-2)=-6d=6 \Rightarrow d=-1}  \Rightarrow 2a+b+2c+d=2-3+6-1=4，故選\bbox[red, 2pt]{(C)}$$

解答: $$S=\sum_{i=1}^{10} x_i \le 13 \Rightarrow S=10,11,12,13 \\ \Rightarrow \cases{S=10 \Rightarrow 10個1 \Rightarrow 1種情形\\ S=11 \Rightarrow 9個1,1個2 \Rightarrow 10種情形\\ S=12 \Rightarrow \cases{9個1,1個3 \Rightarrow 10種情形 \\ 8個1,2個2 \Rightarrow 45種情形} \\ S=13 \Rightarrow \cases{9個1,1個4\Rightarrow 10種情形\\ 8個1,1個2,1個3\Rightarrow 90種情形 \\ 7個1,3個2 \Rightarrow 120種情形}} \Rightarrow 合計286，故選\bbox[red, 2pt]{(C)}$$

===================== END ========================